
Высшая математика
.pdf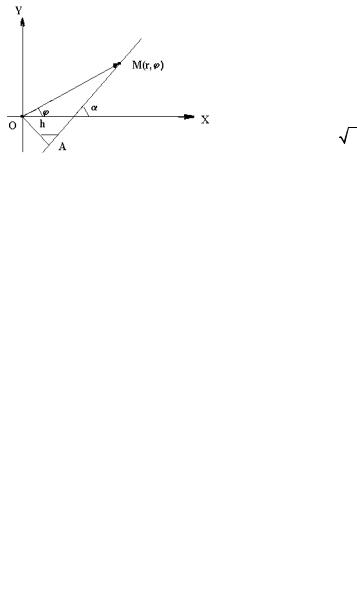
Пример 3. Найти полярные и прямоугольные декартовы координаты точки В, симметричной точке A(2; π 3) относительно полярной оси.
• Очевидно, что точка B(r; – ϕ) будет симметрична точке А(r; ϕ) относительно полярной оси. Поэтому, B(2; −π 3) – точка В в полярных координатах, т.е. r = 2,
ϕ = − |
π |
. Найдем декартовы координаты точки В по формулам (2): |
|||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
π |
|
− |
π |
|
= − |
3 . • |
|
|
x = 2 cos − |
= 1, |
y = 2 sin |
3 |
|
|||
|
|
|
3 |
|
|
|
|
|
|
Уравнением линии L в полярной системе координат называется уравнение |
|||||||||
вида |
F( r , ϕ ) = 0, если полярные координаты r |
и |
ϕ |
любой текущей точки |
|||||
M ( r ,ϕ ) линии L (и только они) удовлетворяют этому уравнению.
Уравнение может быть получено либо непосредственно, исходя из геометрических свойств линии, либо переходом к полярным координатам в уравнении этой линии, заданном в прямоугольных декартовых координатах.
Пример 4. Задано уравнение окружности в прямоугольной системе координат: ( x − 3 )2 + y2 = 9. Написать уравнение этой окружности в полярной системе координат, согласованной с декартовой системой.
• Вначале данное уравнение преобразуем: x2 + y2 = 6 x . Пользуясь формулами перехода от декартовых к полярным координатам ( x = r cosϕ, y = r sinϕ ) ,
получим уравнение окружности в полярной системе координат: r2 = 6r cosϕ r = 6 cosϕ . •
Пример 5. Вывести уравнение прямой в полярной системе координат.
• Если прямая L проходит через полюс и её угол наклона с полярной осью равен α ,
то уравнение этой прямой имеет вид tgϕ = tgα .
Пусть теперь прямая L не проходит через полюс, а отстоит от него на расстоянии h и имеет угол наклона α с полярной осью (рисунок 5).
Определяющее свойство произвольной (текущей) точки M ( r ,ϕ ) прямой L мож-
но
Рисунок 5 |
сформулировать так: |
|
uuur |
|
|
M ( r , ϕ ) L |
ПРuuur |
= const = h . |
|
|
OM |
|||
|
|
OA |
|
|
81
Т. к. |
AOM =90o |
+ϕ−α, |
uuur |
|
| OM |= r , то |
|
|||
|
uuur |
uuuur |
|
= −r sin(ϕ −α ) = r sin(α −ϕ ) = h . |
|
ПРuuurOM |
=| OM | cos( AOM ) |
||
|
OA |
|
|
|
Поэтому уравнение прямой можно записать в виде: r sin(α −ϕ ) = h . • |
||||
1.1.3 |
Параметрические уравнения линии |
|||
Иногда удобнее выразить текущие координаты точек линии через вспомогательный параметр t (время, угол и т. д.):
x = x( t )y = y( t ) .
В этом случае говорят, что линия задана параметрическими уравнениями. Имея уравнение линии в параметрической форме, иногда можно получить её
уравнение в виде F( x,y ) = 0, для этого нужно исключить параметр t. |
|
||||
Пример 6. Записать параметрические уравнения окружности радиуса |
R с |
||||
центром в точке M0 ( x0 ,y0 ). |
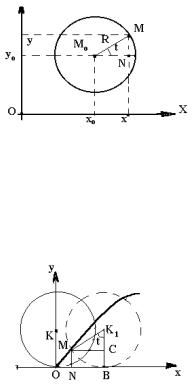
Пусть M(x, y) – текущая точка окружно- |
||||
|
• |
||||
|
сти. |
В качестве |
параметра |
возьмём |
угол |
|
t = MM0 N (рисунок 6). Тогда |
|
|||
|
|
x = x0 + Rcos t , |
|
|
|
|
|
y = y0 + R sint , 0 |
≤ t ≤ 2π |
(4) |
|
|
и есть параметрические уравнения окружности. |
||||
Рисунок 6 |
|
|
|
|
|
Исключим параметр t. |
|
|
x − x0 = Rcos t |
|
|
Для этого (4) запишем в виде |
y − y0 = R sint . |
|
|||
Возведём оба уравнения в квадрат и сложим: |
|
|
|
||
( x − x )2 + ( y − y )2 = R2 cos2 t + R2 sin2 t = R2 . |
|
|
|||
0 |
0 |
|
|
|
|
Получили уравнение окружности в виде: ( x − x0 )2 + ( y − y0 )2 = R2 . •
Пример 7. Вывести параметрические уравнения циклоиды, т.е. линии, которую описывает фиксированная точка окружности радиуса R, катящейся без скольжения по прямой линии.
• Окружность расположим так, чтобы фиксированная точка была в начале координат О. Пусть окружность катится вдоль положительного
82
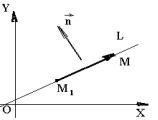
Рисунок 7 направления оси абсцисс. Точка K ( O,R ) окажется в точке K1 , а точка O( 0, 0 ) в точке M(x, y) (рисунок 7). Выразим координаты x и y через R и t = MK1B . Так как окружность катится без скольжения,
|
|
|
|
то OB = MB = Rt . Поэтому, |
|
|
|
x = ON = OB − NB = Rt − R sint = R( t − sint ), |
|
||
y = CB = K1B − K1C = R − Rcos t = R( 1 − cos t ). |
|
||
Окончательно, |
|
|
|
x = R( t − sint ) |
. |
(5) |
|
|
= R( 1 −cos t ) |
||
y |
|
|
|
Заметим, что уравнение этой линии после исключения параметра t приняло бы
|
|
y |
|
y |
|
|
|
довольно сложный вид: x = R arccos( 1 |
− |
|
) − sin(arccos( 1 − |
|
) . |
• |
|
R |
R |
||||||
|
|
|
|
|
1.2 Прямая линия
Прямая линия на плоскости является простейшей и наиболее употребительной из линий.
1.2.1 Уравнение прямой
Положение прямой L на плоскости OXY можно задать различными условиями. Рассмотрим несколько задач.
Задача 1. Пусть прямая L проходит через данную точку M1 ( x1 ,y1 ) перпен-
r |
|
|
|
|
|
дикулярно вектору n ={A,B} (вектор n называется нормальным). Найти урав- |
|||||
нение этой прямой. |
|
|
|
|
|
|
Возьмём на прямой L произвольную (теку- |
|
|||
|
щую) точку |
M( x,y ) и рассмотрим вектор |
|
||
|
uuuuur |
− x1 , y − y1} (рисунок 8). Так как |
|
||
|
M1 M ={x |
|
|||
|
uuuuur |
то |
r |
uuuuur |
|
|
M1 M || L , |
n |
M1 M . Поэтому скалярное |
||
|
|
r |
uuuuur |
|
|
|
произведение n M1 M = 0 . В координатной |
|
|||
|
форме имеем: |
|
|
|
|
Рисунок 8 |
A( x − x1 ) + B( y − y1 ) = 0 . |
(6) |
|||
Этому соотношению удовлетворяют координаты x и y любой точки M( x,y ) L , и только они. Из (6) следует, что
Ax + By + C = 0 , |
(7) |
83
где обозначено C = −Ax1 − By1 . Здесь А и В – координаты нормального вектора, x и y – текущие координаты, С – свободный член.
Соотношение (7) называется общим уравнением прямой на плоскости.
Итак, прямая может быть представлена уравнением первой степени относительно x и y.
Проанализируем уравнение (7).
1) Если А = 0, то n OX , L || OX . Уравнение прямой принимает вид
By + C = 0 или y = −C / B = const (горизонтальная прямая). При A = C = 0
уравнение y = 0 – уравнение оси OX.
2) |
Если В = 0, то n OY , L || OY . Уравнение прямой имеет вид |
|
|||||||||
Ax + C = 0 или x = − C / A = const |
(вертикальная прямая). При |
B = C = 0 |
|||||||||
уравнение x = 0 – уравнение оси OY. |
|
|
|||||||||
3) |
Пусть A ≠ 0, B ≠ 0 . Уравнение (7) запишем в виде |
|
|||||||||
|
|
y = − |
A |
x − |
C |
|
или y = kx + b , |
(8) |
|||
|
|
|
|||||||||
|
|
|
|
B B |
|
|
|||||
где обозначено k = − |
A |
, b = − |
C |
. |
|
|
|||||
|
|
|
|
||||||||
|
|
B |
|
|
B |
|
|
||||
Выясним геометрический смысл коэффициентов k и b. Для этого найдём точки пересечения прямой, задаваемой уравнением (8), с координатными осями.
При x = 0 y = b точка M1 ( 0; b ) . При y = 0 x = − kb точка
M2 ( − kb ; 0 ) . Рассмотрим угол наклона ϕ прямой, отсчитываемый от положи-
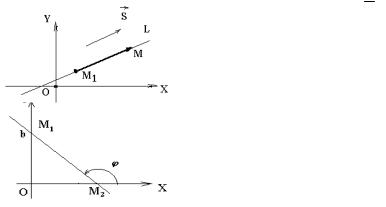
тельного направления оси OX против часовой стрелки до данной прямой. Ограничимся только случаем, рассмотренным на рисунке 9.
Рисунок 9 |
Рисунок 10 |
|
|
|
|||
tgϕ = tg(π − OM2 M1 ) = −tg( OM2 M1 |
) = − |
OM1 |
|
= − |
b |
= k . |
|
OM2 |
−b / k |
||||||
|
|
|
|
||||
Таким образом, k – угловой коэффициент прямой (тангенс угла наклона),
84
b – ордината точки пересечения прямой с осью OY .
Уравнение (8) называют уравнением прямой с угловым коэффициентом. Замечание. Уравнение прямой с заданным угловым коэффициентом и прохо-
дящей через данную точку M1 ( x1 ,y1 ) можно записать в виде |
|
y − y1 = k( x − x1 ) . |
(9) |
Задача 2. Пусть прямая L проходит через данную точку M1 ( x1 ,y1 ) парал- |
|||
r |
|
r |
|
лельно данному вектору S ={sx , sy } (вектор |
S называется направляющим век- |
||
тором прямой). Найдём уравнение этой прямой L. |
uuuuuur |
||
|
|
|
|
• Пусть точка M( x, y ) L – текущая точка прямой L. Тогда M1 M L и |
|||
uuuuur ur |
|
|
|
M1 M || S (определяющее свойство прямой L) (рисунок 10). |
|
||
По критерию коллинеарности векторов можно записать: |
|
||
uuuuur |
ur |
|
|
M1 M |
= t S , |
|
(10) |
где t – параметр. Получено параметрическое уравнение прямой в векторной форме. Это уравнение равносильно системе двух уравнений в координатной форме:
x − x |
1 |
= t s |
x |
|
|
x = x |
1 |
+ t s |
x |
|
|
|
|
|
или |
|
|
. |
(11) |
||||||
|
|
= t sy |
|
|
+ t sy |
|||||||
y − y1 |
|
|
y = y1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(параметрические уравнения прямой). |
|
|
|
|
|
|
|
|
||||
Параметрические уравнения прямой можно записать в виде |
|
|
||||||||||
|
|
x − x |
1 |
= t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
sx |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
y − y |
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
= t |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
sy |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
Исключая параметр t, получим каноническое уравнение прямой:
|
|
|
x − x1 |
= |
y − y1 |
. |
• |
(12) |
|||
|
|
|
sx |
|
|
||||||
|
|
|
|
|
sy |
|
|
||||
Задача 3. Положение прямой L можно задать двумя ее точками M1 ( x1 ,y1 ) |
|||||||||||
и M2 ( x2 ,y2 ) . Записать уравнение такой прямой. |
|
|
|||||||||
|
|
|
|
|
|
|
r |
|
|
||
• В этом случае за направляющий вектор S можно взять вектор |
|
||||||||||
uuuuuuur |
− x1 , y2 − y1} . Тогда каноническое уравнение прямой примет вид: |
||||||||||
M1 M2 ={x2 |
|||||||||||
|
|
x − x1 |
= |
|
y − y1 |
. |
• |
(13) |
|||
|
|
|
|
||||||||
|
|
x2 − x1 |
|
y2 − y1 |
|
|
|||||
Замечания.
85
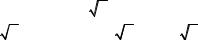
1. Каноническое уравнение прямой (12) можно представить в виде общего
уравнения прямой: sy x + ( −sx )y + ( sx y1 r− sy x1 ) = 0 . Заметим, что вектор nr ={sy , − sx } S ={sx ,sy } , т. к.
2. Одна из координат sx или sy направляющего вектора может быть равна ну-
лю. В этом случае уравнение прямой будет иметь вид x = x1 |
(если sx = 0 ) или |
|||||||||||||||||||
y = y1 (если sy = 0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 8. Написать общее уравнение прямой L, положение которой на плоско- |
||||||||||||||||||||
сти определяется следующими способами: |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
r |
{3, − 1} L ; |
|
|
||||||||
а) M1 ( 1, − 2 ) L , n = |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|||
б) M1 ( 2, 0 ) L , S ={1, 3} || L ; |
|
|
|
|||||||||||||||||
в) M1 ( 1, 1 ) L , M2 ( 0, − 1 ) L ; |
|
|
|
|||||||||||||||||
г) |
M1 ( −1, 1 ) L , |
( OX ,L ) = 120o ; |
|
|
||||||||||||||||
д) |
M1 ( 2, − 4 ) L , L L1 , L1 : 3x −5 y + 2 = 0 . |
|
||||||||||||||||||
• |
а) Согласно (6) получим: |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
3 ( x − 1 ) + ( −1 ) ( y − ( −2 )) = 0 3x − y − 5 = 0. |
|
|||||||||||||||||
б) Запишем каноническое уравнение прямой, используя (12): |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 2 |
= |
y −0 |
. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Получим общее уравнение: |
3( x − 2 ) = y 3x − y − 6 = 0 . |
|
||||||||||||||||||
Заметим, что прямые в случае а) и б) параллельны. |
|
|||||||||||||||||||
в) |
Воспользуемся (13): |
|
|
|
|
|
|
|
|
|
||||||||||
|
x − 1 |
= |
y − 1 |
|
|
x − 1 |
= |
y − 1 |
2( x − |
1 ) = y − 1 2 x − y − 1 = 0 . |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
0 − 1 |
−1 − 1 |
−1 |
−2 |
|
|
|
|||||||||||||
г) Так как ( OX ,L ) = 120o , то угловой коэффициент прямой |
||||||||||||||||||||
k = tg120o = tg( 90o + 30o ) = − ctg30o = − |
3 . Тогда, согласно (9), уравне- |
|||||||||||||||||||
ние прямой имеет вид |
y − 1 = − |
3 ( x − ( −1 )) 3x + y + |
3 − 1 = 0 . |
|||||||||||||||||
д) |
Вектор n ={3; −5} L1 , |
а, значит, n |
L , поэтому этот вектор можно |
|||||||||||||||||
взять в качестве направляющего вектора прямой L. Согласно (12), уравнение пря- |
||||||||||||||||||||
мой имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
x − 2 |
= |
y + 4 |
или 5 x + 3 y + 2 = 0 . • |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
−5 |
|
|
|
|
|
|
|
|
86
Вывод. Рассмотренные задачи показали, что как бы ни определять прямую линию на плоскости, ее уравнение будет уравнением первой степени
Ax + By + C = 0 , где A2 + B2 ≠ 0 .
Верно и обратное утверждение:
любое уравнение первой степени Ax + By + C = 0 задаёт прямую и только прямую на плоскости.
87
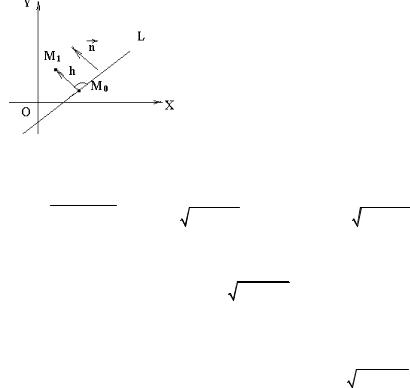
Для доказательства этого утверждения возьмём какое-нибудь конкретное решение ( x0 ,y0 ) рассматриваемого уравнения, тогда Ax0 + By0 + C = 0 . Так как
решений у уравнения Ax + By + C = 0 бесконечное множество, то для любого из них справедливо равенство
Ax + By + C − ( Ax0 + By0 + C ) = 0 A( x − x0 ) + B( y − y0 ) = 0 .
Левая часть этого равенства представляет скалярное произведение двух векто- |
||||||
r |
uuuuur |
r |
uuuuur |
|
r |
uuuuuur |
ров n ={A, B} и |
M0 M |
={x − x0 , y − y0 } . Так как n M0 M |
=0 |
n M0 M . |
||
А это означает, что все решения уравнения Ax + By + C = 0 определяют точки, лежащие на прямой, задаваемой вектором нормали n и точкой M0 .
1.2.2 Расстояние от точки до прямой
Задача 4. Найти расстояние h от точки M1 ( x1 ,y1 ) до прямой L, заданной
уравнением Ax + By + C = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
• Пусть точка M0 ( x0 , y0 ) L – проекция |
|
|||||||||||
|
|
|
|
|
|
|
точки M1 |
на прямую L (рисунок 11). Тогда |
|
||||||||||||
|
|
|
|
|
|
|
|
|
uuuuuuur |
={x1 − x0 , y1 − y0} |
r |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
M0 M1 |
|| n ={A,B} . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uuuuuuur r |
|
|
|
||
|
|
|
|
|
|
|
|
|
В этом случае | cos ( M0 M |
1 , n ) |= 1 , так |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
uuuuuuur |
|
|
|
или 180o . |
|||||
|
|
|
|
|
|
|
как угол между M0 M1 и n равен 0o |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
uuuuuuur |
r |
uuuuuuuur |
r |
|
|||||||
|
|
|
|
|
|
|
|
|
Поэтому, | M0 M1 |
n | =| M0 M1 | | n | . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
uuuuuur |
|
|
|
|
|
|
|||
|
Рисунок 11 |
|
|
|
|
Отсюда |
h =| M0 M1 |= |
|
|
|
|
|
|
||||||||
|
uuuuuuur |
r |
|
| A( x − x ) + B( y − y )| |
|
| Ax + By −( Ax + By )| |
|
||||||||||||||
|
| M |
M |
n | |
|
|
|
|||||||||||||||
= |
|
0 r1 |
|
= |
|
1 |
0 |
1 |
0 |
|
= |
|
|
1 |
1 |
0 |
0 |
|
. |
||
|
|
|
A2 + B2 |
|
|
|
|
A2 + B2 |
|
||||||||||||
|
|
| n | |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Так как M0 L Ax0 + By0 + C = 0 C = −( Ax0 + By0 ) . Итак, |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
h = |
| Ax1 + By1 + C | |
. |
|
|
|
|
(14) |
|||||||
|
|
|
|
|
|
|
|
A2 + B2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 9. Найти расстояние от прямой |
L : Ax + By + C = 0 до начала коор- |
||||||||||||||||||||
динат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| C | |
|
|
|
|
|
• Так как x1 = y1 = 0 , то, |
согласно (14), получим h = |
. • |
|
||||||||||||||||||
A2 + B2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
87

Пример 10. Найти расстояние между параллельными прямыми
L1 : Ax + By + C1 = 0 и L2 : Ax + By + C2 = 0 .
• Объясните, почему L1 || L2 . Очевидно, что расстояниеh между параллельными прямыми равно расстоянию от какой–либо точки M1 ( x1 ,y1 ) L1 до пря-
мой L |
: h = |
| Ax1 + By1 + C2 | |
= |
| −C1 + C2 | |
= |
| C1 − C2 | |
. • |
||
|
|
|
|||||||
2 |
|
A2 + B2 |
|
A2 + B2 |
A2 + B2 |
||||
|
|
|
|||||||
1.2.3 |
Взаимное расположение двух прямых |
|
|
||||||
Взаимное расположение двух прямых |
L1 |
и L2 |
на плоскости вполне определя- |
||||||
ется или их направляющими векторами |
ur |
uur |
|
|
|||||
S1 , S2 , или нормальными векторами |
|||||||||
n1 , nr2 , или угловыми коэффициентами k1 ,k2 . |
|
|
|||||||
Рассмотрим основную идею исследования взаимного расположения двух прямых для случая, когда прямые заданы своими общими уравнениями:
L1 : A1 x + B1 y + C1 = 0 ,
L2 : A2 x + B2 y + C2 = 0 .
Для этого выпишем векторы нормалей nr1 ={A1 , B1} и nr2 ={A2 , B2 }. Нетрудно заметить, что ( L1 ,L2 ) = ( n1 ,nr2 ) . Используя результаты из
векторной алгебры (глава 2), получим формулу, позволяющую находить угол меж-
ду прямыми: |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos ( L , L ) = |
|
rn1 n2r |
|
= |
|
|
A1 A2 + B1B2 |
|
. |
(15) |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
1 |
2 |
|
| n1 | | n2 |
| |
|
|
|
A12 + B12 A22 + B22 |
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
Отсюда легко получить условие перпендикулярности прямых L1 |
и L2 : |
|
|||||||||||||||||
|
|
r |
|
r |
r |
= 0 A1 A2 + B1B2 = 0 . |
|
(16) |
|||||||||||
L1 L2 n1 n2 |
n1 |
n2 |
|
||||||||||||||||
Условие параллельности прямых |
L1 |
|
и L2 следует из условия коллинеарности |
||||||||||||||||
их нормалей: |
|
|
|
|
|
|
|
|
|
|
A |
B |
|
|
|||||
|
|
|
|
|
r |
|
r |
|
|
|
|
||||||||
|
|
L || L n |
|| n |
|
|
1 |
|
= |
1 |
. |
|
|
(17) |
||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
2 |
1 |
|
2 |
|
|
A2 |
B2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Чтобы найти точку пересечения прямых L1 и L2 , необходимо и достаточно из |
|||||||||||||||||||
уравнений прямых составить систему и решить её: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
A x + B y + C |
1 |
= 0 , |
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
A2 x + B2 y + C2 = 0 . |
|
|
|
|
|
|
|||||||||||
Эта система будет иметь единственное решение |
( x0 , y0 ) , если L1 |
и L2 не |
|||||||||||||||||
88
параллельны, т.е. |
A1 |
≠ |
B1 |
A B |
2 |
− A B |
= |
A1 |
B1 |
≠ 0 . |
|
|
|
|
|||||||||
|
A2 |
|
B2 |
1 |
2 |
1 |
|
A2 |
B2 |
|
|
|
|
|
|
|
|
|
|
||||
Замечание. Если прямые заданы уравнениями в другой форме, то можно либо свести их к общим уравнениям и работать с векторами нормалей, либо использовать направляющие векторы или угловые коэффициенты.
Задача 5. Пусть даны две пересекающиеся прямые L1 и L2 с угловыми коэф-
фициентами k1 и k2 |
соответственно. Найти угол ϕ между L1 |
и L2 . |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
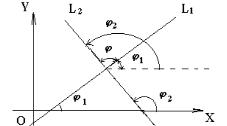
Из рисунка 12 видно, что ϕ =ϕ2 −ϕ1 . |
||||||||||||||
|
|
|
|
|
|
|
|
|
По известной формуле из тригонометрии |
||||||||||||||
|
|
|
|
|
|
|
|
|
tgϕ = tg(ϕ2 −ϕ1 ) = |
|
tgϕ2 − tgϕ1 |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 + tgϕ2 tgϕ1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Учитывая, |
что |
tgϕ1 = k1 , tgϕ2 = k2 , |
||||||||||||
|
|
|
|
|
|
|
|
|
получаем |
|
|
|
|
|
k2 − k1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
tgϕ = |
|
|
. (18) |
|||||||
|
Рисунок 12 |
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ k1 k2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Сформулируем два важных случая: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1) L1 || L2 ϕ1 =ϕ2 tgϕ1 = tgϕ2 k1 = k2 . |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
2) L |
L |
ϕ |
1 |
=ϕ |
2 |
± π |
tgϕ |
1 |
= −ctgϕ |
2 |
= − |
|
|
|
k |
1 |
= − |
1 |
, |
|
|||
|
|
|
|
|
|||||||||||||||||||
1 |
2 |
|
|
2 |
|
|
|
tgϕ2 |
|
|
|
|
|
k2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
т.е. у взаимно перпендикулярных двух прямых их угловые коэффициенты обратные по абсолютной величине и противоположные по знаку.
Пример 11. Выяснить, являются ли данные прямые L1 и L2 параллельными
или перпендикулярными. Если не выполняется ни то, ни другое, то найти угол между ними и точку пересечения.
а) |
L : x + 2 y − 3 = 0 и |
L : |
x + 1 |
= |
y |
; |
|
|
|||||
|
1 |
2 |
2 |
|
−1 |
|
|
|
|
|
|||
б) L1 : x = 6t − 1 , y = 2t + 1 и L2 : y = −3x + 2 ;
|
в) |
L : |
y − 1 |
= |
x |
и L : y = −3 x + 6 . |
|
||
|
|
|
|
||||||
|
|
1 |
2 |
|
1 |
2 |
|
||
|
|
|
|
|
|
||||
r |
• а) Прямая L1 |
задана общим уравнением, легко записать вектор нормали |
|||||||
={1; 2} . Прямая L2 задана каноническим уравнением, найдём направляющий |
|||||||||
n1 |
|||||||||
|
|
uur |
|
|
|
|
r |
ur |
|
вектор S2 ={2; − |
1} . Так как скалярное произведение n1 |
S2 =1 2 +2 ( −1 ) =0 , |
|||||||
|
r |
ur |
r |
L2 L1 || L2 . |
|
||||
то n1 |
S2 |
n1 |
|
||||||
89
