1. Операции над множествами.

2. Мощность конечного множества. Мощность объединения множеств. Мощность булеана.

3. Характеристическая функция множества. Свойства характеристических функций.

4. Характеристические векторы конечных множеств и их свойства.

5. Теоретико-множественные тождества. Методы доказательства тождеств.

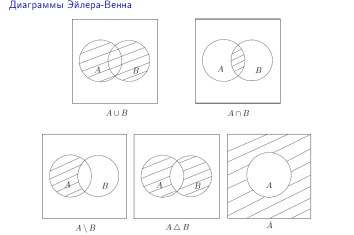
1) Операции над множествами.

À

2) Мощность конечного множества. Мощность объединения множеств. Мощность булеана.

3) Характеристическая функция множества. Свойства характеристических функций.

4) Характеристические векторы конечных множеств и их свойства.

5) Теорико-множественные тождества. Методы доказательства тождеств.

6. Декартово произведение множеств. Свойства декартового произведения.

7. Бинарные отношения. Основные определения.

8. Композиция бинарных отношений. Свойства композиции.

9. Свойства бинарных отношений.

10. Необходимое и достаточное условие симметричности бинарного отношения.

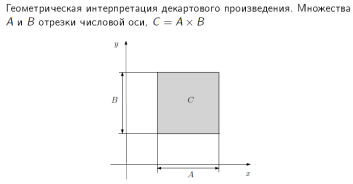
6) Декартово произведение множеств. Свойства декартового произведения.

7) Бинарные отношения. Основные определения.

8) Композиции бинарных отношений. Свойства композиции.

9) Свойства бинарных отношений.

10) Необходимое и достаточное условие симметричности бинарного отношения.

11. Необходимое и достаточное условие транзитивности бинарного отношения.

12. Необходимое и достаточное условие плотности транзитивного бинарного отношения.

13. Отношение эквивалентности. Классы эквивалентности. Теоремы о разбиении множества на классы эквивалентности.

14. Замыкания бинарных отношений. Теорема о замыканиях.

15. Теорема о транзитивном замыкании конечного множества.

11) Необходимое и достаточное условие транзитивности бинарного отношения.

12) Необходимое и достаточное условие плотности транзитивного бинарного отношения.

13) Отношение эквивалентности. Классы эквивалентности. Теоремы о разбиении множества на классы эквивалентности.

14) Замыкание бинарных отношений. Теоремы о замыканиях.

15) Теорема о транзитивном замыкании конечного множества.

16. Матрицы бинарных отношений и их свойства.

17. Отношение порядка. Упорядоченные множества. Диаграмма Хассе.

18. Отображения и функции.

19. Теорема о композиции биективных функций.

20. Перестановки, размещения, сочетания. Вывод формул для основных комбинаторных чисел.

16) Матрица бинарных отношений и их свойста.

17) Отношения порядка. Упорядоченные множества. Диаграмма Хассе.

18) Отображения и функции.

19) Теорема о композиции биективных функций.

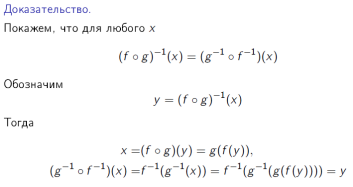
20) Перестановка, размещение, сочетания. Вывод формул для основных комбинаторных чисел.

21. Число разбиений конечного множества на подмножества.

22. Перестановки с повторениями.

23. Биноминальные коэффициенты и их свойства. Треугольник Паскаля.

24. Бином Ньютона.

25. Полиномиальная формула.

21) Число разбиений конечного множества на подмножества.

22) Перестановки с повторениями.

23) Биноминальные коэффициенты и их свойства. Треугольник Паскаля.

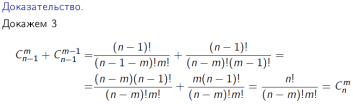
24) Бином Ньютона.

25) Полиноминальная формула.

26. Метод включений и исключений.

27. Число отображений: функций, биекций, сюръекций.

28. Булевы функции. Функции двух переменных. Фиктивные и существенные переменные.

29. Законы алгебры логики.

30. Классы булевых функций.

26) Метод включений и исключений.

27) Число отображений: функций, биекций, сюръекций.

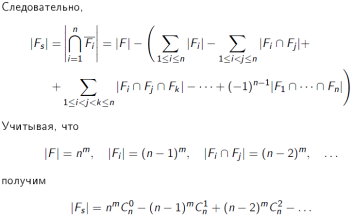
28) Булевы функции. Функции двух переменных. Фиктивные и существенные переменные.

29) Законы алгебры логики.

30) Классы булевых функций.

31. Замыкание множества булевых функций.

32. Функционально полные системы булевых функций. Теорема Поста.

33. Нормальные формы булевых функций.

34. Построение минимальной ДНФ методом Квайна.

35. Построение минимальной ДНФ методом карт Карно.

31. Замыкание множества булевых функций.

32. Функционально полные системы булевых функций. Теорема Поста.

33. Нормальные формы булевых функций.

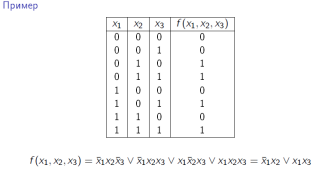
34. Построение минимальной ДНФ методом Квайна.

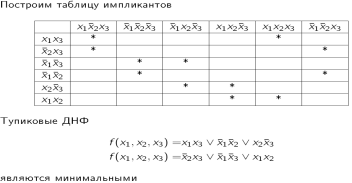
35. Построение минимальной ДНФ методом карт Карно.

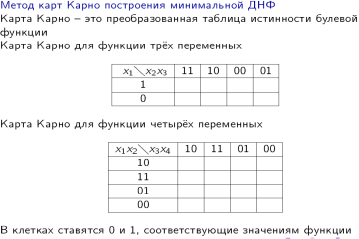
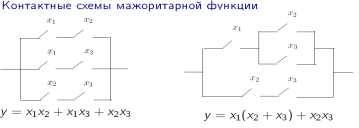
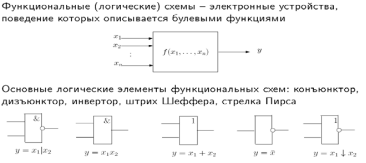
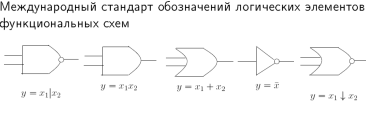
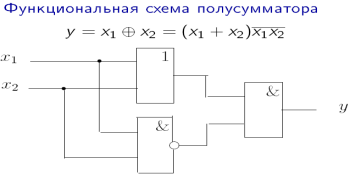
36. Контактные и функциональные схемы. Примеры.

37. Понятие алгебраической операции и алгебраической структуры.

38. Определение и свойства групп.

39. Группа подстановок.

40. Подгруппы. Пересечение подгрупп. Циклические подгруппы.

36. Контактные и функциональные схемы. Примеры.

37. Понятие алгебраической операции и алгебраической структуры.

Определение:отображение d:Aⁿ->A называется n-арной алгебраической операцией на множестве А

Определение: множество А с заданным на нем алгебраическими операциями 2,….α_n называется алгебраической структурой и обозначается

<A; α,,……, α_n>

Пример:множество действительных чисел, с операциями сложения и умножения образуют алгебраическую структуру <R;+,·>

Бинарную алгебраическую операцию будем обозначать: a*b, a+b,где а,b € A

Определение: Алгебраическая структура называется конечной, если число элементов конечно.

Конечную алгебраическую структуру <А,*> ,A={a_1,…..a_n}с бинарной операцией *

Можно задать таблицей Кэли:

*	a1	·	·	·	an
a1	b11	·	·	·	b1n
·		·			·
·			·		·
·				·	·
an	bn1	·	·	·	bnn

Где b_ij€ A

Пример А={0;1;2}, a+b mod3

+	0	1	2
0	0	1	2
1	1	2	0
2	2	0	1

Определение:Алгебраическая операция называется Коммунитативной, если ab=ba .Называется Ассоциативной, если (ab)c=a(bc)

Определение: Под аⁿ понимается аⁿ =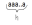.Справедливое отношение.

Определение: Элемент с тайной что для любого ae=ea называется единичным (натуральным) Единичный элемент также обозначается а^°. Единичный элемент всегда единственный. Пусть существует 2 единичных элемента e₁ и е_2.Тогда по определению единичного элемента: e₁e₂=e¹=e²=e

Определение: обратным для а называется элемент а^-1 такой, что аа^-1=a^-1a=e Справедливо соотношение (аⁿ)^-1=(a^-1)ⁿ=a^-n

38. Определение и свойства групп.

Определение: Алгебраическая структура G=<A;·> c бинарной операцией называется группой, если в G существует единичный элемент и для каждого элемента G существует обратный. Коммутативной группу принято называть абелевой группой.

также называемая абелева, — группа, в которой оператор обладает теми же четырьмя свойствами для групп плюс дополнительным — коммутативностью.

(1.Замкнутость. Если a и b — элементы G, то c = a • b — также элемент G. Это означает, что результат применения операции с любыми двумя элементами множества есть элемент этого множества.

2.Ассоциативность. Если a, b и c — элементы G, то верно (a• b) • c = a• (b •c) Другими словами, не имеет значения, в каком порядке мы применяем операцию более чем с двумя элементами.

3.Коммутативность. Для всех a и b в G мы имеем a • b = b • a. Обратите внимание, что это свойство должно быть верно только для коммутативной группы.

4.Существование нейтрального элемента. Для всех элементов в G существует элемент e, который называется нейтральным элементом, такой, что e • a = a • e = a.

5.Существование инверсии. Для каждого a в G существует элемент a', называемый инверсией, такой, что a • a' = a' • a = e.)

Пример: множество рациональных чисел относительно операций сложения образуют абелеву группу

Пример: множество невырожденных квадратных матриц одной размерности образуют группу относительно операции умножения. Единичным элементов является единичная матрица. Данная группа не является абелевой.

Определение: Группа называется мультинимативной(?????),если алгебраическая операция имеет смысл произведения. В этой группе алгебраическая операция обозначается «·», нейстральный элемент -1, а обратный элемент - a^-1 , произведение n элементов а……..а обозначается аⁿ.

Определение: группа называется аддитивной, если алгебраическая операция имеет смысл сложения. В этой группе алгебраическая операция обозначается +, нейстральный элемент -0,обратный элемент называется противоположным и обозначается –а, сумма n элементов.

Группа называется конечного порядка n, если она содержит ровно n различных элементов.

Пример: пусть х- конечное множество |х|=n, F-множество всех биентивных(???) функций f:x->x. Тогда <F;0> есть конечная группа с операцией Порядок группы равен n!

Теорема: пусть G группа 1)Обратный элемент для любого а€G является единственным. 2)Уравнение ax=b для любого a,b € G имеет единственное решение х=а^-1b.

Аналогично уравнение ха=b имеет единственное решение х=ba^-1 3)Справедливо равенство (ab)^-1=b^-1a^-1

Определение: пусть G группа подмножество H≤G называется G,если H само является группой.