
A_G_2014
.pdf
§ 7. Задачи о взаимном расположением прямых и точек на плоскости |
61 |
Рис. 16. К вычислению расстояния от точки до прямой: d > 0 (a), d < 0 (b)
§ 7. Задачи о взаимном расположением прямых и точек на плоскости
1. Определим расстояние от точки x0 = (x01, x02) до прямой l. Проще всего эта задача решается, когда прямая l задана нормальным уравнением (6.2). Действительно, поскольку |p| = 1, то (x0, p) — величина проекции вектора x0 на прямую, параллельную p, следовательно, величина δ = (x0, p) −d есть отклонение точки x0 от прямой l (см. рис. 16). Причем знак δ показывает, по какую сторону от пря-
мой l расположена точка x0. Расстояние от точки x0 до прямой l равно |(x0, p) − d|.
Пример. Найти расстояние от точки x0 = (1, −2) до прямой 3x1 − 4x2 − 26 = 0
(сделайте рисунок!). Сначала приведем прямую к нормальному виду: 35 x1−45 x2−265 = 0, т. е. p = (3/5, −4/5), d = 26/5. Теперь вычислим δ = 3/5 + 8/5 − 26/5 = −3. Расстояние от точки до прямой равно трем.
2. Даны две прямые l1 и l2, определяемые уравнениями
a11x1 + a12x2 |
= b1 |
, |
(7.1) |
|
a21x1 + a22x2 = b2. |
||||
|
||||
Требуется исследовать взаимное расположение этих прямых, т. е. выяснить, пересекаются ли эти прямые, и указать точку их пересечения.
Эта задача была нами полностью решена в 1, с. 28. Действительно, фактически, поставленная задача эквивалентна исследованию условий разрешимости системы линейных уравнений (7.1). Здесь надо различать три случая.

62 Глава 4. Введение в аналитическую геометрию
1) Определитель |
|
|
|
|
|
a11 |
a12 |
|
|
|
a21 |
a22 |
|
|
∆ = |
|
|
||
не равен нулю. Тогда система уравнений |
(7.1) |
имеет единственное ре- |
||
шение x1, x2 при любых b1, b2. Точка x = (x1, x2) — точка пересечения прямых.
2) Определитель ∆ равен нулю, но определитель
|
|
|
b1 |
a12 |
|
|
|
|
|
|
|
||
∆1 |
= |
|
b2 |
a22 |
|
, |
|
|
|
|
|
|
|
аследовательно, и определитель
∆2 = a11 b1
a21 b2
отличны от нуля. Тогда система (7.1) не имеет решений, т. е. прямые l1, l2 параллельны.
3) Все три определителя ∆, ∆1, ∆2 — нули. Это условие эквивалентно существованию числа α ≠ 0 такого, что
a21 = αa11, a22 = αa12, b2 = αb1.
Система (7.1) имеет бесконечное множество решений (фактически, уравнения системы совпадают). Прямые l1, l2 совпадают.
3. Найдем угол между прямыми y = k1x + b1 и y = k2x + b2 (см. рис. 17). Так как φ = α2 − α1, tgα1 = k1, tgα2 = k2, то
tgφ = tg(α |
|
− |
α |
) = |
tgα2 − tgα1 |
= |
k2 − k1 |
. |
|
1 + tgα2 tgα1 |
|
||||||
|
2 |
1 |
|
|
1 + k1k2 |
|||
Рис. 17. Угол между прямыми

§ 8. Различные формы уравнения плоскости |
63 |
Рис. 18. К уравнению плоскости, проходящей через точку x0, натянутой на векторы e1 и e2; а также к нормальному уравнению плоскости (x, p) − q = 0
Упражнения.
1)Найдите косинус угла между двумя прямыми, заданными уравнениями вида (6.1).
2)Найдите косинус угла между двумя прямыми, заданными уравнениями вида (6.2).
3)Используя выражение для тангенса угла между прямыми, по-
кажите, что при k1 = k2 прямые параллельны, при k1k2 = −1 ортогональны.
§ 8. Различные формы уравнения плоскости
Рассматривается трехмерное евклидово пространство. Пусть e1 и e2 — неколлинеарные векторы в трехмерном пространстве, а x0 — произвольный вектор. Уравнение
x = x0 + α1e1 + α2e2, −∞ < α1, α2 < ∞, |
(8.1) |
определяет плоскость π, проходящую через точку x0. Говорят, что эта плоскость натянута на векторы e1, e2 (см. рис. 18).
Пусть p — единичный вектор. Уравнение
(x, p) − q = 0 |
(8.2) |
определяет множество векторов, концы которых принадлежат плоскости, ортогональной вектору p и отстоящей от начала координат на расстояние q (см. рис. 18). Знак q определяет направление сдвига плоскости (по отношению к направлению вектора p). Уравнение (8.2) называют нормальным уравнением плоскости. Напомним, что нормальное уравнение прямой (6.2) имеет аналогичный вид.

64 |
Глава 4. Введение в аналитическую геометрию |
Запишем уравнение (8.1) в координатной форме (здесь и далее до конца главы используются только декартовы координаты)
x1 − x10 |
= α1e11 + α2e12, |
(8.3) |
x2 − x20 |
= α1e21 + α2e22, |
(8.4) |
x3 − x30 |
= α1e31 + α2e32. |
(8.5) |
Полагая, что x ≠ x0, рассмотрим определитель
|
|
x1 |
x10 |
e11 |
e12 |
. |
|
|
∆(x) = |
x2 |
− x20 |
e21 |
e22 |
|
|||
|
|
|
− 3 |
3 |
3 |
|
|
|
|
|
|
− x0 |
e1 |
e2 |
|
|
|
|
x3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
Равенства (8.3) – (8.5) означают, |
что если |
точка x принадлежит |
||||||
плоскости π, то столбцы этого определителя линейно зависимы, следовательно, он равен нулю. Наоборот, равенство нулю этого определителя означает, что его столбцы линейно зависимы и, поскольку векторы e1, e2 линейно независимы, то выполнены равенства (8.3)–(8.5).
Таким образом, уравнение
|
x1 |
x10 |
e11 |
e12 |
|
|
|
|
− 3 |
3 |
3 |
|
|
||
|
|
− x20 |
e21 |
e22 |
|
= 0 |
(8.6) |
x2 |
|
||||||
x3 |
− x0 |
e1 |
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
есть уравнение плоскости (в координатной форме), проходящей через точку x0 и натянутой на векторы e1, e2. Раскрывая определитель ∆(x) (например, по первому столбцу), запишем уравнение плоскости π в виде
ax1 + bx2 + cx3 + d = 0. |
(8.7) |
Здесь числа a, b, c, d очевидным образом выражаются через координаты векторов e1, e2, x0. Уравнение вида (8.7) называют общим уравнение плоскости.
Аналогично уравнению прямой уравнения (8.1), (8.2), (8.7) можно эквивалентно преобразовывать из одной формы в другую.
Упражнения.
1) Преобразовать уравнение (8.7) к нормальному виду. Ответ:
1 |
|
d |
|||
p = |
√ |
|
(a, b, c), q = −√ |
|
. |
a2 + b2 + c2 |
a2 + b2 + c2 |
||||
2) Показать, анализируя общее уравнение плоскости, что:

§ 8. Различные формы уравнения плоскости |
65 |
Рис. 19. Точки пересечения плоскости с осями координат
если a = 0, b = 0, то плоскость параллельна координатной плос-
кости x1x2;
если a = 0, то плоскость параллельна оси x1;
если d = 0, то плоскость проходит через начало координат.
3)Показать, что α = −d/a, β = −d/b, γ = −d/c — координаты
точек пересечения плоскости с осями x1, x2, x3 (см. рис. 19), проанализировать случаи, когда соответствующие знаменатели — нули.
4)Показать, что косинус угла φ между плоскостями, задаваемыми уравнениями
a1x1 + b1x2 + c1x3 + d1 = 0, a2x1 + b2x2 + c2x3 + d2 = 0,
можно вычислить по формуле
cos φ = |
|
a1a2 |
+ b1b2 |
+ c1c2 |
. |
(8.8) |
||
|
|
|
|
|
||||
√a12 + b12 + c12√a22 + b22 + c22 |
||||||||
|
|
|
||||||
5)Используя уравнение (8.6), написать уравнение плоскости, проходящей через три заданные точки. Проанализировать случай, когда эти точки лежат на одной прямой.
6)Используя нормальное уравнение плоскости (8.2), найти отклонение данной точки x0 от плоскости.
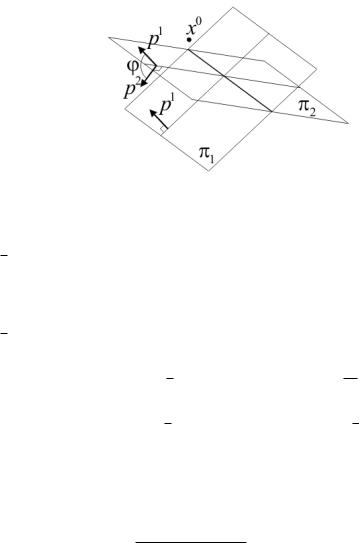
Пример. Даны плоскости π1 и π2, описываемые уравнениями |
|
2x1 − x2 + 2x3 − 3 = 0, |
(8.9) |
6x1 + 2x2 − 3x3 + 8 = 0, |
(8.10) |
и точка x0 = (1, 1, 8). Определить величину того угла между плоскостями π1, π2, которому принадлежит точка x0.
Приведем уравнения (8.9), (8.10) к нормальному виду. Имеем
√√
22 + 12 + 22 = 3, 62 + 22 + 32 = 7,
следовательно, нормальный вид уравнения (8.9) есть
(p1, x) − q1 = 0,
66 |
Глава 4. Введение в аналитическую геометрию |
Рис. 20. Плоскости π1, π2
где p1 = 13 (2, −1, 2), q1 = 1, а для уравнения (8.10) получаем
(p2, x) − q2 = 0,
где p2 = 17 (6, 2, −3), q2 = −8/7. Заметим далее, что
(p1, x0) − q1 = 13 (2 · 1 − 1 · 1 + 2 · 8 − 3) = 143 > 0,
(p2, x0) − q2 = 17 (6 · 1 + 2 · 1 − 3 · 8 + 8) = −87 < 0.
Поэтому конец вектора p1 и точка x0 лежат по одну сторону от плоскости π1, а конец вектора p2 и точка x0 лежат по разные стороны от плоскости π2 и, следовательно, точка принадлежит углу φ (см. рис. 20). Угол φ равен углу между векторами p1, p2. Используя формулу (8.8), получим
cos φ = |
2 · 6 − 1 |
· |
2 − 2 · 3 |
= |
4 |
, |
φ |
≈ |
0, 44π. |
|
3 |
· |
7 |
21 |
|||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
§ 9. Уравнения прямой в пространстве |
|
Уравнение |
(9.1) |
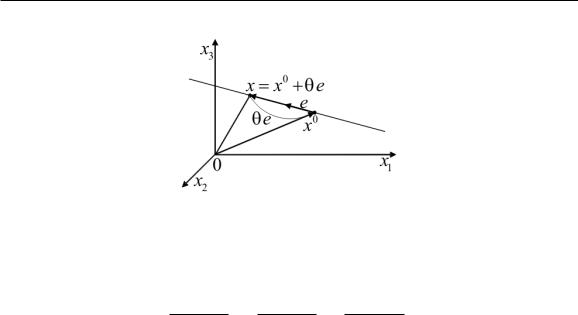
x = x0 + θe, −∞ < θ < ∞, |
определяет прямую, проходящую через точку x0 параллельно вектору e = (e1, e2, e3) (см. рис. 21).
Запишем уравнение (9.1) в координатах |
|
|
x1 − x10 |
= θe1, |
(9.2) |
x2 − x20 |
= θe2, |
(9.3) |
x3 − x30 |
= θe3. |
(9.4) |
§ 10. Задачи о взаимном расположении точек, прямых, плоскостей в пространстве 67
Рис. 21. Прямая в пространстве
Исключая из этих уравнений параметр θ, получим
x1 − x10 |
= |
x2 − x20 |
= |
x3 − x30 |
. |
(9.5) |
e1 |
|
e2 |
|
e3 |
|
|
Множество всех точек x = (x1, x2, x2), координаты которых удовлетворяют уравнениям (9.5), образуют прямую, проходящую через точку x0 параллельно вектору e. Уравнения (9.5) называют каноническими уравнениями прямой.
Упражнение. Интерпретируйте случай, когда какой-либо знаменатель в (9.5) обращается в нуль.
§ 10. Задачи о взаимном расположении точек, прямых, плоскостей в пространстве
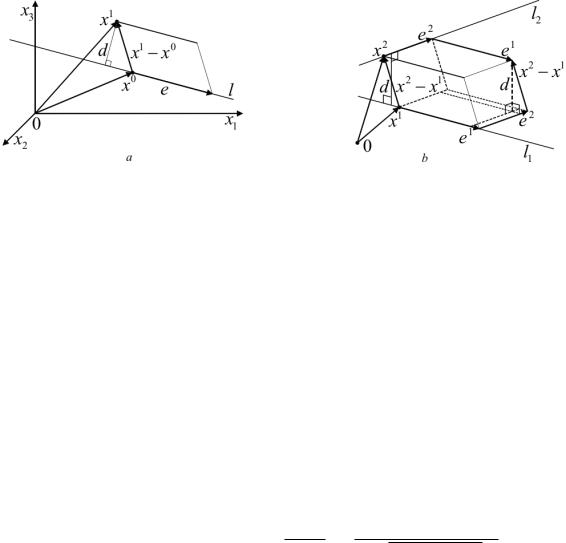
1. Найти расстояние d от прямой l, заданной уравнением (9.1),
до точки x1 = (x11, x12, x13).
Искомым расстоянием является длина перпендикуляра, опущенного из точки x1 на прямую l (см. рис. 22, a). Рассмотрим параллелограмм, построенный на векторах e и x1 − x0. Площадь этого параллелограмма равна |[e, x1 − x0]|, следовательно, d = |[e, x1 − x0]|/|e|. Для того, чтобы выразить входящие сюда величины через координаты точек x0, x1 и компоненты вектора e, нужно, в частности, воспользоваться формулой (3.3), с. 53, для компонент векторного произведения.
2. Найти расстояние d между непараллельными прямыми l1 и l2, заданными уравнениями
x = x1 + θe1, |
−∞ < θ < ∞, |
x = x2 + θe2, |
−∞ < θ < ∞. |
68 |
Глава 4. Введение в аналитическую геометрию |
Рис. 22. К вычислению расстояния от точки до прямой (a) и между прямыми (b)
Искомое расстояние, очевидно, есть длина отрезка прямой, который ортогонален l1 и l2, концы его лежат на l1 и l2 (см. рис. 22, b). Построим параллелепипед на векторах e1, e2 и x2 −x1. Понятно, что d — высота этого параллелепипеда и, следовательно, d есть отношение его
объема к площади основания.
Таким образом, d = |(e1, e2, x2 − x1)|/|[e1, e2]|. Осталось выразить все входящие в эту формулу величины через координаты точек x1, x2
икомпоненты векторов e1, e2 (см. (3.3), с. 53, и (4.1), с. 55).
3.Найти угол φ между прямой l, заданной уравнением (9.1), и плоскостью π, заданной нормальным уравнением (8.2).
Угол φ является дополнительным к углу ψ между направляющим вектором прямой e и нормальным вектором плоскости p, следователь-
но,
sin φ = cos ψ = cos(e, p) = (e, p) = e1p1 + e2p2 + e3p3 . |
|
|e| |
√e12 + e22 + e32 |
4.Определить общие точки прямой l, заданной уравнением (9.1),
иплоскости π, заданной уравнением (8.7).
Подставим значения x1, x2, x3 из (9.2) – (9.4) в уравнение (8.7). После элементарных преобразований получим
ax10 + bx20 + cx30 + d + θ(ae1 + be2 + ce3) = 0. |
(10.1) |
Возможны следующие случаи.
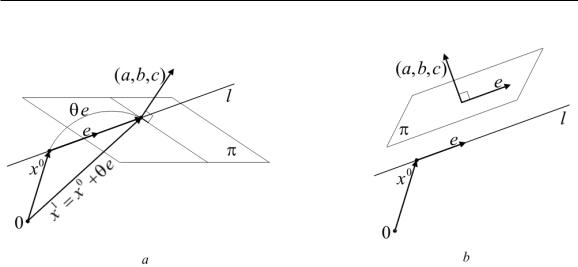
1) ae1 + be2 + ce3 ≠ 0. Это означает, что прямая l не параллельна плоскости π (почему?). Из уравнения (10.1) находим
θ = θ1 = − |
ax10 + bx20 + cx30 + d |
|
|
. |
|
ae1 + be2 + ce3 |
||
Точка x1 = x0 + θ1e — точка пересечения прямой и плоскости (см. рис. 23, a).
§ 10. Задачи о взаимном расположении точек, прямых, плоскостей в пространстве 69
Рис. 23. К определению точки пересечения прямой и плоскости (a). Прямая l, параллельная плоскости π (b)
2) ae1 + be2 + ce3 = 0, но ax01 + bx02 + cx03 + d ≠ 0. Уравнение (10.1) не имеет решений. Прямая l проходит через точку x0, не принадле-
жащую плоскости π, параллельно плоскости π (см. рис. 23, b).
3) ae1 +be2 +ce3 = 0, ax01 +bx02 +cx03 +d = 0. Любое θ (−∞, ∞) —
решение уравнения (10.1). Прямая l лежит в плоскости π.
5. Выяснить условия, при которых две прямые l1 и l2, задаваемые
уравнениями
x = x1 + θe1, θ (−∞, ∞), x = x2 + θe2, θ (−∞, ∞),
лежат в одной плоскости.
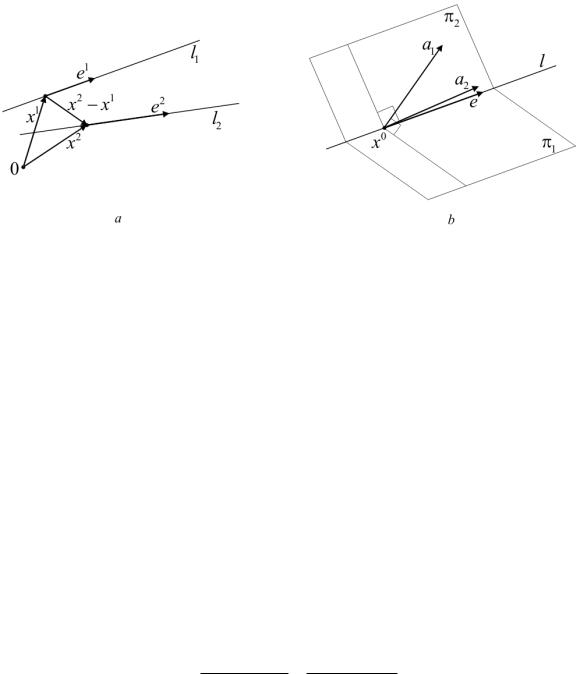
Если прямые l1 и l2 лежат в одной плоскости, то векторы x2− x1, e1, e2 лежат в одной плоскости (см. рис. 24, a), иначе говоря, компланарны. Обратно, если векторы x2 − x1, e1, e2 компланарны, то прямые l1, l2 лежат в одной плоскости. Используя результаты § 4, непосредственно получаем, что для принадлежности прямых l1, l2 одной и той же плоскости необходимо и достаточно, чтобы смешанное произведение (x2 − x1, e1, e2) равнялось нулю.
6. Написать уравнение прямой l, являющейся пересечением двух различных и не параллельных плоскостей π1, π2, задаваемых уравнениями
a1x1 + b1x2 + c1x3 + d1 = 0, a2x1 + b2x2 + c2x3 + d2 = 0. (10.2)
Найдем сначала какую-либо точку, принадлежащую обеим плоскостям (см. рис. 24, b). Иными словами, найдем какое-то реше-
70 |
Глава 4. Введение в аналитическую геометрию |
Рис. 24. К компланарности прямых l1 и l2 (a). К построению уравнения прямой, по которой пересекаются две плоскости (b)
ние x1, x2, x3 системы уравнений (10.2). По условию плоскости не параллельны, следовательно, векторы
a1 = (a1, b1, c1) и a2 = (a2, b2, c2),
нормальные к ним, не коллинеарны. Значит не выполняется хотя бы одно из равенств
a1 |
= |
b1 |
= |
c1 |
. |
|
a2 |
b2 |
c2 |
||||
|
|
|
Примем для определенности, что a1b2 − a2b1 ≠ 0. Положим x3 = 0, тогда из (10.2) получаем
a1x1 + b1x2 = −d1, a2x1 + b2x2 = −d2.
Решая эту систему, приходим к выводу, что точка
|
= ( |
b1d2 |
b2d1 |
|
a2d1 |
a1d2 |
, 0) |
x0 |
a1b2 |
− |
, |
a1b2 |
− |
||
a2b1 |
a2b1 |
||||||
|
|
|
− |
|
|
− |
|
принадлежит прямой l, по которой пересекаются плоскости π1, π2. Найдем теперь направляющий вектор e этой прямой. Вектор e ор-
тогонален каждому из векторов a1 и a2, следовательно, можно взять
вектор e, равным их векторному произведению: |
|
|||||
|
|
i1 |
i2 |
i3 |
|
|
e = [a1, a2] = |
|
a1 |
b1 |
c1 |
|
(10.3) |
|
. |
|||||
|
|
|
|
|
|
|
|
|
a2 |
b2 |
c2 |
|
|
|
|
|
|
|||
