
Tensor-Gotman
.pdf
Теорема 5.14 Если Ti1i2 ...in (r) - тензорное поле n -го ранга, то величина производной тензора ∂ ∂xi Ti1i2...in есть тензорное поле n +1-го ранга.
∂xi Ti1i2...in есть тензорное поле n +1-го ранга.
Д о к а з а т е л ь с т в о. Заметим, что при переходе из системы координат xi к xi' справедливо равенство
|
∂ |
|
' |
|
∂ |
|
|
|
|
Ti1i2 |
|
= |
|
T 'i1i2 ...in . |
(54.14) |
|
|
||||||
|
∂xi |
...in |
∂x'i |
||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При повороте xi' |
= ∑αi j xi (i =1,2,3) . Отсюда в силу условия ( - «для любого») |
||||||||||||||||||||||
|
|
j =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
1, |
j = k |
|
|||||
|
|
∑αi jαik |
|
= ∑α jiαki = δ jk |
= |
(55.14) |
|||||||||||||||||
|
|
|
|
j ≠ k |
|||||||||||||||||||
|
|
i =1 |
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
0, |
|
||||||
следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
||
|
|
|
x j |
= ∑αi j x'i |
или |
j |
=αi j . |
(56.14) |
|||||||||||||||
|
|
|
' |
||||||||||||||||||||
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
∂xi |
|
|
|
|
|
|
|||
Поэтому оператор производной по x' |
имеет вид |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
3 |
∂x j |
|
|
∂ |
|
|
n |
|
|
|
|
∂ |
|
|
|||||
|
|
|
|
= ∑ |
|
|
|
= ∑αi j |
. |
(57.14) |
|||||||||||||
|
|
|
∂x' |
|
∂x' |
|
∂x j |
∂x j |
|||||||||||||||
|
|
|
i |
|
j =1 |
i |
|
|
|
|
|
|
|
j =1 |
|
|
|
|
|
|
|||
Замечание 15.14 В равенстве (56.14) |
|
|
предполагается, что все x'j ( j ≠ i) |
и xi (i ≠ j) |
|||||||||||||||||||
фиксированы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь видно, что величина ∂ ∂xi |
Ti i |
2 |
...i |
n |
преобразуется как тензор n +1-го ранга, а |
||||||||||||||||||
именно |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∂ |
T 'i1i2 ...in = |
|
∑αi j αi1 j1 ...αin jn |
|
∂ |
T ' j1 j2 ... jn , |
(58.14) |
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
∂x' |
|
|
∂xi |
|||||||||||||||||||
|
i |
|
j, |
j1, j2 ,..., jn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а число компонент такого тензора равно 3n+1 . Тем самым данная теорема доказана. Определение 21.14 Тензорное поле, зависящее от времени Tik = Tik (r,t) , называется
нестационарным.
Примеры: Характеристиками нестационарных тензорных полей являются функции точки и времени
ϕ =ϕ (r,t) , a = a (r,t) , pik = pik (r,t) и т.п.
Замечание 16.14 Чаще всего рассматриваются непрерывные тензорные поля. Замечание 17.14. Все формулы тензорной алгебры справедливы при изучении тензорных полей.
Определение 22.14 Если каждому допустимому численному значению скалярной
величины t соответствует одно вполне определённое значение тензорной величины Tik ,
то говорят, что задана тензор – функция от скалярного аргумента
Tik = Tik (t) |
(59.14) |
Замечание 18.14 Если напряжённое состояние меняется с течением времени, то в каждой точке надо рассматривать девять функций времени pik = pik (t) , которые для каждого
значения t образуют тензор.
81
Определение 23.14 Производной по t от тензора с компонентами pik = pik (t)
называется тензор, компоненты которого (в постоянной по времени системе координат) вычисляются как пределы
d pik |
= lim |
pik (t + |
t) − pik (t) |
(60.14) |
dt |
|
t |
||
t→0 |
|
|||
Замечание 19.14 Производные тензоров более высокого порядка получаются по тем же правилам, что и для векторов.
Замечание 2014 Дифференцирование тензора по скалярному аргументу не меняет его ранга.
Дифференцирование тензорных полей
В ортогональной декартовой системе координат, где радиус – вектор любой точки имеет вид
x = xiei , |
(61.14) |
поля тензоров различного ранга можно записать в индексных и символических
обозначениях, например, |
|
|
|
а) скалярное поле |
|
|
|
ϕ =ϕ(xi ,t) или ϕ =ϕ(x,t) |
(62.14) |
||
б) векторное поле |
=υi (xi ,t) или v = v(x,t) |
|
|
υi |
(63.14) |
||
в) поле тензора второго ранга |
j = Ti j (x,t) или T = T(x,t) |
|
|
Ti |
(64.14) |
||
Обозначение 1.14 Дифференцирование компонент тензора по координате xi |
обозначается |
||
дифференциальным оператором |
∂ ∂xi |
(65.14) |
|
или сокращённо в индексной записи |
|||
∂i , |
(66.14) |
||
|
|||
что указывает на то, что это дифференциальный оператор первого ранга.
Обозначение 2. В символических обозначениях для записи векторной операции употребляется общеизвестный символ (набла), который расшифровывается так:
|
|
|
|
|
|
= ei |
|
∂ |
= ei ∂i |
|
|
|
|
|
|
|
|
(67.14) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
∂xi |
|
|
|
|
|
|
|
|
|
||||
Обозначение 3. Частное дифференцирование по переменной |
xi |
иногда |
изображают |
|||||||||||||||||||
нижним индексом после запятой, как показано в следующих примерах: |
|
|||||||||||||||||||||
а) |
∂ϕ |
=ϕ,i , |
б) |
∂υi |
|
=υi ,i , |
в) |
∂υi |
=υi , j , |
|
|
|
(68.14) |
|||||||||
|
|
|
|
|||||||||||||||||||
|
|
∂xi |
|
|
|
|
∂xi |
|
|
|
|
|
|
∂x j |
|
|
|
|
|
|
||
|
|
∂2υ |
i |
|
|
|
|
|
|
∂T |
|
|
|
|
∂2T |
|
|
|||||
г) |
|
|
|
=υ |
, |
j k |
д) |
|
|
i j |
= T |
, |
k |
, |
е) |
|
i j |
= T |
(69.14) |
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
i j |
|
|
|
∂xk ∂xm |
i j,k m |
|
||||
|
|
∂x j ∂xk |
|
|
|
|
|
∂xk |
|
|
|
|
|
|
||||||||
Замечание 21.14 Эти примеры показывают, что при дифференцировании оператор ∂i
приводит к тензору на один порядок выше исходного, если i остаётся свободным индексом (случаи «а» и «в»), и к тензору на один порядок ниже исходного, если индекс i становится индексом суммирования ( случай «б»).
Замечание 22.14 Для справки ниже приведены важные дифференциальные операторы, часто употребляемые в механике сплошной среды,
82
gradϕ = ϕ = |
∂ϕ |
ei |
или |
∂iϕ =ϕ,i , |
(70.14) |
|
|||||
div v = v, |
∂ xi |
или |
∂iυi =υi,i , |
(71.14) |
|
|
|
||||
rot v = × v, |
|
|
или |
εi jk ∂ jυk = εi jkυk, j , |
(72.14) |
2ϕ = ϕ, |
|
|
или |
∂iiϕ = ϕ,ii . |
(73.14) |
Задача 1.14 Пользуясь индексными обозначениями, доказать векторные тождества:
а) × ϕ = 0 , б) ×a = 0 .
а) Согласно (67.14), ϕ записывается в виде eiϕ ,i и тогда v = × ϕ имеет компоненты
υi = εi jk ∂ jϕ,k = εi jkϕ, k j .
Но εijk . антисимметричен по индексам j и k , тогда как ϕ,k j .симметричен по этим индексам. Следовательно, произведение εijkϕ,kj . обращается в нуль. К тому же
результату можно прийти, вычислив отдельно каждую компоненту v , например
υ1 = ε123ϕ,23 +ε132ϕ,32 = (ϕ,23 −ϕ,32 ) = 0.
б) ×a = λ = (εijk ak, j ),i = εijk ak, ji = 0 , так как ak,ij = ak, ji и εijk = −ε jik .
Задача 2.14 Пользуясь индексными обозначениями, доказать векторное тождество
×(a ×b) = (b )a −b ( a) +a ( b) −(a )b
Доказательство. ×(a ×b) = v можно написать в виде υp = ε p q iεi jk ∂qa jbk и тогда на основании формулы примера 8 главы 1 ε pqsεsqr = δqpδrq −δqqδrp получается
υp = ε p q iεi jk (a jbk ),q = ε p q iεi jk (a j,qbk + a jbk,q ) =
= (δ p jδq k −δ p kδq j ) (a j,qbk + a jbk,q ) = a p,qbq − aq,qbp + a pbq,q − aqbp,q .
Аэто значит, что
v= (b )a −b ( a) +a ( b) −(a )b
Поле тензора 2-го ранга. Поток тензорного поля
Рассмотрим поле тензора 2-го ранга T (r) , имеющего компоненты Tik = Tik (r) .
Примерами полей тензора 2-го ранга могут служить поле тензора напряжений в упругой среде и поле моментов инерций в твёрдом теле.
Рассмотрим двустороннюю кусочно-гладкую поверхность S , помещённую в тензорное поле T (r) . Для каждого элемента dS этой поверхности определим
положительный орт нормали n .
Определение 24.14. Потоком тензорного поля через поверхность называется
поверхностный интеграл, взятый от скалярного произведения тензора Т на вектор нормали: n
W = ∫∫T n dS |
(74.14) |
S |
|
Замечание 23.14 Поток тензорного поля является вектором, в отличие от потока векторного поля
Π = ∫∫∫divF dV = ∫∫F n dσ |
(75.14) |
|
V |
Σ |
|
Компоненты потока тензорного поля равны
83
Wi = ∫∫Tik nk dS = ∫∫(Ti1 n1 +Ti2 n2 +Ti3 n3 )dS |
(76.14) |
|
S |
S |
|
Если свёртывание происходит по вторым индексам, то |
|
|
|
Wi = ∫∫Tki nk dS |
(77.14) |
|
S |
|
Несколько приложений потока поля тензора 2-го ранга.
Приложение 1. Пусть Tik ≡ pik - тензор напряжений в упругом теле. Выделим в этом
теле некоторую поверхность и определим равнодействующую Р всех сил напряжения, приложенных к этой поверхности (замкнутой или незамкнутой) . Если pn - напряжение у
элемента dS с нормалью n , то равнодействующая |
|
|
P = ∫∫pn dS |
(78.14) |
|
и её компоненты |
S |
|
= ∫∫pnk dS , |
|
|
Pk |
(79.14) |
|
|
S |
|
где pnk = pik ni . |
|
|
Следовательно, |
= ∫∫pik ni dS |
|
Pk |
(80.14) |
|
|
S |
|
Итак, поток тензора напряжений через поверхность, взятую в упругой среде, равен равнодействующей всех сил напряжений, приложенных к этой поверхности. Приложение 2. Вычисление потока единичного тензора δik через замкнутую поверхность
|
|
W = ∫∫δikn dS |
|
(81.14) |
|||
|
|
S |
|
|
|
|
|
В тензорных обозначениях получается |
|
|
|
|
|
||
|
|
Wi = ∫∫δki nk |
dS = ∫∫ni |
dS , |
(82.14) |
||
|
|
S |
|
S |
|
|
|
Поскольку |
∫∫n dS = 0 |
(это следует из того, |
что поток через замкнутую поверхность, |
||||
|
S |
|
|
|
|
есть div F = 0 , равен |
|
внутри которой нет |
ни источников, |
ни |
стоков, то |
нулю |
|||
Π = ∫∫∫0 dV = ∫∫const n dS = const∫∫n dS =0 ), то |
поток |
единичного тензора |
через |
||||
V |
S |
Σ |
|
|
|
|
|
замкнутую поверхность равен нулю.
Дивергенция тензорного поля.
Дивергенция тензора 2-го ранга, как и поток этого поля, является вектором и
определяется следующим пределом |
|
||
divT = Vlim→0 |
1 |
∫∫T n dS |
(83.14) |
V |
|||
|
|
S |
|
Здесь поверхность S , ограничивающая объём V , стягивается к рассматриваемой точке так, что её площадь вместе с величиной объёма V стремится к нулю. Предел не зависит от формы замкнутой поверхности S .
84

Компоненты вектора divT получается путём дифференцирования компонент тензора Tik по координатам и свёртывания по тем индексам, по которым производится свёртывание справа в (77.14). Таким образом,
|
∂Tik |
1 |
|
|
|
|
|||
(divT )i = |
∂ x |
|
= Vlim→0 |
|
|
|
∫∫Tik nk dS, |
|
|
k |
V |
|
|||||||
|
|
|
|
|
|
S |
|
(84.14) |
|
|
∂Tki |
1 |
|
|
|
||||
(divT )i = |
|
∫∫Tk i nk dS |
|
|
|||||
|
= Vlim→0 |
|
|
|
|
||||
∂ xk |
V |
|
|
||||||
|
|
|
|
|
|
|
S |
|
|
Если использовать оператор Гамильтона, то выражение дивергенции тензора запишется в виде
|
|
divT = T |
(85.14) |
Производная тензорного поля по направлению.. |
|
||
|
Отыскивая производную тензорного поля по какому-нибудь направлению, |
||
определяемому вектором l , а также применяя |
формулу (12.14) к вектору А |
||
( |
∂A |
= l A = (l )A ), получают при определении производной тензора по направлению |
|
|
|||
|
∂l |
|
|
∂∂Tl = l T .
Компоненты этого тензора в прямоугольной декартовой системе координат в символической записи с учётом формулы
|
|
|
|
|
∂ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
T = im |
|
|
|
|
T |
|
|
|
имеют вид |
|
|
∂xm |
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
∂Tik |
= (l im ) |
∂Tik |
= lm |
∂Tik |
|
||||
|
∂l |
|
|
∂xm |
||||||
|
|
∂xm |
|
|||||||
Бесконечная совокупность производных |
|
∂T |
|
тензора 2-го ранга по направлению |
||||||
|
∂ l |
|||||||||
|
|
|
|
|
|
|
|
|||
определяется компонентами тензора 3 –го ранга ∂Tik .
∂xm
Замечание 24.14 Операция образования ротора векторного поля неприменима к тензорным полям 2-го ранга.
Теорема Остроградского – Гаусса в тензорном поле
Эта теорема связывает поверхностный интеграл от некоторого гладкого1
тензорного поля n -го ранга |
с объёмным интегралом от тензорного поля |
(n +1) - го |
|||||||
ранга. |
|
|
|
|
|
(x1, x2 , x3 ) . Тогда имеет |
|||
Т е о р е м а 1.14. Пусть дано |
|
гладкое тензорное поле |
Tl l |
...l |
n |
||||
место равенство |
|
|
1 2 |
|
|
|
|||
|
|
|
|
|
|
|
|||
3 |
∂ |
3 |
|
|
|
|
|
||
∑∫∫∫ |
Ti1i2 ...in dV = ∫∫∑Ti1i2 ...in dSi1 , |
(86.14) |
|||||||
∂ xl |
|||||||||
i1 =1 V |
1 |
S i1 =1 |
|
|
|
|
|
||
1 Гладким полем называется тензорное поле, каждая компонента которого обладает непрерывными частными производными по всем аргументам
85

где d V - элемент объёма, dS(dS1 , dS2 , dS3 ) - вектор, направленный вдоль внешней
нормали к поверхности, причём длина вектора dS численно равна площади элемента поверхности S .
Д о к а з а т е л ь с т в о. Рассмотрим произвольный объём V , ограниченный поверхностью
S . Разобьем |
этот |
объём на |
|
|
элементарные |
объёмы, |
|
которые с заданной степенью |
||||||||||||||||||||||||
точности аппрксимируются кубами. Докажем формулу (86.14) |
|
для элементарного куба с |
||||||||||||||||||||||||||||||
рёбрами, параллельными |
|
координатным осям. Интеграл, стоящий в |
левой части |
|||||||||||||||||||||||||||||
равенства (86.14), для куба может быть преобразован следующим образом: |
|
|||||||||||||||||||||||||||||||
|
∫∫∫ |
|
|
∂ |
|
T1 i2i3...in dx1dx2dx3 + ∫∫∫ |
∂ |
|
T2 i2i3...in dx1dx2dx3 + |
|
||||||||||||||||||||||
∂ x |
|
∂ x |
2 |
|
||||||||||||||||||||||||||||
|
|
V |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
+ ∫∫∫ |
|
∂ |
T3 i |
2i3...in dx1dx2dx3 = ∫∫T1 i2i3...in |
|
x1 +dx1 |
dx2dx3 + |
(87.14) |
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
∂ x3 |
|
x |
|
||||||||||||||||||||||||||||
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
+ ∫∫T2 i2i3...in |
|
|
x2 +dx2 |
dx1dx3 + ∫∫T3 i2i3...in |
|
|
x3 +dx3 |
dx1dx2. |
|
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
x2 |
|
|
|
|
|
x3 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|||
Из рис.13.14 ясно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
C dS1 (0, dx2 , dx3 ) |
|
|
|
|
|
G |
|
|
|
||||||||||||||
|
|
B |
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
A |
|
|
|
|
|
|
|
dS2 (−dx1,0, dx3 ) |
|
E |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Рис. 13.14 |
|
|
К теореме Остроградского - Гаусса |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫∫T1i2i3 |
...in |
|
x1 |
+dx1 |
dx2dx3 |
= |
∫∫T1i2i3...in dx2dx3 − |
|
∫∫T1i2i3...in dx2dx3 |
(88.14) |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|||||||||||||||||||||||||||
S |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
ABCD |
|
|
|
|
EFGH |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Так как dS1 = 0 для всех граней, за исключением ABCD и EFGH , то |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
∫∫T1i2 |
...in |
|
x1 +dx1 |
dx2dx3 = |
∫∫T1i2 ...in dS1 . |
|
|
(89.14) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
1 |
|
|
|
S1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аналогично получаем |
|
|
|
|
|
|
|
|
|
x2 |
+dx2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
∫∫T2 i2 ...in |
|
|
dx1dx3 |
= ∫∫T2 i2 ...in dS2 |
|
|
(90.14) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
x3 |
+dx3 |
|
|
S2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
∫∫T3i2 ...in |
|
|
dx1dx2 |
= ∫∫T3i2 ...in dS3 |
|
|
(91.14) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
S3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
S3 |
|
|
|
|
|
||||
Подставляя (89.14), (90.14) и (91.14) в (87.14), получим (86.14). Итак, теорема справедлива для любого элементарного объёма V , так как сумма интегралов по поверхности всех кубов даёт интеграл по поверхности, ограничивающей объём V , ибо интегралы по внутренним сторонам кубов взаимно уничтожаются за счёт различного направления нормалей на смежных сторонах.
Для n =1 величины Tl - это компоненты вектора. Равенство (86.14) переписывается в виде
86

∫∫∫ F dV = ∫∫∫divF dV = ∫∫F n dS = ∫∫Fn dS |
(92.14) |
|||
V |
V |
SV |
SV |
|
т.е. поток вектора через замкнутую поверхность равен объёмному интегралу от дивергенции вектора.
Можно сказать, как уже указывалось выше, что величина divF |
характеризует |
||||||||||||||||||||||||||
плотность источников (и стоков) данного векторного поля. |
|
||||||||||||||||||||||||||
Для n = 2.имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||
∑∫∫∫ |
Ti |
j dτ = ∫∫∑Ti j dSi |
(93.14) |
||||||||||||||||||||||||
∂ xi |
|||||||||||||||||||||||||||
|
i=1 |
|
V |
|
i |
|
|
|
|
|
|
|
|
S |
|
i1=1 |
|
|
|
|
|||||||
Рассмотрим тензор |
|
|
|
|
Si j i |
|
|
|
|
|
|
≡ δi |
jTi i |
|
|
|
|
(94.14) |
|||||||||
|
|
|
|
|
|
i |
...i |
n |
|
...i |
n |
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|||||||
Покажем, что в этом случае из теоремы Остроградского – Гаусса следует равенство |
|||||||||||||||||||||||||||
∫∫∫∂ xi |
|
|
|
|
|
|
|
|
|
∫∫ |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
∂ |
Tj |
j |
|
... |
j |
|
dτ = |
|
|
|
Tj |
j |
... j |
|
dSi |
(95.14) |
||||||
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|||||||||||||||
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|||||
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
Непосредственным следствием формулы (80.14) |
|
является соотношение |
|
||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∑Si j i1i2 ...in dSi |
≡ Ti1i2 ...in dS j |
|
(96.14) |
||||||||||||||||||||||||
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Продифференцировав и просуммировав (94.14), найдём, что |
|
||||||||||||||||||||||||||
3 |
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|||||
∑ |
|
|
Si j i1i2 ...in |
≡ |
|
|
Ti1i2 ...in |
(97.14) |
|||||||||||||||||||
∂xi |
∂x j |
||||||||||||||||||||||||||
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Применим теорему 1.14 к левой части (97.14), тогда получим |
|
||||||||||||||||||||||||||
3 |
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||
∫∫∫∑ |
|
Si |
j i1i2 ...in dV = ∑∫∫Si |
j i1i2 ...in dSi |
(98.14) |
||||||||||||||||||||||
∂ xl |
|
||||||||||||||||||||||||||
V i =1 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
i =1 S |
|
|
|
|
|
||||||||
а из (97.14) и (98.14) следует, что |
|
|
|
|
∫∫∫∂ x j |
|
|
|
|
|
|||||||||||||||||
∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
T i2i3 |
...in dSi |
|
= |
|
|
|
∂ |
|
T i2i3..in d V . |
(99.14) |
|||||||||||||||
|
S |
|
V |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Теперь формула (95.14) становится очевидной и даёт тензорную запись теоремы
Остроградского - Гаусса.
§ 15 Основные определения и выводы коэффициентов Ламэ
e 3
ξ2 |
= const |
ξ1 |
= const |
|
M |
|
e2 |
O |
e1 ξ3 = const |
||
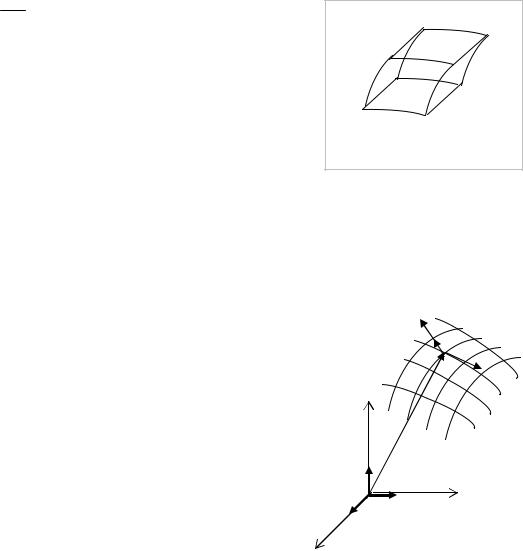
Рис. 1.15 Координатные поверхности
При решении задач механики сплошной среды для перехода из одной системы координат в другую удобно иметь общий метод, который бы давал простые формулы такого перехода. Такие формулы получаются с
помощью коэффициентов Ламэ.
Для выводы коэффициентов Ламэ рассмотрим в пространстве произвольную точку М.
Положение точки М удобно задать радиусом – вектором
r = x1e1 + x2e2 + x3e3 , |
(1.15) |
но во многих задачах выгоднее переходить к более удобным криволинейным координатам ξ1 ,ξ2 ,ξ3 ,
которые выражаются так (рис. 1.15):
87

ξ1 (r) =ξ1 (x1 , x2 , x3 ), ξ2 (r) =ξ2 (x1 , x2 , x3 ), ξ3 (r) =ξ3 (x1 , x2 , x3 ). |
(2.15) |
И обратно можно выразить радиус – вектор как r = r (ξ1 ,ξ2 ,ξ3 ), а, следовательно, можно
выразить x1 , x2 , x3 через ξ1 ,ξ2 ,ξ3 |
|
|
x1 = x1 (ξ1 ,ξ2 ,ξ3 ), x2 |
= x2 (ξ1 ,ξ2 ,ξ3 ), x3 = x3 (ξ1 ,ξ2 ,ξ3 ). |
(3.15) |
Пусть заданы поверхности равного уровня |
|
|
ξ1(r) = const, |
ξ2 (r) =const, ξ3 (r) = const. |
(4.15) |
Каждое равенство образует некоторое семейство поверхностей. Через произвольную точку М проходит по одной поверхности какого-нибудь одного семейства. Эти поверхности называются координатными. Линии пересечения называются
координатными линиями.
Замечание 1.15 На координатной линии ξ1 меняется только координата ξ1 , а остальные координаты ξ2 ,ξ3 остаются постоянными.
Введём в рассмотрение единичные векторы e1 ,e2 ,e3 , направленные по касательным к
координатным линиям в точке М в сторону возрастания, соответственно, переменных
ξ1 ,ξ2 ,ξ3 .
Рассмотрим радиус–вектор |
r = r (ξ1 ,ξ2 ,ξ3 ) и составим производную |
∂r |
. |
Поскольку |
|||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ξ1 |
вектора r |
|
при дифференцировании ξ2 и |
ξ3 |
|
|
|
считаются |
постоянными, годографом |
|||||||||||||||||||||||||||||||||||||||||
является координатная линия ξ1 , а потому вектор |
|
|
∂r |
|
имеет направление касательной |
||||||||||||||||||||||||||||||||||||||||||
|
|
∂ξ1 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
к координатной линии ξ1 , то есть |
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= H e , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.15) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ξ1 |
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где H |
1 |
- длина |
вектора |
. |
В |
|
силу |
того, |
|
что |
|
|
e |
|
единичный |
вектор, справедливо |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
∂ξ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
∂r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
H1 |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.15) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ξ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
или, так как |
|
|
|
|
|
∂r |
|
|
∂x1 |
|
|
|
|
|
|
|
∂x2 |
|
|
|
|
|
∂x3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
= |
|
e |
+ |
|
e |
|
+ |
|
e , |
|
|
|
|
|
|
|
|
(7.15) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
∂ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂ |
ξ |
|
|
1 |
|
|
|
∂ξ |
|
1 |
|
|
|
∂ξ |
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||
то |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
= (∂ x |
|
|
|
)2 |
|
+ (∂ x |
|
|
|
|
|
)2 |
|
|
|
(∂ x |
|
|
|
|
|
)2 . |
|
|
|
|
||||||||||||||||
|
|
|
|
H 2 |
∂ξ |
1 |
|
2 |
∂ξ |
1 |
+ |
3 |
∂ξ |
|
|
|
|
(8.15) |
|||||||||||||||||||||||||||||
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||
Аналогичные рассуждения приводят к совокупность формул |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂r |
= H e |
, |
|
|
∂r |
|
= H |
|
e |
|
, |
|
|
∂r |
|
|
= H |
|
e |
|
. |
|
|
|
|
(9.15) |
|||||||||||||||||
|
|
|
|
∂ξ |
|
|
∂ξ |
|
|
|
|
|
|
|
∂ξ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
1 |
1 1 |
|
|
2 |
|
|
|
|
|
|
2 |
|
2 |
|
|
|
3 |
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
= (∂ x |
|
|
|
)2 |
|
+ (∂ x |
|
|
|
|
|
)2 + (∂ x |
|
|
|
|
|
)2 . |
|
|
|
|
||||||||||||||||||||
|
|
|
|
H 2 |
∂ξ |
i |
|
2 |
∂ξ |
i |
3 |
∂ξ |
i |
|
|
|
(10.15) |
||||||||||||||||||||||||||||||
|
|
|
|
i |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Определение 1.15 Значения H1 , H 2 , H3 |
называются коэффициентами Ламэ. |
|
|||||||||||||||||||||||||||||||||||||||||||||
Рассмотрим |
три |
вектора |
gradξ i , |
то |
есть |
|
gradξ1, |
|
gradξ2 , |
gradξ3. |
Каждый из |
||||||||||||||||||||||||||||||||||||
векторов gradξ i |
направлен по нормали |
|
|
к координатной поверхности |
ξ i = const . Если |
||||||||||||||||||||||||||||||||||||||||||
ввести обозначение |
вектора |
нормали |
к |
|
поверхности |
|
в |
виде |
e *i |
в направлении |
|||||||||||||||||||||||||||||||||||||
возрастающих значений ξ i (от одной координатной поверхности к другой), то получим
88

|
|
|
|
|
|
gradξi |
|
= hie *i , |
(i =1,2,3) |
|
|
(11.15) |
||||||
где hi длина вектора gradξi . Очевидно, что |
|
|
|
|
|
|
|
|
|
|
||||||||
h2 |
= (gradξ |
i |
)2 |
= (∂ξ |
i |
∂ x )2 + (∂ξ |
i |
∂ x |
2 |
)2 |
+ (∂ξ |
i |
∂ x |
3 |
)2 |
(i =1,2,3) |
(12.15) |
|
i |
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
Величины h1 , h2 , h3 являются дифференциальными параметрами первого порядка. Коэффициенты Ламэ определяются по формулам
Hi = (∂ x1 ∂ξi )2 + (∂ x2 ∂ξi )2 + (∂ x3 ∂ξi )2 |
(13.15) |
Замечание 2.15 Обычно используются ортогональные криволинейные координаты.
Смысл коэффициентов Ламэ
Следует вспомнить из курса дифференциальной геометрии, что приращение радиуса – вектора связано с приращением дифференциала длины дуги пространственной кривой, а модуль дифференциала радиуса – вектора равен дифференциалу длины дуги
но с другой стороны |
|
|
|
|
|
|
|
|
d r |
|
= d s , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(14.15). |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
d r = |
|
∂r |
dξ |
|
+ |
∂r |
dξ |
2 |
+ |
|
∂r |
|
dξ |
3 |
= H dξ e |
+ H |
2 |
dξ |
2 |
e |
2 |
+ +H |
3 |
dξ |
3 |
e |
3 |
, |
(15.15) |
||||||
|
∂ξ |
|
|
|
∂ξ |
|
|
||||||||||||||||||||||||||||
|
|
1 |
|
∂ξ |
2 |
|
|
|
3 |
|
|
|
|
1 1 1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
d r = |
|
∂si |
dξk ei |
= Hidξiei |
|
|
|
|
|
|
|
|
|
|
|
|
(16.15) |
||||||||||
|
|
|
|
|
|
|
|
∂ξk |
|
|
|
|
|
что (dr)2 = (d s)2 , |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Возводя в |
квадрат |
|
обе части |
равенства (16.15) и замечая, |
|
ei |
2 =1, |
||||||||||||||||||||||||||||
ei ek = 0 (i ≠ k) , получим для квадрата длины элемента d r формулу |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
(d r)2 |
= H12 (dξ1 )2 + H 22 (dξ2 )2 + H32 (dξ3 )2 . |
|
|
|
|
|
|
|
|
|
|
|
|
(17.15) |
|||||||||||||||||||
и, следовательно, квадрат длины дуги тоже выражается через коэффициенты Ламэ |
|
||||||||||||||||||||||||||||||||||
|
|
(d s)2 |
= H12 (dξ1 )2 + H 22 (dξ2 )2 + H32 (dξ3 )2 . |
|
|
|
|
|
|
|
|
|
|
|
|
(18.15) |
|||||||||||||||||||
Отсюда для ортогональных криволинейных координат выражение |
для составляющих |
||||||||||||||||||||||||||||||||||
вектора dr имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
то есть, |
|
|
|
|
|
|
|
d si |
= Hidξi . |
|
(i =1,2,3) |
|
|
|
|
|
|
|
|
|
|
|
(19.15) |
||||||||||||
|
|
|
|
ds1 = H1dξ1, ds2 = H 2dξ2 , |
ds3 = H3dξ3 |
|
|
|
|
|
|
(20.15) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Через коэффициенты Ламэ в ортогональных криволинейных координатах ξi выражаются элементы длины дуги s1 , s2 , s3
d s = H12 (dξ1 )2 + H 22 (dξ2 )2 + H32 (dξ3 )2 . |
(21.15) |
Замечание 3.15 Таким образом, коэффициентов Ламэ дают связь дифференциала длины дуги на координатной поверхности с координатными линиями ξi
d sk |
= H k , |
d ξk |
= |
1 |
|
|
H k |
||
dξk |
dsk |
|||
Установим связь между коэффициентами Ламе и величинами
введенными в (11.15) и (12.15) координаты градиента gradξk в виде
gradξ |
k |
= |
∂ξk |
e |
i |
= h e |
+ h e |
|
+ h e |
|
|
|
|
||||||||
|
|
∂si |
1 1 |
2 |
2 |
3 |
3 |
|||
(22.15)
h1, h2 , h3 ,
(23.15)
Для криволинейных координат выражение дифференциала радиуса - вектора имеет вид (15.15), так что составляющими вектора d r являются
89
|
d sk |
= Hk |
или d sk |
= H k dξk . |
||
|
dξk |
|||||
|
|
|
|
|
|
|
С другой стороны, |
|
|
dξk |
|
|
|
|
|
|
|
|
= h |
|
|
|
|
|
|
||
|
|
|
|
d sk |
k |
|
|
|
|
|
|
||
Отсюда получается
hi =1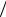 Hi
Hi
Вывод дифференциалов длины дуги, площади и объёма
Пусть d r = MN , где N - бесконечно близкая к M точка.
Проведем через N три координатных поверхности, которые вместе с тремя координатными поверхностями, проходящими через точку M , образуют криволинейный бесконечно малый параллелепипед. Рёбрами этого параллелепипеда будут дифференциалы длины дуги
(20.15)
ds1 = H1dξ1, |
ds2 = H 2dξ2 , ds3 = H3dξ3 , |
но тогда грани |
его будут иметь площади, равные |
(24.15)
(25.15)
(26.15)
M 3 N1 N2 N
M
M 2
M1 N3
Рис. 2.15 Элемент объёма
дифференциалу площади
dσ1 = H 2 H3d ξ2 d ξ3 , |
dσ2 = H3 H1d ξ3d ξ1 , |
|
dσ3 = H1H 2 d ξ1d ξ2 |
|
|
|
|
|
|
|
(27.15) |
|||||||||||||||||||||||||||||||||||
а дифференциал объёма (рис. 2.15) получается в виде |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dV = H1H 2 H3dξ1dξ2dξ3. |
|
|
|
|
|
|
|
|
|
|
|
|
(28.15) |
|||||||||||||||
Замечание 4.15 Приведёнными формулами (13.15) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
удобно пользоваться, чтобы находить коэффициенты |
|
|
|
|
|
|
gradξi |
|
|
|||||||||||||||||||||||||||||||||||||
Ламэ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e*i |
|
|||
Вывод градиента криволинейных координат |
|
|
|
|
|
|
|
|
|
|
|
|
ξ2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ r |
|||||||||||||||||||||||||||||||||
Докажем, что векторы gradξ1, gradξ2 , gradξ3 (рис. 3.15) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
x3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
образуют систему векторов, взаимных с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ1 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂r |
, |
|
∂r |
, |
|
|
|
∂r |
. |
|
|
|
|
(29.15) |
|
|
|
|
|
|
|
|
|
r |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂ξ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
∂ξ1 |
|
|
|
|
|
|
|
∂ξ3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e3 |
|
|
|
|
|
|
|||||||
Для этого нужно показать, что скалярные произведения |
|
|
|
|
|
|
e2 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 |
||||||||||||||||||||||||||||||||||||||
равны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1 |
|
|
|
||||||
gradξi |
∂r |
|
|
=1, |
gradξi |
|
|
∂r |
= 0, |
|
(i ≠ k) |
|
(30.15) |
|
|
|
|
|
|
О |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
∂ξi |
|
|
|
∂ξk |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||
Умножая обе части равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.15 К градиенту |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂r |
|
|
|
∂r |
|
|
|
|
∂r |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
d r(ξ1,ξ2 ,ξ3 ) = |
dξ1 + |
|
dξ2 + |
|
dξ3 |
|
(31.15) |
|
|
|
криволинейных координат |
|||||||||||||||||||||||||||||||||||
|
∂ξ |
|
|
|
∂ξ |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂ξ |
1 |
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
скалярно на grad ξi , мы получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
dξ |
i |
= gradξ |
i |
|
d r = (gradξ |
i |
|
|
∂r |
) dξ |
|
+ (gradξ |
i |
|
∂r |
) dξ |
2 |
+ |
(gradξ |
i |
|
∂r |
|
) dξ |
3 |
(32.15) |
||||||||||||||||||||
∂ξ |
|
∂ξ |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
∂ξ |
3 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда |
|
в |
|
|
силу |
произвольности |
d ξ1, d ξ2 , d ξ3 |
|
|
следует, |
|
|
что |
произведение |
||||||||||||||||||||||||||||||||
(gradξi |
|
∂r |
|
) равно |
единице |
|
только, |
когда |
i =1 |
, то |
|
|
есть, когда |
остаётся |
||||||||||||||||||||||||||||||||
∂ξ |
1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
90
