Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Tensor-Gotman

.pdf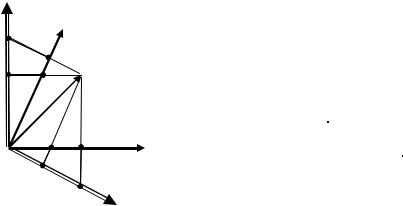

Скачиваний:

Добавлен:

09.02.2015

Размер:

1.52 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1313

Таблица 8 Компоненты тензоров в декартовых косоугольных координатах

Изображения и определения

Тензорное описание

е2

(e1,e2 ,e3 ) - реперы

a = a1 e + a2 e

+ a3 e

е2

= a e

где

a 2

a1 = a e1,

a 2 = a e2 ,

a3 = a e3 .

e 2

Векторы репера преобразуются к другой системе

координат

( e

, e

) по законам

a 1

е1

ei' = ei Bi i'

ei = ei' Ai'i

Вектор a

в этих системах имеет вид

a = aiei и a = ai'ei'

Отсюда контравариантные компоненты вектора

a преобразуются по закону

Векторы репера ei

иногда называют ковариантным

ai' = ai Ai'i

ai = ai'Bi i'

Якобиевы матрицы связаны между собой так:

базисом системы координат.

Ai'

= δ i'

и Bi

A j' = δ i

При переходе из одной системы координат к

(e1,e2 ,e3 )

- кореперы

другой ковариантные компоненты произвольного

вектора a преобразуются совершенно по другому

+ a2e

+ a3e

закону, нежели контравариантные компоненты.

a = a1e

где

= a ei , то есть,

Матрица

является обратной и

a1 = a e1,

a2 = a e2 ,

a3 = a e3

транспонированной по отношению к якобиевой

Ковариантные компоненты вектора

матрице Ai'i

преобразования x' = x'(x1, x2 , x3 )

преобразуется

по формулам

a j' = a j B j j'

Векторы репера ei

иногда называют ковариантным

базисом системы координат.

e = e A i

e = e B i'

Векторы корепера при переходе к другой системе

координат преобразуются так же, как и

контравариантные компоненты вектора a .

Определение 1. Ковариантными компонентами

вектора (или векторного поля) a

называется

система трёх чисел ai , определённая в каждой точке

пространства и в каждой системе координат, которая

a j' = a j B j' = (a1 a2 a3) b1'

b2'

b3'

при переходе от одной системы координат к другой

преобразуется по формулам

b1'

b2'

b3'

Bi i' =

∂xi

a j' = a j B j j'

где

= bi i'

∂x'i

Определение 2. Контравариантными

компонентами вектора (или векторного поля)

a 2

называется система трёх чисел a

, определённая в

= a

A i

) a

каждой точке пространства и в каждой системе

координат, которая при переходе от одной системы

координат к другой преобразуется по формулам

ai' = ai Ai'i

где Ai'i =

∂x'i

= (ai'i )

∂xi

121

Продолжение таблицы 8

dx1

dx2

dx3

∆ r

dr = ∑dxiei = dxiei = dx'k e'k

i =1

∂xi

Х3

e'k =

- переход от старого базиса к

∂x'k

новому

∂x'k

- якобиан преобразования

∂xi

k 2

Х2

Контравариантный тензор первого ранга

b = b

∂xi

= b'

вектор

Х1

∂x'

Контравариантный тензор второго ранга

T = T

eiek

= T

m'n' ∂xi

∂xk

∂x' m

∂x' n

∂x' m

∂x' n

m'n'

- компоненты этого

∂xl

∂x j

тензора

Ковариантные компоненты тензора 2 –го

ранга при переходе от нового базиса к

старому

∂xk'

∂xl'

∂xi ∂xm

k'l'

Смешанные компоненты

тензора более

высокого порядка.

T 'r sp

∂xr ∂xn ∂xq

T mnq

∂xm ∂x' s ∂x' p

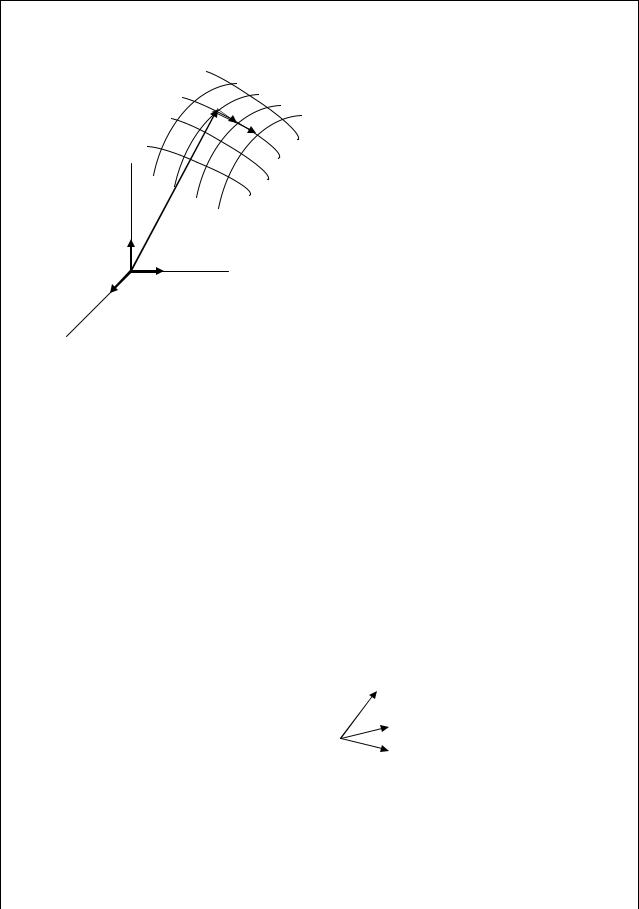
T = T

ik...m

eiek ...em

Подобная система

координат соответствует

каждому из обозначений

ei ,ek или em

T = T

i k

Каждой паре базисных векторов

meiek ...e

соответствуют зависимости

eiek = gik , eiek = g ik ,

enem = δnm

Выражение компонент фундаментального

тензора через производные радиуса-вектора

gij =

∂r

= ei e j

∂x j

∂xi

122

Таблица 9. Символы умножения и дифференцирования в тензорном исчислении

Наименование

Обозначение

Использование

Символ Кронекера

При скалярном

δij

1 когда i = j

произведении

направляющих косинусов

0 когда i ≠ j

i'≠ j',

∑αim' αmj' =

δi'j'

i' = j'.

m=1

Символ Леви – Чевита

εijk

При векторном

εijk

= 1, если значения индексов

i, j, k

образуют чётную

произведении векторов

εijk a jbk = ci

перестановку из чисел 1,2,3

−δiqδ jp ;

= - 1, если значения индексов

εijk εkpq = δipδ jq

i, j, k

образуют нечётную

перестановку из чисел 1,2,3

= 0, если значения индексов

i, j, k

не образуют

перестановки из чисел 1,2,3

(если есть равные индексы)

Символ Кристоффеля 1 –

Гi, j k

= e i

∂e j

При разложении векторов

го рода

∂e j

∂ x

по векторам

∂ xk

взаимного базиса

Символ Кристоффеля 2-

Гij k =ei

∂e

При разложении векторов

го рода

∂e j

∂ x

по векторам основного

∂ xk

базиса

Связь символа

∂ gi k

= Гi,k l

+ Гk,i l .,

Кристоффеля 1-го рода с

∂ xl

метрическим тензором

Таблица 10 Примеры, используемые в механике сплошной среды

Внешнее

Внутреннее произведений

произведение

Индексные обозначения

Символьные обозначения

aibi

a b

ai Eik

ai Eik = fk

a E = f

ai Eli = hl

E a = h

Eij Fkm

Eij F jm = Glm

E F = G

Eij Ekm

Eij Eim = Blm

E E = (E )2

Eij Fkm

Eij Fij

E; F

Eij Ekm E pq

Eij E jm Emq

(E )3

123

Таблица 11 Основные обозначения

№

Символ

Значение

∂o

Производная по времени

∂ j

Производная по

j - той координате

υk,k

Лапласиан скорости

υl

Дивергенция вектора скорости

Дивергенция вектора напряжений

p ;k

(i, k =1,2,3)

Квадратная форма трёхмерного

пространства

a;b или

a b

Диадное (неопределённое) произведение

D = a1;b1 + a2;b2 +... + a N ;b N

Диадик

ab:cd = (a c) (b d)

Формула дважды скалярного произведения

a; b × c; d = (a ×b)(c d) = h

Дважды смешанное произведение (вектор)

a; b × c; d = (a b)(c ×d) = g

Дважды смешанное произведение (вектор)

a; b ×× c; d = (a ×b)(c ×d) = uw -

Дважды векторное произведение (диада)

∂a

≡ ai ; k

Ковариантная производная ковариантного

∂ xk

вектора

∂a

∂e j

(в локальной системе координат)

+ a

i; k

∂ x

∂a

e i

≡ ai

; k

Ковариантная

производная

∂ x

контравариантного вектора

ai ; k

∂a

e i =

∂a i

+ a j

∂e j

e i

(в локальной системе координат)

∂ x

Гij k , ( Гij k

=ei

∂e j

)

Символы Кристоффеля 2-го рода

∂ xk

Гi, j k , ( Гi, j k = e

∂e j

)

Символы Кристоффеля 1-го рода

i ∂ xk

∂Ti k

Гm −T

Гm ,

−T

i k ;l

∂ x

m k

i l

i m

k l

Ковариантные производные тензора 2 – го

∂T i k

T i k

+T m k Гi

+T i mГk

ранга

∂ xl

m l

∂T ik

T i

+T m Гi

−T i Гm ,.

k;l

k m l

m k l

∂ x

124

ПРИЛОЖЕНИЕ 3 Строгие определения в тензорном исчислении

Определение 1 (скаляра) Если для каждой системы координат x1, x2 , ... xn определена функция f (x1, x2 , ... xn ) , так что для системы координат x'1 , x'2 , ... x'n мы имеем свою функцию f '(x'1 , x'2 , ... x'n ) , и если при преобразовании координат

x'i = x'i (x1, x2 , ... xn ) значения этих функций в соответствующих точках совпадают

	f '(x'1 , x'2 , ... x'n ) = f (x1, x2 , ... xn ) ,
то говорят, что функция точек f (x1, x2 , ... xn ) есть и н в а р и а н т							или с к а л я р.

Определение 2 (контравариантного вектора)					Если для каждой системы координат
x1, x2 , ... xn определена совокупность функций					a1, a2 , ... an , а для системы координат
x'1 , x'2 , ... x'n	мы имеем	свою	совокупность		функций a'1 , a'2 , ... a'n , и если			при
преобразовании	координат	x'i = x'i (x1, x2 , ... xn )				эти функции	преобразуются	по
следующим формулам		n
		n	i	i
	a' i = ∑		∂x'k	ak = ∂x'k	ak	(i =1, 2, ... n)
		k =1	∂x	∂x
		k =1

то говорят, что совокупность величин a1, a2 , ... an определяет контравариантный

вектор, и величины ai называют составляющими или компонентами контравариантного вектора а.

Определение 3 (ковариантного вектора) Если для каждой системы координат x1, x2 , ... xn определена совокупность функций a1, a2 , ... an , так что для системы координат x'1 , x'2 , ... x'n мы имеем свою совокупность функций a'1 , a' 2 , ... a' n , и если

при преобразовании координат x'i = x'i (x1, x2 , ... xn )					эти функции преобразуются по
следующим формулам
n	∂x k		∂x k
a'i = ∑		ak =		ak	(i =1, 2, ... n)
a'i = ∑	∂x'i	ak =	∂x'i	ak	(i =1, 2, ... n)
k =1

то мы будем говорить, что совокупность величин a1, a2 , ... an определяет ковариантный вектор, составляющими или компонентами которого они являются.

Определение 4 (определение контравариантного тензора второго ранга)				Если для
каждой системы координат xα определена совокупность		n2 функций	Aαβ ,	которые
при преобразовании координат	xα = xα (x1, x2 , ... xn )	(α =1, 2, ... n)	испытывают

преобразования

n n		i	k				i	k
A'ik = ∑∑	∂x'		∂x'	Aαβ	=	∂x'		∂x'	Aαβ
	α		β			α		β
i =1 k =1	∂x		∂x			∂x		∂x

то эти функции определяют контравариантный тензор второго ранга, составляющими которого они являются.

125

Определение 5 (определение ковариантного тензора второго ранга) Если для каждой

системы координат	xα определена совокупность n2						функций Aαβ ,				которые при
преобразовании	координат	xα = xα (x1, x2 , ... xn ) (α =1, 2, ... n)									испытывают
преобразования	n	n
	n	n	α		β		α		β
	A'ik = ∑∑		∂x	i	∂x	k Aαβ =	∂x	i	∂x	k Aαβ
	i =1 k =1		∂x'		∂x'		∂x'		∂x'
	i =1 k =1

то эти функции определяют ковариантный тензор второго ранга, составляющими которого они являются.

Определение 6 (определение смешанного тензора второго ранга) Если для каждой

системы координат

xα определена совокупность n2 функций A

которые при

преобразовании

координат

xα = xα (x1, x2 , ... xn ) (α =1, 2, ... n)

испытывают

преобразования

n n

A'i k = ∑∑

∂x

∂x'

Aα β = ∂x

∂x'

Aα

∂x'

i =1 k =1

∂x

∂x'

∂x

то эти функции определяют ковариантный тензор второго ранга, составляющими которого они являются.

ЛИТЕРАТУРА

1.А. И. Борисенко, И.Е. Тарапов Векторный анализ и начала тензорного исчисления. М. Высшая школа, 1966.

2.Н.Е. Кочин Векторное исчисление и начала тензорного исчисления, М.,

Наука, 1965.

3.М.А. Акивис, В.В. Гольдберг Тензорное исчисление, М. Наука, 1972.

4.Б.Е. Победря Лекции по тензорному анализу. М. Московский университет. 1979.

5.Г. Корн, Т. Корн Справочник по математике (для научных работников и инженеров)

М., Наука. 1974

6.В.И. Смирнов Курс высшей математики том 3, часть 1, М., 1958.

7.Ли Дзун-Дао Математические методы в физике М.. Мир, 1965.

8..Дж. Мейз Теория и задачи механики сплошных сред, М., Мир, 1974.

Дополнительная литература

9.Ландау Л.Д., Лифшиц Е.М. Механика, М., Физматгиз, 1965.

10.Ландау Л.Д., Лифшиц Е.М. Теория упругости, М., Наука, 1965.

11.Ландау Л.Д., Лифшиц Е.М. Гидродинамика, том 6, М., Наука, 1988.

12.Седов Л.И. Введение в механику сплошных среды, М., Физматгиз, 1962.

13.Прагер В. Введение в механику сплошных сред .М., ИЛ, 1963.

14.Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика, часть 2,

М., 1963.

126

ОГЛАВЛЕНИЕ	стр
ВВЕДЕНИЕ	3
Тензоры в механике сплошных сред	3
Задача, приводящая к понятию тензора	4
ГЛАВА 1. ПОНЯТИЕ ТЕНЗОРА	5
§ 1. Основные понятия и определения.	5
Ранг тензора.	6
§ 2. Взаимное положение двух векторов	8
Проекция вектора а на единичный вектор uо	8
Косинус угла между двумя векторами	9
Первая основная задача	10
Вторая основная задача	11
§ 3. Реперы и кореперы в пространстве	12
Проекции вектора на прямоугольные координаты	12
Проекции вектора на оси пространственных координат	13
Построение взаимного базиса	13
Свойства взаимных базисов	14
Определение связи между проекциями вектора во взаимных базисах	15
§ 4 Переход от одного ортонормированного базиса к другому	16
§ 5 Ковариантные и контравариантные компоненты	20
§ 6 Индексные обозначения и соглашение о суммировании	23
Правило индексных обозначений	23
Соглашение о суммировании А. Эйнштейна	24
§ 7 Связь между ковариантными и контравариантными
компонентами вектора	27
Случай ортогональных базисов	31
Правило поднятия, опускания и переименовании индексов	32
Фундаментальный (метрический) тензор	32
Признак тензорности величин	34
Обратный тензорный признак	35
Символ Леви-Чивита	35
§ 8 Якобиан	38
ГЛАВА 2. СВОЙСТВА ТЕНЗОРОВ И ДЕЙСТВИЯ С НИМИ	41
§ 9 Свойство симметрии тензоров	41
Перестановка индексов, симметрирование и альтернирование	42
§ 10 Диады и диадики	43
Умножение вектора a на единичную диаду E	44
Диадики	45
Произведение вектора a на диадик D	45
Алгебра диадиков	45
§ 11 Произведения тензоров и свёртки	47
Свёртки	47
Общие правила свёртывания	49
Произведение тензоров и векторов	51
Произведение тензора Т на вектор а с последующим свёртыванием	51
Свёртывание по второму индексу произведения тензора Т на вектор а	52
Умножение вектора а на тензор Т	53
Геометрическая интерпретация произведения вектора а на тензор Т	53
Произведение тензоров	53

127

§ 12 Главные значения и главные направления тензора второго ранга.	54
Основные понятия	54
Определение главных направлений и главных значений тензора Tik	55
Главные значения и главные направления симметричных
тензоров второго ранга	57
Степени тензора второго ранга. Соотношения Гамильтона – Кэли	60
§ 13. Ковариантное дифференцирование тензоров	60
Ковариантный дифференциал тензора	60
Ковариантная производная вектора	61
Символы дифференцирования в тензорном исчислении	62
Символы Кристоффеля 2-го рода Гij k	62
Символы Кристоффеля 1-го рода Гi, j k	63
Связь между символами Кристоффеля 1-го и 2 –го рода
Доказательство тождеств, связывающих приведенные величины	67
Ковариантная производная тензора	68
Правила дифференцирования тензоров	68
Теорема Риччи	69
ГЛАВА 3. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ	70
§ 14 Скалярные, векторные и тензорные поля	70
Скалярное поле	70
Производная скалярной функции по направлению вектора s	70
Градиент	71
Векторное поле	72
Поток вектора	72
Дивергенция	74
Следствия из формулы Остроградского – Гаусса	75
Циркуляция вектора	76
Теорема Грина	77
Теорема Стокса	77
Ротор	79
Следствия из теоремы Стокса	79
Тензорное поле	80
Дифференцирование тензорных полей	82
Поле тензора 2-го ранга. Поток тензорного поля	83
Несколько приложений потока поля тензора 2-го ранга	83
Дивергенция тензорного поля	84
Производная тензорного поля по направлению	85
Теорема Остроградского – Гаусса в тензорном поле	85
§ 15 Основные определения и выводы коэффициентов Ламэ	87
Смысл коэффициентов Ламэ	89
Вывод дифференциалов длины дуги, площади и объёма	90
Вывод градиента криволинейных координат	90
Вывод формулы дивергенции векторного поля	91
Дивергенция единичных векторов	92
Вывод формулу ротора векторного поля а	92
Ротор базовых векторов	93
Оператор Лапласа для скалярного поля ψ	94
Коэффициенты Ламэ и дифференциальные характеристики полей
в цилиндрической системе координат	94

128

Градиент скалярного поля ψ в цилиндрической системе координат	94
Дивергенция векторного поля а в цилиндрической системе координат	94
Ротор векторного поля а в цилиндрической системе координат	94
Лапласиан скалярного поля ψ в цилиндрической системе координат	94
Градиент скалярного поля ψ в сферических координатах	95
Дивергенция векторного поля а в сферических координатах	95
Ротор векторного поля а в сферических координатах	95
Лапласиан скалярного поля ψ в сферических координатах	95
§ 16 Основные уравнения гидромеханики жидкости	95
Уравнение неразрывности несжимаемой жидкости	95
Трубка тока	96
Тензор напряжений.	97
Идеальная жидкость.	98
Дифференциальные уравнения движения жидкости	99
Уравнение движения идеальной жидкости (уравнение Эйлера)	101
Уравнение движения вязкой несжимаемой жидкости
уравнение Навье – Стокса) при µ = const	101
Закон Архимеда	103
Теорема импульса в гидродинамике	103
ПРИЛОЖЕНИЕ 1 Элементы векторной алгебры	107
ПРИЛОЖЕНИЕ 2 Сводные таблицы	109
Таблица 1 Выражение элементов полей через коэффициенты Ламе	109
Таблица 2 Элементы векторной алгебры в тензорных выражениях	110

Таблица 3 Элементы аналитической геометрии в тензорных выражениях 113

Таблица 4 Механика в тензорном выражении		115
Таблица 5	Дифференциальные операции скалярных,
векторных и тензорных полей		116
Таблица 6	Характеристики полей в разных системах координат	117
Таблица 7	Определения тензорных величин, основанные на законе
преобразования их компонент		120
Таблица 8	Компоненты тензоров
в декартовых косоугольных координатах		121
Таблица 9. Символы умножения и дифференцирования
в тензорном исчислении		123
Таблица 10 Примеры, используемые в механике сплошной среды		123
Таблица 11 Основные обозначения		124
ПРИЛОЖЕНИЕ 3 Строгие определения в тензорном исчислении		125
ЛИТЕРАТУРА		126

129

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1313

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.03.20161.17 Mб53tau_dlya_chainikov.pdf
#
21.08.20191.28 Mб26td1.doc
#
21.04.2015943.1 Кб30td11.doc
#
18.09.2019273.41 Кб0tema4_1a.doc
#
22.08.2019451.02 Кб3Tema_1_2.docx
#
09.02.20151.52 Mб55Tensor-Gotman.pdf
#
10.02.201517.73 Mб44teopiya_tanka_sergeev.djvu
#
15.04.20195.54 Mб1teoria ответы.doc
#
23.09.201924.91 Mб6teoria-ilyukhina.docx
#
10.02.20153.26 Mб21teoria.pdf
#
10.02.20151.77 Mб7teoria_na_bilety_2013.pdf