
Tensor-Gotman
.pdf
Определение 5.14 Предел отношения |
U |
|
при s → 0 называется |
производной |
||||||||||||
s |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
функции U =U (x, y, z) |
в точке M (x, y, z) |
по направлению вектора s |
и обозначается |
|||||||||||||
|
∂U |
, то есть |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∂s |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
lim |
U = |
∂U |
|
|
|
|
|
(7.14) |
|||
|
|
|
|
|
s→0 |
s |
∂s |
|
|
|
|
|
|
|||
Переходя к пределу в равенстве (6.14), получим |
|
|
|
|
||||||||||||
|
|
|
∂U |
= |
∂U |
cosα + |
∂U |
cos β + |
∂U |
cos γ |
(8.14) |
|||||
|
|
|
∂s |
|
|
|
||||||||||
|
|
|
|
∂ x |
|
∂ y |
|
|
|
∂ z |
|
|||||
Замечание 1.14 Из формулы (8.14) видно, что, зная производные скалярной функции, можно найти производную по любому направлению s .
Замечание 2.14 В данном случае берутся частные производные, потому что они имеют разные значения в зависимости от направления.
Градиент
Определение 6.14 Дифференциальной векторной характеристикой скалярного поля является градиент,
который выражается формулой
gradU = ∂U i + ∂U j + |
∂U k |
|
(9.14) |
|||
|
∂ x |
∂ y |
∂ z |
|
|
|
Т е о р е м |
а |
1.14 Пусть дано |
скалярное |
поле |
||
U =U (x, y, z) |
и в этом скалярном поле определено |
|||||
поле градиента |
gradU . |
Производная |
∂U |
по |
||
|
|
|
|
|
∂s |
|
направлению |
некоторого |
вектора |
s |
равняется |
||
проекции вектора gradU на вектор s (рис. 4.14) . |
|
|||||
Рис. 4.14 Вектор градиента
U (x, y, z) = C
so 
gradU
Рис. 4.14 К теореме 1.14
Д о к а з а т е л ь с т в о. Рассмотрим единичный вектор |
so , соответствующий вектору s |
||||||
so = i cosα + jcos β +k cosγ |
|
|
(10.14) |
||||
Скалярное произведение gradU на so : |
|
|
|
|
|
||
gradU so = |
∂U |
cosα + |
∂U |
cos β + |
∂U |
cosγ |
(11.14) |
|
|
|
|||||
|
∂ x |
∂ y |
∂ z |
|
|||
Выражение, стоящее в правой части (11.14), является производной функции U по
вектору s . Отсюда
gradU so = |
∂U |
(12.14) |
|
∂s |
|||
|
|
Если обозначить угол между gradU и s как ϕ , то можно записать скалярное произведение в виде
|
gradU |
|
|
|
so |
|
cosϕ = |
∂U |
(13.14) |
|
|
|
|
|
|||||||
∂s |
||||||||||
|
|
|
|
|
|
|
|
|
Учитывая, что модуль единичного вектора равен единице, можно написать
|
gradU |
|
cosϕ = |
∂U |
, |
(14.14) |
|
|
|
||||||
∂s |
|||||||
|
|
|
|
|
71 |
||
|
|
|
|
|
|
а отсюда видно, |
что слева стоит проекция градиента функции U на вектор s , что и |
|||||||||||||||
требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Замечание 3.14 Эта теорема устанавливает связь между производной по направлению и |
||||||||||||||||
градиентом скалярной функции U =U (x, y, z) . |
|
|
|
|
|
|
|
|||||||||
Замечание |
4.14 |
Если учесть, что нормаль к поверхности |
F(x, y, z) = 0 |
(из курса |
||||||||||||
аналитической геометрии) имеет вид |
∂ F i + |
∂ F j + |
∂ F k , |
|
|
|
|
|
||||||||
|
|
|
|
|
|
N = |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
∂ x |
|
∂ y |
∂ z |
|
|
|
|
|
|
то |
легко |
видеть, |
что |
градиент |
gradU = ∂U i + |
∂U j + |
∂U k |
является |
вектором, |
|||||||
|
|
|
|
|
|
|
|
|
∂ x |
|
∂ y |
∂ z |
|
|
|
|
направленным по нормали к поверхности равного уровня U (x, y, z) = C . (рис.4.14). |
||||||||||||||||
Векторное поле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определение 7.14 |
Векторным полем называется |
часть |
пространства, |
каждой точке |
||||||||||||
|
|
|
|
|
|
которого |
соответствует |
одно |
значение |
вектора |
||||||
|
z |
|
|
|
|
F(x, y, z) (рис. 5.14). |
|
|
|
|
|
|
|
|||
|
|
М |
|
F |
|
Определение |
8.14. |
|
Аналитически |
векторное поле |
||||||
|
r |
|
|
|
|
можно описать в виде функции координат |
|
|
||||||||
|
z |
|
|
y |
F(x, y, z) = P(x, y, z) i +Q(x, y, z) j + R(x, y, z)k |
|
(15.14) |
|||||||||
|
|
|
|
или радиуса вектора |
F(r) = P(r) i +Q(r) j + R(r) k |
|
||||||||||
|
О |
|
y |
|
|
|||||||||||
|
|
|
|
Замечание 5.14 Если скалярное поле определяется одной |
||||||||||||
|
x |
|
|
|
|
|||||||||||
|
|
|
|
|
функцией, то векторное поле определяют три функции |
|||||||||||
|
|
|
|
|
|
|||||||||||
|
x |
|
|
|
|
координат: P (x, y, z) ,Q (x, y, z) , R (x, y, z) . |
|
|
||||||||
Рис. 5.14 К заданию векторного |
Определение |
9.14. |
Основными |
характеристиками |
||||||||||||
|
поля |
|
|
|
векторного |
|
поля |
являются |
поток, |
дивергенция, |
||||||
|
|
|
|
|
|
циркуляция, ротор |
|
|
|
|
|
|
|
|||
Поток вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рассмотрим поле вектора F(r) , имеющего |
|
|
F |
|
|||||
|
|
|
|
|
||||||
компоненты P(r),Q(r), R(r). . Примерами векторных |
|
|
|
|
||||||
полей могут служить поле скоростей, поле ускорений, |
|
|
|
|
||||||
силовое поле (рис. 6.14). |
|
|
|
|
|
|
|
|||
Определение 10.14. Потоком векторного поля через |
|
|
|
|
||||||
поверхность называется поверхностный интеграл, |
|
|
|
|
||||||
взятый от скалярного произведения |
вектора поля |
|
|
Рис. 6.14 Поток вектора F |
||||||
F (r) на вектор нормали: |
|
|
|
|
|
|||||
|
|
|
|
Π = ∫∫F n dσ = ∫∫Fn dσ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
v |
|
|
S |
S |
|
|
|
|
|
|
|
|
|
|
(16.14) |
|
|
|
|
|
|
|
|
|
|
|
|
|
физический смысл |
|
|
|
|
n |
Для |
того, |
чтобы представить |
себе |
этого |
|||
|
S |
выражения, рассмотрим рис. 7.14. Если векторное поле представляет |
||||||||
|
|
собой поле скоростей жидкости v , и если построить параллелепипед, |
||||||||
|
|
|
||||||||
|
v |
S |
высота которого равна проекции вектора скорости на нормаль n к |
|||||||
|
|
|||||||||
|
|
поверхности |
S , |
а основание равно малому элементу площади |
||||||
|
|
|
||||||||
|
Рис. 7.14 Элемент |
поверхности |
S , |
через которую. |
идёт поток вектора скорости, то |
|||||
|
потока |
объём этого параллелепипеда равен объёму жидкости, протекающей |
||||||||
|
через |
элемент |
поверхности |
|
S |
в одну секунду и |
равен |
|||
|
|
|
|
|||||||
72
V = v n S . Если взять интеграл по поверхности, то получим количество жидкости,
протекающей в секунду через эту поверхность.(расход)
Если обобщить этот интеграл на произвольное векторное поле F (r) , то получится
выражение (16.14)
Замечание 6.14 Если поверхность S замкнута и охватывает объём V, то количество жидкости, протекающей в секунду через поверхность S , равно суммарной мощности источников и стоков, находящихся в объёме V.
Определение 11.14 Пространственная область V , ограниченная двумя кусочно гладкими поверхностями Σ1 и Σ3 , заданными в виде
z1 = z1(x, y) и z3 = z3 (x, y)
(17.14)
ибоковой цилиндрической поверхностью Σ2 с
образующими, параллельными оси Oz , называются |
« z − |
||||||||||
цилиндрической областью» (рис. 8.14). |
|
|
|
|
|
|
|||||
Поверхности |
z1 = z1 (x, y) |
|
и z3 = z3 (x, y) |
- |
это |
||||||
криволинейные |
основания |
(нижнее |
и |
|
верхнее) |
« z − |
|||||
цилиндрической области». |
|
|
|
|
|
|
|
|
|
|
|
Замечание 7.14 |
Аналогично |
можно |
построить |
« x |
- |
||||||
цилиндрическую» и « у – цилиндрическую» области. |
|
|
|||||||||
|
|
|
|
∂ P |
|
∂Q |
|
∂ R |
|
|
|
Рассмотрим в |
интеграле |
|
|
+ |
+ |
|
третье |
||||
∫∫∫ |
∂ x |
∂ y |
∂ z |
dV |
|||||||
|
|
V |
|
|
|
|
|
|
|||
z Σ3 |
n |
n
Σ2
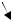 n Σ1
n Σ1
0
y
x D
Рис. 8.14 К формуле Остроградского - Гаусса
слагаемое и преобразуем его к разности двойных интегралов, взятых по области D
|
∂ R |
|
Σ3 |
∂ R |
|
|
|
||
|
|
|
|
|
|
|
|||
∫∫∫ |
|
dV = ∫∫ |
∫ |
|
dz dxdy = ∫∫[R(x, y, z3 (x, y)) − R(x, y, z1(x, y))]dxdy = |
||||
∂ z |
∂ z |
||||||||
V |
S |
|
Σ |
|
S |
D |
|||
|
|
|
D |
1 |
|
|
|
||
= ∫∫R(x, y, z3 (x, y)) dxdy − ∫∫R(x, y, z1(x, y)) dxdy |
|||||||||
SD |
|
|
|
|
|
SD |
|
||
Первый из полученных интегралов можно свести к поверхностному интегралу, взятому по верхней поверхности Σ3 с уравнением z = z3 (x, y) , а второй – по нижней поверхности
Σ3 с уравнением z = z1 (x, y) . Отсюда, с учётом направления внешней нормали к поверхностям Σ1 и Σ3 , можно записать
∫∫∫V ∂∂Rz dV = Σ∫∫3 R(x, y, z) dxdy + Σ∫∫1 R(x, y, z) dxdy
где первый интеграл берётся по верхней стороне поверхности Σ3 , а второй по нижней стороне поверхности Σ3 . Прибавим такой же интеграл по поверхности Σ2 . Этот интеграл равен нулю, так как нормаль перпендикулярна оси z , в направлении которой берётся интеграл, то есть ∫∫Σ2 R(x, y, z dxdy = 0 . Поэтому можно записать
∫∫∫V ∂∂Rz dV = Σ∫∫3 R(x, y, z) dxdy + Σ∫∫2 R(x, y, z) dxdy + Σ∫∫1 R(x, y, z) dxdy =
=∫∫R dxdy =∫∫R cos(n, z) dσ
ΣΣ
или
73
|
|
∫∫∫ |
∂ R dV = |
∫∫R cos(n, z) dσ |
|
||||
|
|
|
V |
∂ z |
|
|
Σ |
|
|
|
|
|
|
|
|
|
|
||
Аналогично получаются интегралы |
|
|
|||||||
|
|
∫∫∫ |
∂Q dV = |
∫∫R cos(n, y) dσ, |
|
||||
|
|
|
V |
∂ y |
|
|
Σ |
|
|
|
|
|
|
|
|
|
|
||
|
|
∫∫∫ |
∂ P dV = |
∫∫R cos(n, x) dσ |
|
||||
|
|
|
V |
∂ x |
|
|
Σ |
|
|
Отсюда можно записать |
|
|
|
|
|
||||
|
∂ P |
|
∂Q |
|
∂ R |
|
|
|
|
|
+ |
+ |
|
|
(18.14) |
||||
∫∫∫ |
∂ x |
|
∂ y |
∂ z |
dV = ∫∫(P cosα +Q cos β + R cosγ )dS |
||||
V |
|
|
|
|
S |
|
|||
где F = P i +Q j+ R k , а n =i cosα + jcos β + k cosγ .
Это и есть формула Остроградского - Гаусса в координатной форме. Она связывает
тройной интеграл по замкнутой пространственной области с поверхностным интегралом, взятом по внешней стороне поверхности, ограничивающей эту область.
Для вывода этого выражения в векторной форме введём понятие дивергенции векторного поля.
Замечание 8.14 Поток векторного поля является скалярной величиной.
Замечание 9.14 Если представить векторное поле как поле скоростей движущейся жидкости, то поток П выражает объём жидкости, протекающей через поверхность S в единицу времени. (расход).
Рис. 9.14 Источник и сток |
Дивергенция
Определение 12.14 Дивергенцией векторного поля называется предел отношения потока П через замкнутую поверхность S к объёму V , ограниченного этой поверхностью, когда объём V стремится к нулю
∫∫F n dS
div F = lim S
V→0 V
(за V принимаем бесконечно малый объём ).
Т е о р е м а 2.14 Если F = P(x, y,z)i + Q(x, y,z)j + R(x, y,z)k - векторное поле,
определённое в области V и такое, что функции P,Q, R непрерывны в V вместе со всеми производными первого порядка, то div F существует во всех точках этой
области и в любой декартовой системе координат выражается формулой
div F = |
∂ P |
+ |
∂Q |
+ |
∂ R |
(19.14) |
|
∂ x |
∂ y |
∂ z |
|||||
|
|
|
|
Д о к а з а т е л ь с т в о. Воспользуемся формулой (18.14), которую представим в виде
|
|
|
|
∂ P |
|
∂Q |
|
∂ R |
|
|
|
|
|
+ |
+ |
|
|||
Π = ∫∫F n dσ = ∫∫(P cosα +Q cos β + R cosγ )dS = ∫∫∫ |
∂ x |
∂ y |
∂ z |
dV |
|||||
S |
S |
V |
|
|
|
|
|||
Тогда
|
|
|
∂ P |
|
∂Q |
|
∂ R |
|
|
|
|
|
+ |
+ |
|
|
|||
|
∫∫∫ |
∂ x |
∂ y |
∂ z |
dV |
|
|||
div F = lim |
V |
|
|
|
|
. |
|||
|
|
|
|
V |
|
|
|
||
V →0 |
|
|
|
|
|
|
|
||
74

Производная |
|
в |
|
правой части существует и равна производной |
от интеграла |
||||||
|
∂ P |
|
∂Q |
|
∂ R |
|
|
|
|
||
|
+ |
+ |
|
|
|
|
|||||
∫∫∫ |
∂ x |
∂ y |
∂ z |
dV по объёму, которая по теореме о среднем для тройного интеграла |
|||||||
V |
|
|
|
|
|
|
|||||
|
|
∂ P |
|
∂Q |
|
∂ R |
|
|
|
||
|
|
+ |
+ |
|
V , где А – некоторая средняя точка в объёме V |
При стягивании |
|||||
равна |
∂ x |
∂ y |
∂ z |
|
|||||||
|
|
|
|
A |
|
|
|||||
объёма в точку получим, что div F = ∂∂Px + ∂∂Qy + ∂∂Rz , что и требовалось доказать.
Замечание 10.14 В гамильтоновом обозначении дивергенция представляет собой
скалярное произведение |
оператора |
Гамильтона = |
∂ |
i + |
∂ |
|
j + |
∂ |
k |
на векторную |
||||||||||||
∂ x |
∂ y |
∂ z |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
функцию F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F = ( |
∂ |
i + |
∂ |
j + |
∂ |
k) (Pi + Qj + Rk) = |
∂P |
+ |
∂Q |
|
+ |
∂R |
|
= div F |
|
(20.14) |
||||||
∂ x |
∂ y |
∂ z |
∂ x |
∂ y |
∂ z |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Подставляя (19.14) в формулу (18.14) и учитывая (16.14), можно поток выразить через дивергенцию следующим образом:
Π = ∫∫∫div F dV = ∫∫F n dσ |
(21.14) |
|
V |
Σ |
|
Замечание 11.14 (21.14) - это формула Остроградского – Гаусса в векторном виде.
Замечание 12.14 Дивергенция векторного |
поля F |
является |
дифференциальной |
||||||||||
скалярной характеристикой векторного поля. |
|
|
|
|
|
|
|
||||||
Расчётные формулы дивергенции имеют вид: |
|
|
|
|
|
|
|
||||||
div F = |
∂ P |
+ |
∂Q |
+ |
∂ R |
или |
F = |
∂ P |
+ |
∂Q |
+ |
∂ R |
(22.14) |
|
∂ y |
∂ z |
|
∂ y |
∂ z |
||||||||
|
∂ x |
|
|
|
∂ x |
|
|
||||||
Замечание 13.14 Дивергенция выражает интенсивность источника (или стока) в точке
M (x, y, z) векторного поля (рис. 9.14).
Определение 13.14 Поток можно рассматривать как суммарную мощность источников и стоков, находящихся в данном объёме, ограниченном поверхностью S (формула 21.14) Таким образом, формула Остроградского – Гаусса имеет вид
∫∫∫div F dV = ∫∫F n dσ |
(23.14) |
|
V |
S |
|
Следствия из формулы Остроградского – Гаусса |
|
|
В гамильтоновых обозначениях формула (23.14) имеет вид: |
|
|
∫∫∫ a dτ = ∫∫n a dS |
(24.14) |
|
V S
Эта формула справедлива для случая векторного произведения (для ротора)
∫∫∫ ×a dτ = ∫∫n ×a dS |
(25.14) |
VS
Вслучае скалярной функции ϕ эта формула имеет такую же форму
∫∫∫ ϕ dτ = ∫∫nϕ dS |
(26.14) |
V S
Из (24.14) и (25.14) следует, что формула (24.14) сохраняет свой вид для диадного произведения двух векторных функций
75

∫∫∫ (v;a) dτ = ∫∫n( v;a) dS |
(27.14) |
|
V |
S |
|
Формула (24.14) при применении к скалярному произведению двух векторных функций имеет вид:
∫∫n( a v) dS = ∫∫∫[a( v) + (v )a]dτ |
(28.14) |
|
S |
V |
|
Для лапласиана это соотношение преобразуется следующим образом:
|
|
|
∫∫∫ 2 ϕ dτ = ∫∫∫ ( ϕ ) dτ = ∫∫(n )ϕ dS = ∫∫ |
∂∂ϕn dS |
(29.14) |
||||||||
|
|
|
V |
|
V |
|
|
S |
|
S |
|
|
|
Применительно к векторной функции получается формула |
|
|
|
|
|||||||||
|
|
|
|
|
∫∫(n )a dS = ∫∫∫ 2 a dτ |
|
|
(30.14) |
|||||
|
|
|
|
|
S |
|
|
V |
|
|
|
|
|
Циркуляция вектора |
|
|
|
|
|
|
|
|
|||||
|
В векторном поле а рассмотрим некоторую кривую М1М2 .(Рис.10.14) и разобьем её с |
||||||||||||
помощью |
точек |
r1,r2 ,...,rn |
на |
малые |
участки |
|
|
t |
|
||||
ri |
= ri |
−ri −1 . Составим сумму произведений |
|
|
|
|
|||||||
|
|
|
a |
|
|||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
dL |
|
|
|
|
|
|
|
∑ai ri , |
|
|
(31.14) |
|
dL |
|
||
|
|
|
|
|
|
|
|
|
|
||||
где |
ai |
|
|
|
i =1 |
|
|
|
|
M2 |
ri |
L |
|
– значение вектора поля в какой-нибудь точке |
|
||||||||||||
|
|
||||||||||||
участка |
ri . |
|
|
Если существует |
предел |
суммы |
|
ri ri−1 |
M1 |
|
|||
Определение 14.14 |
|
|
|
|
|||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ai |
ri |
при |
неограниченном |
возрастании |
числа |
Рис. 10.14 К циркуляции |
|
||||||
i =1 |
|
|
|
|
|
|
|
|
|
|
вектора |
|
|
|
|
ri |
|
|
|
|
|
|
|
|
|
|
|
элементов |
и |
убывании |
до |
нуля |
длины всех |
|
|
|
|
||||
|
|
|
|
||||||||||
элементов, то он называется криволинейным интегралом вдоль М1М2 и обозначается
|
n |
∫a dr = |
∫a1dx1 + a2dx2 + a3dx3 |
|
lim |
∑ai ri = |
(32.14) |
||
n→∞ i =1 |
M1M 2 |
M1M 2 |
|
|
Здесь вектор dr направлен в каждой точке кривой М1М2 по касательной, и его модуль равен дифференциалу дуги кривой:
dr = dx2 |
+ dx2 |
+ dx2 |
= dL |
(33.14) |
1 |
2 |
3 |
|
|
Определение 15.14 Криволинейный интеграл по замкнутому контуру называется циркуляцией вектора а по контуру L и обозначается в виде
Γ = ∫a dL |
(34.14) |
L |
|
Здесь dL - направленный элемент контура, который равен dL = t dL ( t - орт касательной к
контуру, dL - дифференциал длины дуги контура). Замечание 14.14 Если а – сила, то циркуляция представляет собой работу этой силы при движении по контуру.
|
x2 |
x2 |
=ϕ2 (x1 ) |
|
|
|
|
|
|||
|
|
|
β |
|
|
|
|
А |
σ |
В |
|
|
|
α |
|
|
|
|
|
|
|
|
|
О |
|
x2 |
= ϕ1 |
(x1 ) |
x1 |
|
a |
|
b |
||
|
|
|
|
||
Рис. 11.14 К теореме Грина
76
Теорема Грина |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пусть задано векторное поле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
F (x1, x2 , x3 ) = P(x1, x2 , x3 ) +Q(x1, x2 , x3 ) + R(x1, x2 , x3 ) |
(35.14) |
|||||||||||||||||||||||||||||
и заданы |
|
∂ P |
; |
∂ P |
; |
∂Q |
; |
∂Q |
|
; |
∂ R |
; |
∂ R |
. |
|
|
|
|
||||||||||||
|
|
|
|
|
∂ x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
∂ x |
2 |
|
∂ x |
3 |
|
∂ x |
3 |
|
|
∂ x |
∂ x |
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
Т е |
о |
|
р е |
м |
|
а |
|
3.14 |
|
Пусть |
на |
плоскости заданы непрерывные |
функции |
|||||||||||||||||
P(x , x |
2 |
),Q(x , x |
2 |
) |
и их производные |
|
|
∂ P |
и |
∂Q |
. Тогда справедлива формула |
|||||||||||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ x3 |
|
∂ x1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂Q |
|
|
|
∂ P |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
(36.14) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ |
∂ x |
∂ x |
2 |
dσ = ∫Pdx1 + Qdx2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
1 |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Д о к а з а т е л ь с т в о. Двойной интеграл может быть представлен в виде двукратного интеграла. Для примера рассмотрим интеграл (рис. 11.14)
|
|
|
|
|
|
|
|
|
|
|
|
|
dx1dx2 = ∫b dx1 |
ϕ |
( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∫∫ |
∂ P |
dσ = ∫∫ |
∂ P |
|
|
2∫ |
1 |
∂ P |
|
dx2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
∂ x2 |
∂ x2 |
|
|
∂ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
σ |
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
a |
|
ϕ1( x1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ∫b [P(x1 ,ϕ2 (x1 )) − P(x1 ,ϕ1 (x1 ))]dx1 = |
∫P(x1 , x2 )dx1 − |
|
∫P(x1 , x2 )dx1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AαB |
|
|
|
|
|
|
|
|
|
|
AβB |
|
|
|
|
|
|
|
|
|
|
|
||||||
Меняя в первом интеграле направление интегрирования, получим |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
∫∫∂∂xP2 |
dσ = − ∫P(x1 , x2 )dx1 − |
∫P(x1 , x2 )dx1 = −∫P(x1 , x2 ) dx1 |
|
|
|
(37.14) |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
BαA |
|
|
|
|
|
AβB |
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Аналогично получается |
∫∫∂∂xQ dσ = ∫Q dl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(38.14) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
1 |
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вычитая из (38.14) равенство (37.14), получим формулу Грина |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂Q |
|
∂ P |
|
|
|
|
|
|
∫Pdx1 + Qdx2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(39.14) |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ |
∂ x |
− ∂ x |
2 |
dσ = |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
1 |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Теорема Стокса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ P |
|
∂ P |
|
∂Q |
|
||||||||||||
Т е о р е м а 4.14 Если функции |
|
P(x |
, x |
2 |
, x |
3 |
),Q(x |
, x |
2 |
, x |
3 |
), R(x , x |
2 |
, x |
3 |
) и |
, |
, |
, |
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
∂ x2 |
|
∂ x3 |
∂ x1 |
|||||||||
|
∂Q |
|
∂ R |
|
∂ R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
, |
, |
|
непрерывны на поверхности |
S |
и на замкнутом контуре |
L , который |
||||||||||||||||||||||||||||||||||||||||||
|
∂ x |
|
∂ x |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
∂ x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
является границей S , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
∫∫ |
|
∂ R |
|
∂Q |
|
|
|
|
|
|
|
|
|
∂ P |
∂ R |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
∂ x |
2 |
∂ x |
cos(n, x1 ) + |
|
|
∂ x |
− ∂ x |
cos(n, x2 ) + |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
|
|
|
(40.14) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
∂Q |
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
+ |
|
− |
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
∂ x1 |
|
cos(n, x3 ) dS = ∫Pdx1 +Qdx2 + Rdx3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ x2 |
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где n - орт нормали к поверхности S .
Поверхность S считается двусторонней, а положительное направление нормали n на ней связано с направлением обхода контура L .
77
Определение 16.14 Положительный обход контура L выбирается так, чтобы поверхность всегда оставалась слева для наблюдателя, обходящего контур так, что положительный орт n в точках у контура L направлен от ног к голове наблюдателя.
Д о к а з а т е л ь с т в о. Доказательство теоремы Стокса основано на теореме Грина (которая относится к плоскости).
За положительный обход контура L принимается направление против часовой стрелки. В этом случае орт n составляет с осью x3 острый угол. Тогда
dσ12 = dS cos(n, x3 ) при cos(n, x3 ) > 0
Преобразуем интеграл
 ∫P(x1 , x2 , x3 ) dx1 ,
∫P(x1 , x2 , x3 ) dx1 ,
L
используя тот факт, что контур L принадлежит поверхности S , уравнение которой может быть записано в виде x3 = f (x1, x2 ) . Отсюда при переходе от пространственного
контура интегрирования L к плоскому l подынтегральная функция может быть записана в виде P[x1, x2 , f (x1, x2 )] . Эта функция содержит только две координаты x1, x2 , которые
для переменной точки на контуре L имеют те же значения, что и в соответствующей точке на контуре l . Таким образом, получается равенство
∫P(x1, x2 , x3 ) dx1 = ∫P[x1, x2 , f (x1, x2 )] dx1 .
|
|
|
L |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
Применяя к этому интегралу формулу Грина, получим |
|
|
|
|
|
|
|||||||||||||||
∫P[x1, x2 , f (x1, x2 )]dx1 = |
|
|
|
|
|
|
|
|
|
||||||||||||
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − ∫∫ |
|
∂ P[x1 |
, x2 , |
|
f (x1, x2 )] + |
∂ P[x1, x2 , f (x1, x2 )] ∂ f |
|
|
|
(41.14) |
|||||||||||
|
|
dσ12 |
= |
|
|||||||||||||||||
|
σ12 |
|
|
|
|
|
∂x2 |
|
|
|
∂ f |
∂x2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= − ∫∫ |
|
∂ P[x1 |
, x2 , f (x1, x2 )] + |
∂ P[x1, x2 , f (x1, x2 )] ∂ f |
|
|
|
|
|
||||||||||||
|
cos(n, x3 )dS |
|
|
|
|||||||||||||||||
|
σ12 |
|
|
|
|
|
∂x2 |
|
|
|
∂ f |
∂x2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Косинусы углов, которые составляет внешняя нормаль n к поверхности x3 |
= f (x1, x2 ) |
||||||||||||||||||||
с координатными осями, имеют выражения |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
cos(n, x1) = ± |
|
|
|
p |
|
|
, |
|
|
|
x3 |
|
|
l |
|
||||||
|
1 + p2 + q2 |
|
|
|
|
σ23 |
n |
|
|||||||||||||
cos(n, x2 ) = |
|
|
|
q |
|
|
, |
(42.14) |
|
|
|
S |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 + p2 + q2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
± |
|
|
|
|
|
|
|
|
|
|
|||||||
cos(n, x3 ) = |
|
|
|
1 |
|
|
, |
|
|
О |
L |
|
x2 |
|
|||||||
|
1+ p2 + q2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
± |
|
|
|
|
|
|
|
|
|
|
|||||||
где p = |
∂ f |
, q = |
∂ f |
|
и |
|
∂ f |
=1. |
|
|
|
|
σ12 |
|
|
|
|||||
∂ x |
∂ x |
2 |
|
∂ x |
3 |
|
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
cos(n, x2 ) на |
|
x1 |
|
|
|
|
|
||||
Если умножить в этих формулах |
|
|
|
|
|
|
|||||||||||||||
cos(n, x3 ) и cos(n, x3 ) - на cos(n, x2 ) |
и приравнять |
|
Рис. 12.14 К выводу формулы |
|
|||||||||||||||||
правые части равенств |
|
|
|
|
|
|
|
|
|
Стокса |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
78

|
∂ f |
|
cos(n, x3 ) |
|
|
|
|
|
|
||
cos(n, x2 ) cos(n, x3 ) = |
∂ x2 |
и cos(n, x3 ) cos(n, x2 ) = |
|||
± |
1 + p2 + q2 |
||||
|
|
||||
то с учётом направления касательных к проекциям контура координатные плоскости (рис. 12.14) получим равенство
∂∂xf3 cos(n, x3 ) = −cos(n, x2 )
Тогда формула (41.14) примет вид
∫P dx1 |
|
|
∂ P cos(n, x3 ) − |
|
|
= −∫∫ |
∂ P cos(n, x2 ) dS . |
||||
L |
S |
|
∂x2 |
∂x3 |
|
|
|
|
|
||
cos(n, x2 ) ,
± 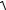 1 + p2 + q2
1 + p2 + q2
L на соответствующие
(43.14)
(44.14)
Аналогично получаются интегралы
|
|
|
∂Q |
cos(n, x1) − |
∂Q |
|
|
||
∫Q dx2 = −∫∫ |
∂x |
|
∂x |
cos(n, x3 ) dS , |
(45.14) |
||||
L |
S |
|
|
3 |
|
|
1 |
|
|
|
|
|
∂ R |
cos(n, x2 ) − |
∂ R |
|
|
||
∫R dx3 = −∫∫ |
∂x |
|
∂x |
|
cos(n, x1) dS . |
(46.14) |
|||
L |
S |
|
1 |
|
|
2 |
|
|
|
Складывая эти формулы, получим формулу Стокса (40.14)
|
|
|
|
|
|
|
|
∂ R |
|
∂Q |
|
|
∂ P |
|
∂ R |
|
|||
|
|
|
|
|
|
|
|
− |
|
|
− |
|
|||||||
∫Pdx1 + Qdx2 + Rdx3 = ∫∫ |
∂ x |
2 |
∂ x |
3 |
cos(n, x1) + |
∂ x |
3 |
∂ x |
cos(n, x2 ) + |
||||||||||
L |
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
1 |
|
|||
|
∂Q |
|
∂ P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
+ |
∂ x |
∂ x |
2 |
cos(n, x3 ) dS |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
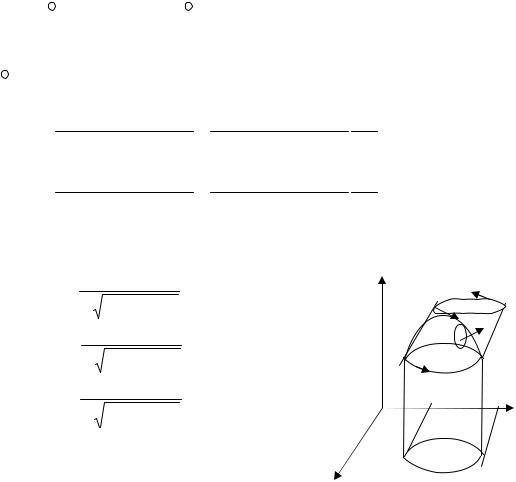
Ротор
Для представления формулы Стокса в векторном виде необходимо ввести понятие ротора. Ротор векторного поля F равен векторному произведению оператора Гамильтона
на F , то есть, rot F = ×F .
|
i |
|
j |
|
rot F = |
∂ |
|
∂ |
|
∂x |
|
∂x |
2 |
|
|
|
|||
|
1 |
|
|
|
|
P |
|
Q |
|
k
∂
∂x3
R
|
∂ R |
|
∂Q |
|
|
∂ P |
|
∂ R |
|
|
∂Q |
|
∂ P |
|
|
|||||
|
− |
|
|
− |
|
|
− |
|
(47.14) |
|||||||||||
∂ x |
|
∂ x |
|
∂ x |
|
∂ x |
∂ x |
∂ x |
|
|||||||||||
= |
2 |
3 |
i + |
3 |
j + |
2 |
k |
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|||||
Единичный вектор нормали имеет вид
n = i cos(n, x1) + jcos(n, x2 ) +k cos(n, x3 )
Легко видеть, что произведение
|
∂ R |
|
∂Q |
|
|
∂ P |
|
∂ R |
|
|
∂Q |
|
∂ P |
||||
|
− |
|
|
− |
|
|
− |
||||||||||
∂ x |
|
∂ x |
∂ x |
|
∂ x |
∂ x |
∂ x |
|
|||||||||
rot F n = |
2 |
cos(n, x1) + |
3 |
|
cos(n, x2 ) + |
2 |
|||||||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
||||
Тогда получается формула Стокса в векторной форме
 ∫F dl = ∫∫rot F n dS ,
∫F dl = ∫∫rot F n dS ,
(48.14)
cos(n, x3 )
(49.14)
(50.14)
L S
т.е. циркуляция вектора по замкнутому контуру равна потоку ротора этого вектор через любую поверхность, на которой может лежать этот контур.
79

Следствия из теоремы Стокса
Формулу (44.14) можно применить не только к векторной, но и к скалярной функции. В этом случае она имеет вид:
∫ϕ dl = ∫∫(n × )ϕ dS |
(51.14) |
LS
Вслучае векторного произведения вектора дифференциала длины дуги d l на вектор a
формула Стокса имеет вид:
 ∫dl ×a = ∫∫(n × ) a dS = −∫∫n( a ) dS + ∫∫( ;a )n dS
∫dl ×a = ∫∫(n × ) a dS = −∫∫n( a ) dS + ∫∫( ;a )n dS
L |
S |
|
S |
S |
|
или, если учесть, что диадное произведение ( ;a )n = (n )a , получим равенство |
|
||||
|
∫dl ×a = −∫∫n( a ) dS + ∫∫(n )a dS |
(52.14) |
|||
|
L |
S |
|
S |
|
Тензорное поле
Определение 17.14. Говорят, что задано тензорное поле, если каждой точке пространства x и каждому моменту времени t сопоставлен тензор Т( r , t ) , где радиус -
вектор r меняется в заданной области пространства, а t |
- в заданном интервале времени. |
||||
Частными случаями |
тензорных |
полей |
являются |
скалярные |
или векторные поля |
ϕ = ϕ(r) или a = a(r) . |
|
|
|
|
|
Примеры скалярных |
полей: 1) |
поле |
давления |
p = p(r) , |
2) поле температуры |
T = T (r) , 3) плотность ρ = ρ(r) .
Примеры векторных полей: 1) поле скорости v = v(r) , 2) поле ускорений w = w(r) Пример тензорного поля – напряжённое состояние среды pik = pik (r)
Определение 18.14 Тензорное поле называется непрерывным (или дифференцируемым), если компоненты Т(x,t) являются непрерывными (или
дифференцируемыми) функциями x(x1, x2 , x3 ) и t .
Определение 19.14 Если компоненты тензора зависят только от x , то тензорное поле называется стационарным.
Определение 20.14 Тензорным полем n -го ранга Ti1i2 ...in (x1, x2 , x3 ) называется
совокупность 3n функций, которые в любой точке пространства (x1, x2 , x3 ) образуют
тензор n -го ранга.
1) Случай n = 0 даёт скалярное поле, то есть скалярную функцию координат Φ(r)
Примером скалярного поля служит поле точечного электрического заряда Φ(r) = e r Величина
|
|
|
n |
1 2 |
|
r |
|
= |
∑xi2 |
|
(53.14) |
|
|||||
|
|
i =1 |
|
|
|
- скаляр, поэтому функция Φ(r) инвариантна относительно вращения.
2) Случай n =1: векторное поле a(r) - векторная функция векторного аргумента.
Примером может служить электрическое поле точечного заряда E = r e r 2 .
80
