
Tensor-Gotman
.pdf
Произведение тензоров и векторов
Тензор символически записывается в виде
|
|
|
|
|
|
t11 |
t12 |
t13 |
|
|
t11 |
t12 |
|
|
|
|
|
|
|
||||||
|
Tik |
|
|
|
= |
t21 |
t22 |
t23 |
|
или |
T = t21 |
t22 |
|
|
|
|
|||||||||
|
|
|
|
|
|
t31 |
t32 |
t33 |
|
|
|
t32 |
|
|
|
|
|
|
|
|
t31 |
Вектор записывается в виде
a = e1a1 +e2a2 + e3a3.
t13
t23 (11.11)
t33
(12.11)
Каждый тензор второго ранга можно представить в подобном виде, то есть, в виде трёх векторов или записать его как сумму трёх диад (диадика)
T = e1t1 + e2t2 +e3t3 |
(13.11) |
Это получается следующим образом: пусть матрица – столбец ортов и матрица – строка имеют вид
e |
|
|
|
|
|
|
1 |
|
|
E = (e1 |
, e2 |
, e3 ) |
|
E = e2 |
|
или |
(14.11) |
|||
|
|
|
|
|
|
|
e3 |
|
|
|
|
|
|
а векторы тензора записаны в форме |
|
|
|
|
|
|
t1 = e1t11 + e2t12 +e3t13 |
|
|
|
|||
t2 = e1t21 +e2t22 +e3t23 |
|
|
(15.11) |
|||
t3 = e1t31 + e2t32 +e3t33 |
|
|
|
|||
потому что произведение тензора на столбец ортов справа получается в виде
t |
|
t |
|
t |
|
|
e |
|
|
e t |
+ e |
t |
|
+e |
|
t |
|
|
t |
|
|
|
|||
11 |
12 |
13 |
|
1 |
|
|
1 11 |
|
2 12 |
|
3 13 |
|
1 |
|
|
||||||||||
T E = t21 |
t22 |
t23 |
|
e2 |
|
= e1t21 +e2t22 + e3t23 |
|
= t2 |
|
(15.11) |
|||||||||||||||
t |
31 |
t |
32 |
t |
33 |
|
e |
3 |
|
e t |
+ e |
2 |
t |
32 |
+e |
3 |
t |
33 |
|
t |
3 |
|
|
||
|
|
|
|
|
|
|
1 31 |
|
|
|
|
|
|
|
|
|
|||||||||
Если умножить матрицу-столбец (14.11) слева на E , получим исходный тензор
e1 T = E T E = e2e3
|
|
e1t11 +e2t12 +e3t13 |
|
t11 |
||||||||||
|
|
e t |
+e |
2 |
t |
22 |
+ e |
3 |
t |
23 |
= |
t |
21 |
|
|
|
|
1 21 |
|
|
|
|
|
|
|||||
|
|
e t |
+e |
2 |
t |
32 |
+e |
3 |
t |
33 |
|
t |
31 |
|
|
|
|
1 31 |
|
|
|
|
|
|
|||||
t12 t22 t32
t13
t23 (16.11)
t33
Умножение тензора Т скалярно на вектор а даёт выражение нового вектора a' a' = T a = e1 (t1 a) + e2 (t2 a) + e3 (t3 a) =
= e1 (t11a1 + t12a2 + t13a3 ) +e2 (t21a1 + t22a2 + t23a3 ) + |
(17.11) |
+ e3 (t31a1 + t32a2 +t33a3 )
Произведение тензора Т на вектор а с последующим свёртыванием
Определение 4.11 Скалярным произведением тензора Т на вектор а называется вектор a' , составляющие которого линейным образом выражаются через составляющие вектора а, причём коэффициентами являются компоненты тензора Т.
Замечание 6.11 Вектор a' = T a называется линейной векторной функцией вектора а.
Рассмотрим произведение, в котором производится свёртывание по первому индексу тензора Τik Ai . Это получается при умножении сопряженного (транспонированного)
тензора
51

t11 t21 t31 Tc = 
 Tik
Tik 
 = t12 t22 t32 t13 t23 t33
= t12 t22 t32 t13 t23 t33
на вектор справа
t |
a +t |
21 |
a |
2 |
+ t |
31 |
a |
3 |
|
t |
t |
21 |
|||
11 1 |
|
|
|
|
|
|
11 |
|
|||||||
Tc a = t12a1 +t22a2 + t32a3 |
|
= t12 |
t22 |
||||||||||||
t |
a +t |
23 |
a |
2 |
+t |
33 |
a |
3 |
|
t |
t |
23 |
|||
13 1 |
|
|
|
|
|
|
13 |
|
|||||||
или исходного тензора на вектор слева
t |
31 |
|
a |
|
|
|
|
1 |
|
= Tik a i |
|
t32 |
|
a2 |
|
||
t33 |
|
|
|
|
|
|
a3 |
|
|
||
|
t |
t |
|
11 |
12 |
a T = (a1 a2 |
a3 ) t21 |
t22 |
|
|
t32 |
|
t31 |
t |
|
|
a t |
+ a |
2 |
t |
21 |
+ a |
3 |
t |
31 |
|
|
13 |
|
|
1 11 |
|
|
|
|
|
|||||
t23 |
|
= a1t12 +a2t22 + a3 t32 |
|
||||||||||
t |
33 |
|
a t |
+ a |
2 |
t |
23 |
+ a |
3 |
t |
33 |
|
|
|
|
|
1 13 |
|
|
|
|
|
|||||
Тогда произведение вектора а на тензора Т получается в виде |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
a' = a T = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) (18.11) |
||
= e |
(t |
a +t |
21 |
a |
2 |
+t |
31 |
a |
3 |
) +e |
2 |
(t |
a +t |
22 |
a |
2 |
+t |
32 |
a |
3 |
) +e |
3 |
(t |
a + t |
23 |
a |
2 |
+t |
33 |
a |
3 |
|
1 |
11 |
1 |
|
|
|
|
12 |
1 |
|
|
|
|
13 |
1 |
|
|
|
|
||||||||||||||
Замечание 7.11 Из получения произведений тензора Т на вектор а видно, что можно использовать исходный и сопряжённый тензор для получения одного и того же выражения, поэтому справедливо равенство
a T = Tc a |
(19.11) |
Свёртывание по второму индексу произведения тензора Т на вектор а
Для этого тензор Т умножается на вектор а справа
t a |
+t a |
2 |
+ t a |
3 |
|
t |
|
|||||||
11 1 |
12 |
|
13 |
|
|
11 |
||||||||
t21a1 +t22a2 + t23a3 |
|
= t21 |
||||||||||||
t |
a |
+t |
32 |
a |
2 |
+ t |
33 |
a |
3 |
|
t |
31 |
||
|
31 1 |
|
|
|
|
|
|
|
|
|||||
t |
t |
|
a |
|
|
12 |
13 |
|
1 |
|
|
t22 |
t23 |
|
a2 |
|
= Tik ak |
t32 |
|
|
|
|
|
t33 |
a3 |
|
|
||
Тогда произведение тензора Т на вектор а справа получается в виде |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
a' = T a = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) (20.11) |
|||||
= e |
(t |
|
a |
+t |
a |
2 |
+t |
|
a |
3 |
) + e |
2 |
(t |
21 |
a +t |
22 |
a |
2 |
+t |
23 |
a |
3 |
) +e |
3 |
(t |
31 |
a |
+ t |
32 |
a |
2 |
+t |
33 |
a |
3 |
|||||
1 |
|
|
11 |
1 |
|
12 |
|
13 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||
Это получается также, если умножить сопряжённый тензор Т с на вектор а слева |
||||||||||||||||||||||||||||||||||||||||
(a a |
|
|
|
) |
t11 |
|
t21 |
t31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
a |
3 |
t |
12 |
|
t |
22 |
t |
32 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
t |
13 |
|
t |
23 |
t |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
= (a1t11 + a2t12 + a3t13 |
a1t21 + a2t22 + a3t23 |
a1t31 + a2t32 + a3t33 ) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
a' = a Tc |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= e1 (t11a1 + t12a2 + t13a3 ) + e2 (t21a1 + t22a2 + t23a3 ) +e3 (t31a1 + t32a2 + t33a3 )
Пример 2.11 Найти произведение aij x j тензора второго ранга aij , матрица которого в некотором базисе равна
|
2 |
0 |
3 |
|
|
|
5 1 2 |
|
, |
||
(aij ) = |
|
||||
|
4 |
5 |
7 |
|
|
|
|
|
|||
и тензора первого ранга xi (вектора), который в том же базисе имеет компоненты
(xi ) = ( 2 1 4 ),.
Решение.
52
a1 j x j = a11x1 + a12 x2 + a13 x3 = 2 2 + 0 1 + 3 4 =16 a2 j x j = a21x1 + a22 x2 + a23 x3 = 5 2 +1 1 + 2 4 =19 a3 j x j = a31x1 + a32 x2 + a33 x3 = 4 2 +5 1 + 7 4 = 41
Ответ: Вектор(16, 19, 41) |
|
Умножение вектора а на тензор Т |
|
a" = a T = (a e1) t1 + (a e2 ) t2 +a e3 t3 |
(21.11) |
Координаты вектора a" получаются в виде |
|
a1" = a1t11 + a2t21 + a3t31 |
|
a"2 = a1t12 + a2t22 + a3t32 |
(22.11) |
a"3 = a1t13 + a2t23 + a3t33 |
|
Геометрическая интерпретация произведения вектора а на тензор Т |
|
Произведение a T так составлено по векторам t1 , t2 t3 , как вектор a |
составлен из |
основных ортов i1, i2 i3 .
Для получения геометрической интерпретации ограничимся случаем двумерного пространства.
a = i1a1 + i2a2
a' = a1 t1 + a2 t2
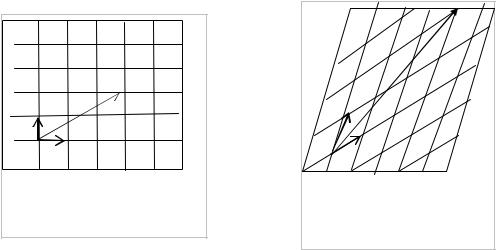
Построим на взаимно перпендикулярных ортах i1 и i2 квадратную решётку из
растяжимых прутьев, соединённых шарнирами, как показано на рисунке 1.11. Теперь растянем стержни и повернём так, чтобы квадраты перешли в параллелограммы, как показано на рис.2.11. Тогда вектор а перейдет в новый вектор a’.
|
а |
i2 |
|
O |
i1 |
Рис.1.11 Вектор а в |
|
|
системе i1, i2 |
Произведение тензоров |
|
a’ |
t2 |
O’ t1 |
Рис.2.11 Вектор а’ в |
системе t1, t2 |
Пусть Aik и Bik - компоненты двух тензоров второго ранга. Их произведение будет иметь компоненты
Ciklm = Aik Blm |
(23.11) |
Числа Ciklm образуют тензор 4 –го ранга. Д о к а з а т е л ь с т в о:
53
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A' |
|
=α |
i'l |
α |
k 'm |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ik |
|
|
|
|
lm |
|
|
|
|
|
|
|
|
|
|
|
(24.11) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
' |
|
=α |
|
α |
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i'l |
k 'm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ik |
|
|
|
|
lm |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
C' |
iklm |
= A' |
|
B' |
= α |
i'n |
α |
k' |
p |
α |
k'r |
α |
|
A |
|
B |
r s |
= α |
i'n |
α |
k' |
p |
α |
k'r |
α |
m's |
C |
n prs |
(25.11) |
|||||||
|
|
|
ik |
|
ik |
|
|
|
|
|
m's |
n p |
|
|
|
|
|
|
|
|
|||||||||||||||||
Определение |
5.11 |
Операция |
образования |
компонент |
|
Ciklm |
|
называется |
внешним |
||||||||||||||||||||||||||||
умножением тензоров Aik и Bik . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Замечание 8. 11 |
Тензорное произведение некоммутативно. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Ciklm = Aik Blm ≠ Clm ik |
= Alm Bik |
|
|
|
|
|
|
|
|
|
|
(26.11) |
||||||||||||||||||
Определение 6.11 Произведением нескольких тензоров называется тензор, компоненты |
|||||||||||||||||||||||||||||||||||||
которого равны |
произведению компонент сомножителей. |
При этом ранг произведения |
|||||||||||||||||||||||||||||||||||
равен сумме рангов сомножителей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Определение 7.11 Внешним произведением тензоров произвольного ранга называется |
|||||||||||||||||||||||||||||||||||||
новый тензор, у которого компоненты образованы умножением каждой компоненты |
|||||||||||||||||||||||||||||||||||||
одного тензора на каждую компоненту второго. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
a) aib j = Tij |
|
b) ai Flk |
= αilk |
|
|
c) DijTlm |
= Φijlm |
|
e) εijkυm =θijkm |
|
|
(27.11) |
|||||||||||||||||||||||||
Замечание 9.11 Как видно из этих примеров, внешние произведения получаются путём |
|||||||||||||||||||||||||||||||||||||
написания умножения тензоров друг за другом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Замечание 10.11 |
|
Внешнее произведение двух векторов образует одну диаду. |
|
||||||||||||||||||||||||||||||||||
|
§ 12. |
Главные значения и главные направления тензора второго ранга. |
|||||||||||||||||||||||||||||||||||
Основные понятия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Рассмотрим произвольный тензор 2-го ранга Τik |
. Если этот тензор умножить на вектор |
|||||||||||||||||||||||||||||||||||
Ak |
и произвести |
|
свёртывание |
по |
|
индексу вектора и одному индексу тензора, то в |
|||||||||||||||||||||||||||||||
результате получим некоторый вектор Bi |
с компонентами |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bi = Τik Ak |
|
|
|
|
|
|
|
|
|
|
|
|
Ak , |
|
(1.12) |
||||||||
|
Тензор Τik , будучи умножен скалярно на некоторый вектор |
преобразует его в |
|||||||||||||||||||||||||||||||||||
новый вектор в том смысле, что из компонент вектора |
Ak |
определённым действием |
|||||||||||||||||||||||||||||||||||
получаются компоненты другого вектора – вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Bi . Вектор Bi |
вообще отличен от Ak |
по величине и |
|
|
|
|
|
|
|
|
|
' |
|
x3 |
p1 |
||||||||||||||||||||||
направлению. Таким образом, |
|
тензор |
|
при |
|
|
|
|
|
|
|
|
x3 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
|||||||||||||||||||||||
умножении на вектор изменяет длину этого |
|
p3 |
n3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
вектора и поворачивает его оси. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Задача заключается в том, чтобы найти для |
|
|
|
|
|
|
|
|
|
|
|
|
x2' |
|||||||||||||||||||||||
данного тензора |
|
Τik такие векторы |
Ak , |
которые |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
бы не поворачивались этим тензором, а только |
|
x1 |
|
|
|
|
|
|
|
|
|
x2 |
|||||||||||||||||||||||||
изменяли длину (рис. 4.12). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|||
|
|
|
|
|
|
|
Τik Ak |
= λAi , |
|
|
|
|
|
(2.12) |
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|||||||||
где λ - скаляр. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.12 |
Главные оси тензора |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напряжений |
pik |
в точке М. На |
|||||||||||
|
Физический |
смысл |
этой |
|
задачи |
виден |
на |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
площадках, перпендикулярным к |
||||||||||||||||||||||||||||||||
некоторых примерах. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
осям |
x' , x' |
, x' |
, касательные |
||||||||||||||
Задача 1.12 Напряжение на площадке с нормалью |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|||||||||||||||||||||||||
n равно |
|
|
|
|
|
pnk |
= pik ni |
|
|
|
|
|
(3.12) |
|
|
|
|
|
|
напряжения равны нулю. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
54 |

причём вообще вектор pn не параллелен орту n , то есть, на каждой площадке есть как
нормальные, так и касательные напряжения.
Интерес представляют такие площадки, на которых есть только нормальные напряжения, а касательные равны нулю. Для этих площадок
pn || n или λn = pn = pi ni
Тогда ориентация этих площадок, которую дают орты n , определится из системы уравнений
λnk = pik ni . |
(4.12) |
Задача 2.12 Если диэлектрические свойства среды определяются тензором Tik , то
возникает вопрос, как следует направить электрическое поле Е, чтобы электрическая индукция D была направлена по вектору напряжённости Е?
Общий вид зависимости D и Е имеет линейный характер
Di = Tik Ek |
(5.12) |
Поставленная задача требует отыскания векторов Ei , удовлетворяющих уравнениям |
|
λ Ei = Tik Ek |
(6.12) |
Определение 1.12 Если существуют для тензора Tik |
векторы Ak , удовлетворяющие |
уравнениям |
|
λ Ai = Tik Ak , |
(7.12) |
то направления, определяемые этими векторами |
Ak , называются главными |
(собственными) направлениями тензора Tik .
Определение 2.12 Оси главных направлений называются главными осями тензора. Определение 3.12 Значения компонент тензора в координатной системе главных осей называются главными значениями.
Определение главных направлений и главных значений тензора Tik
Согласно (7.12) компоненты вектора А, определяющие оси тензора Tik , удовлетворяют системе трёх уравнений:
Tik Ak |
−λ Ai = (Tik − λδik ) Ak = 0 |
(8.12) |
|
или |
|
|
|
(T11 − λ) A1 + |
T12 A2 + |
T13 A3 = 0 |
|
T21 A1 + (T22 − λ) A2 + |
T23 A3 = 0 |
(9.12) |
|
T31 A1 + |
T32 A2 + (T33 − λ) A3 = 0 |
|
|
Эта однородная система служит |
для определения A1 , A2 , A3 . |
При этом, ищется |
|
отличное от нуля, или, нетривиальное решение этой системы. Однородная система уравнений имеет нетривиальное решение только в том случае, когда её определитель равен нулю. Таким образом, для определения главных значений имеется уравнение
(T11 − λ) |
T12 |
T13 |
|
|
|
|
|||
T21 |
(T22 − λ) |
T23 |
= 0 |
(10.12) |
T31 |
T32 |
(T33 − λ) |
|
|
Уравнение (10.12) представляет собой кубическое уравнение относительно λ .
Определение 4.12 Уравнение (10.12) называется характеристическим уравнением
тензора Tik .
55

Замечание 1.12 Корни кубического уравнения (10.12) в общем случае могут быть не все действительными, и тогда из этого уравнения нельзя найти главные направления тензора Tik .
Замечание 2.12 При отнесении тензора к системам обобщённых координат можно использовать его любые компоненты для определения его главных направлений и значений.
Например, если известны ковариантные компоненты тензора Tik , то уравнение, определяющее собственные векторы А , имеет вид:
|
|
|
|
λ A = T |
Ak . |
|
(11.12) |
||
|
|
|
|
i |
ik |
|
|
|
|
Отсюда в силу |
A = g |
ik |
Ak |
получим |
систему линейных |
однородных уравнений |
|||
|
i |
|
|
|
|
|
|
|
|
относительно Ak |
вида |
|
|
|
|
|
) Ak |
|
|
|
|
|
|
(T |
− λ g |
ik |
= 0 . |
(12.12) |
|
|
|
|
|
ik |
|
|
|
|
|
Однако, для того, чтобы привести эту систему |
к виду (9.12), необходимо пользоваться |
|||||||||||||||
смешанными компонентами |
тензора |
|
|
g i |
= δ i |
. Умножив |
предыдущие уравнения |
|||||||||
|
|
|
|
|
|
|
|
.k |
.k |
|
|
|
|
|
|
|
(i =1,2,3) на g il , пронумеровав по i , получим в силу уже известных формул |
||||||||||||||||
Aik = g il g km A , |
A |
= g |
il |
g |
km |
Alm , |
A |
= g |
A l |
= g |
il |
Al |
|
|||
|
|
lm |
ik |
|
|
|
|
ik |
|
kl i |
|
k ' |
|
|||
|
Al k = g kl Ail , |
|
Al k = gil Alk , |
|
|
|
|
|
|
, |
||||||
|
|
|
|
|
|
|
|
|||||||||
Ai |
= g il A , |
Ai |
= g |
|
Ail , |
|
Aik = g il A k |
= g kl Ai |
. |
|
|
|
||||
kl |
|
|
|
|
||||||||||||
k |
lk |
k |
|
|
|
|
|
|
l |
|
l |
|
|
|
|
|
следующие уравнения |
(T i k |
− λ g i k ) Ak = 0 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
(13.12) |
||||||||
Тогда для определения собственных значений тензора получаем характеристическое уравнение вида
(T 1 1 − λ) |
T 1 2 |
T 1 3 |
|
|
T 2 1 |
(T 2 2 − λ) |
T 2 3 |
= 0 |
(14.12) |
T 3 1 |
T 3 2 |
(T 3 3 − λ) |
|
|
Замечание 3.12 Обычно рассматриваются только симметричные тензоры, потому что у них корни характеристических уравнений всегда действительные.
Остановимся на рассмотрении симметричных тензоров второго ранга, отнесённых к прямоугольным декартовым системам координат, так что Ti k = Tk i . В этом случае все
корни λ1 , λ2 , λ3 характеристического уравнения (13.12) вещественные
(действительные).
Действительно, пусть λ - какой-нибудь из корней уравнения (13.12) и пусть ему отвечают в силу системы уравнений (9.12) какие-то величины Ai , вообще комплексные.
Тогда умножив каждое (i =1,2,3) из тождеств
λ Ai = Tik Ak |
(15.12) |
на величины Ai , комплексно сопряжённые с Ai , и просуммировав по i , получим
|
|
|
|
|
|
|
λ Ai |
|
|
= Tik Ak |
|
|
|
|
|
|
(16.12) |
|||||||||
|
|
|
|
Ai |
Ai |
|
|
|||||||||||||||||||
Так как Ti k = Tk i , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
T A |
|
= |
1 |
(T A |
|
+T A |
|
)= |
1 |
(T A |
|
+T |
|
A )= |
1 |
T |
(A |
|
+ |
|
A ). |
|||||
A |
A |
A |
A |
A |
A |
A |
||||||||||||||||||||
2 |
2 |
|
||||||||||||||||||||||||
ik k i |
ik k i ik k i |
ik k i k i k i |
2 ik |
k i k i |
||||||||||||||||||||||
56

Отсюда видно, что сумма Tik Ak Ai вещественна, так как все Ti k вещественны и выражение в скобках вещественно. Вспомним, что произведение комплексного числа на сопряжённое
z z = (x + iy) (x −iy) = x2 + y2 |
равно сумме квадратов вещественных чисел. Поскольку |
|||||||||||||||||||||||
A |
|
= |
|
A |
|
2 + |
|
A |
|
2 + |
|
A |
|
2 - тоже вещественная величина, то из (15.12) следует, что корень |
||||||||||
A |
|
|
|
|
|
|
||||||||||||||||||
i |
i |
|
|
1 |
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||
λ вещественная величина. При этом, конечно, все компоненты Ak |
тоже вещественны (это |
|||||||||||||||||||||||
следует из λ Ai = Tik Ak ). |
|
|
|
|
|
|
|
|||||||||||||||||
Итак, λ1 , λ2 , λ3 - вещественные числа. |
|
|
|
|
||||||||||||||||||||
|
Заметим, |
что если |
|
Ti k - ковариантные компоненты тензора, то, |
исходя из равенства |
|||||||||||||||||||
λ A = T |
|
Ak , |
|
|
умножая |
|
его на |
|
|
, суммируя по i и используя |
T |
|
= T |
, аналогично |
||||||||||
|
|
|
|
|
A |
|
||||||||||||||||||
|
i |
|
|
ik |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
i k |
k i |
|
|||
предыдущему получим вещественность характеристического уравнения (13.12).
Главные значения и главные направления симметричных тензоров второго ранга
В дальнейшем будут рассмотрены только симметричные тензоры с действительными компонентами. Это несколько проще в математическом отношении, так как тензоры, важные для механики сплошной среды, обычно симметричны, то жертвуя немногим, целесообразно принять такое ограничение.
Для каждого симметричного тензора Ti j , заданного в некоторой точке пространства, и для каждого направления в этой точке (характеризуемого единичным вектором ni ) существует вектор, определяемый внутренним произведением (см. определение 6.11)
υi = Ti j n j |
(17.12) |
Здесь Ti j можно рассматривать как линейный векторный оператор, который ставит в
соответствие направлению ni вектор υi . Если направление таково, что |
вектор υi |
|
параллелен ni , |
то указанное внутреннее произведение выражается |
скаляром, |
умноженным на ni . В этом случае (так как υi = λ ni ) получается |
|
|
|
Ti j n j = λ ni |
(18.12) |
и направление ni |
называется главным направлением или главной осью тензора Ti j . С |
|
помощью тождества ni = δi j n j соотношению (18.12) можно придать форму |
|
|
|
(Ti j − λδi j )n j = 0, |
(19.12) |
которое представляет систему трёх уравнений для четырёх неизвестных ni и λ ,
соответствующих каждому главному направлению. В развёрнутой записи система, которую следует решить, имеет вид
(T11 − λ) n1 + T12 n2 + T13 n3 = 0 |
|
T21 n1 + (T22 − λ) n2 + T23 n3 = 0 |
(20.12) |
T31 n1 + T32 n2 + (T33 − λ) n3 = 0
Это однородная система уравнений, поэтому при любом λ существует тривиальное решение ni = 0 , но наша цель состоит в том, чтобы получить нетривиальное решение, то есть отличное от нуля. Кроме того, не теряя общности, можно ограничится только
решениями, для которых |
n |
n |
i |
=1 |
(это значит, что n2 |
+ n2 |
+ n2 |
=1, что справедливо, так |
|
i |
|
|
1 |
2 |
3 |
|
|
как с самого начала вектор |
|
ni предполагался единичным). |
Для того, чтобы система |
|||||
(19.12) или, что то же самое (20.12), имела нетривиальное решение, определитель из коэффициентов должен быть равен нулю, что можно записать так:
57
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ti j − λδi |
j |
= 0 . |
|
|
|
(21.12) |
|||||||
В развёрнутом виде это кубическое уравнение относительно λ : |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ3 − I |
T |
λ2 |
+ II |
T |
λ − III |
= 0 , |
(22.12) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|||
которое |
является |
|
характеристическим |
|
уравнением |
тензора |
Ti j , а его скалярные |
|||||||||||||||||||||||||||||
коэффициенты соответственно равны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
IT =Tii |
=T11 +T22 +T33 (= λ1 +λ2 +λ3 ) = inv |
|
|
|
|
|
|
(23.12) |
||||||||||||||||||||||||||||
II = |
1 |
(T T |
jj |
|
|
−T |
T |
j i |
) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
T |
2 |
|
ii |
|
|
|
i j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(24.12) |
|
= |
|
T22 |
|
|
T23 |
|
+ |
|
T11 |
T21 |
|
+ |
|
T11 |
T31 |
|
(= λ λ |
2 |
+ λ λ |
3 |
+ λ |
2 |
λ ) = inv |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
T32 |
|
|
T33 |
|
|
|
|
|
T12 |
T22 |
|
|
|
T13 |
T33 |
|
1 |
|
|
1 |
|
3 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T11 T12 |
|
T13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
IIIT =detTi j |
= |
T21 |
|
T22 |
|
T23 |
(=λ1λ2λ3 ) =inv |
|
|
|
|
|
|
(25.12) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T31 |
|
T32 |
|
T33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
называются соответственно первым, вторым и третьим инвариантами тензора Ti j . Три корня кубического уравнения (20.12), обозначенные λ1 , λ2 , λ3 , называются главными значениями тензора Ti j . У симметричного тензора с действительными компонентами
главные значения действительны; если все они различны, то три главных направления взаимно ортогональны. В главных осях таблица из компонент тензора приводится к диагональной форме
|
λ |
0 |
0 |
|
|
|
1 |
λ2 |
|
|
|
T = |
0 |
0 |
|
(26.12) |
|
|
0 |
0 |
|
|
|
|
λ3 |
|
|||
Замечание 4.12 Если λ1 = λ2 , то диагональный вид тензора не зависит от выбора осей, соответствующих λ1 и λ2 , и нужно установить только главную ось, соответствующую
λ3 .
Замечание 5.12 Если все главные значения равны, то любое направление является
главным.
Если главные значения упорядочены, то их |
принято обозначать λI , λII , λIII и |
||||||||||||||||||
располагать в порядке убывания: λI |
> λII |
> λIII . |
|
|
|
|
|
|
|
||||||||||
Преобразование системы Ox x |
2 |
x |
3 |
к системе главных осей Ox* x* x* |
даётся элементами |
||||||||||||||
таблицы |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x1 |
|
|
|
|
|
|
x2 |
|
x3 |
|
|
|
|
|
|||
|
x* |
a |
|
= n |
(1) |
|
a |
|
= n(1) |
a |
|
= n(1) |
|
|
|
|
|||
|
1 |
11 |
|
|
1 |
|
|
12 |
2 |
13 |
3 |
|
|
|
|
||||
|
x* |
a |
21 |
= n(2) |
|
a |
22 |
= n(2) |
a |
23 |
= n(2) |
|
|
|
|
||||
|
2 |
|
|
|
|
1 |
|
|
|
2 |
|
3 |
|
|
|
|
|||
|
x* |
a |
31 |
= n(3) |
|
a |
32 |
= n(3) |
a |
33 |
= n(3) |
|
|
|
|
||||
|
3 |
|
|
|
|
1 |
|
|
|
2 |
|
3 |
|
|
|
|
|||
где ni( j) - направляющие косинусы j - того главного направления.
Пример 1.12 Найти главные направления и главные значения декартова тензора Т второго ранга, который представлен матрицей
58
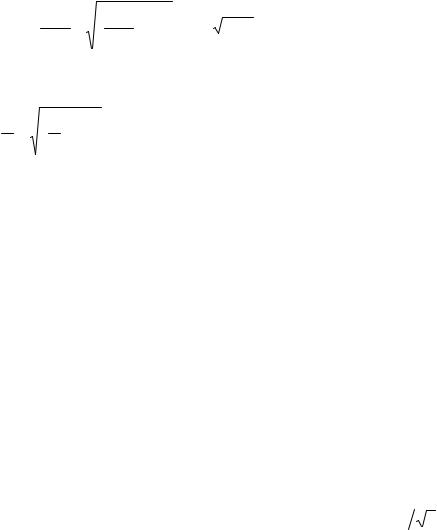
|
|
3 |
−1 |
0 |
||
[T |
]= −1 |
3 |
0 |
|||
ik |
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
|
|
|
|
|
|||
Решение. Для определения главных значений необходимо решить уравнение
3 − λ |
−1 |
0 |
|
|
|
|
|
|
|
−1 |
3 − λ |
0 |
|
= (1 − λ)[(3 − λ) |
2 |
−1] |
= 0 |
|
|
|
||||||
|
0 |
0 |
1 − |
|
|
|
|
|
|
λ |
|
|
|
|
|||
Это кубическое уравнение
λ3 −7λ2 +14λ −8 = 0
Но совершенно очевидно, что один корень известен λ1 =1. Поделив кубическое уравнение на λ −1, получим
λ2 −6λ +8 = 0
Это квадратное уравнение имеет два корня
λ2,3 = − |
(−6) |
± |
(−6) 2 |
−8 = 3 ± 9 −8 = 3 ±1 |
|||
|
|
|
|
2 |
|
2 |
|
λ2 |
= 2, |
|
λ3 = 4 |
|
|
||
Замечание 6.12. Здесь использовано квадратное уравнение вида x2 + px + q = 0 , решение |
|||||||
которого равно x1,2 = − |
p |
± |
|
p |
2 |
|
|
2 |
|
|
− q |
|
|||
|
|
|
2 |
|
|
|
|
Таким образом, найдены все три главные значения λ1 =1 λ2 = 2, |
λ3 = 4 |
|
|
|
|
|||||||||||||||
Определение главных направлений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
а) Пусть ni1 |
- |
компоненты единичного вектора |
главного |
направления , |
||||||||||||||||
соответствующего λ1 =1. Тогда два первых уравнения системы |
|
|
|
|
|
|
||||||||||||||
|
|
(3 − λ) n1 |
−n1 |
+ 0 n31 = |
0 |
|
2 n1 |
−n1 |
+ 0 n31 |
= 0 |
|
|
|
|
|
|||||
|
|
|
|
1 |
2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
−n11 + (3 − λ) n12 + 0 n31 |
= 0 |
−n11 + 2 n12 + 0 n31 = 0 |
|
|
|
|
||||||||||||
|
|
0 n1 + 0 n1 + (1 − λ) n1 |
= 0 |
0 n1 + 0 n1 + 0 n1 = 0 |
|
|
|
|
||||||||||||
|
|
|
1 |
|
2 |
3 |
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
дают 2n1 |
− n1 |
= 0, |
− n1 + 2n1 = 0, |
откуда n1 |
= n1 |
= 0, |
а |
из |
условия |
n |
n |
i |
=1 получим |
|||||||
|
1 |
2 |
|
|
1 |
2 |
|
1 |
|
2 |
|
|
|
|
|
|
i |
|
|
|
n31 = ±1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Для λ2 |
= 2, |
система уравнений (4) имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
(3 − λ) n2 |
−n2 |
+ 0 n32 = 0 |
|
n2 |
−n2 |
+ 0 n32 |
= 0 |
|
|
|
|
|
||||||
|
|
|
|
1 |
2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
−n12 + (3 − λ) n22 + 0 n32 |
= 0 −n12 +n22 + 0 n32 = 0 |
|
|
|
|
|||||||||||||
|
|
0 n2 + 0 n2 + (1 − λ) n2 |
= 0 |
0 n2 |
+ 0 n2 −n2 = 0 |
|
|
|
|
|||||||||||
|
|
|
1 |
|
2 |
3 |
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
даёт n2 |
− n2 = |
0, − n2 |
+ n2 |
= 0, и − n2 |
= 0. Таким образом, |
n2 |
= 0, |
а n2 |
= n2 |
= ±1 2 , так |
||||||||||
1 |
|
2 |
|
1 |
2 |
|
3 |
|
|
|
|
|
|
3 |
|
1 |
|
2 |
|
|
как ni ni |
=1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) Для λ3 |
= 4 из системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
(3 − λ) n3 |
−n3 |
+ 0 n33 = |
0 |
|
−n3 |
−n3 + 0 n33 = 0 |
|
|
|
|
||||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
−n13 + (3 − λ) n32 + 0 n33 |
= 0 −n13 −n32 + 0 n33 = 0 |
|
|
|
|
|||||||||||||
|
|
0 n3 + 0 n3 + (1 − λ) n3 |
= 0 |
0 n3 |
+ 0 n3 −3n3 |
= 0 |
|
|
|
|
||||||||||
|
|
|
1 |
|
2 |
3 |
|
|
|
|
1 |
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
59
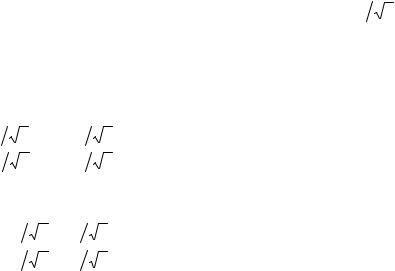
получаем −n3 |
−n3 |
= 0 , |
−n3 |
−n3 |
= 0 |
3 n3 |
= 0 . Таким образом, n3 |
= 0, а n3 |
= n3 |
= m1 2 . |
1 |
2 |
|
1 |
2 |
|
3 |
3 |
1 |
2 |
|
Ориентация главных осей xi' относительно исходной системы xi определяются направляющими косинусами, которые даны в следующей таблице
|
x1 |
|
x2 |
|
x3 |
x1' |
0 |
|
0 |
|
±1 |
x2' |
±1 |
2 |
±1 |
2 |
0 |
x3' |
m1 |
2 |
±1 |
2 |
0 |
Ответ Из таблицы видно, что матрица преобразования такова:
0 |
|
0 |
|
±1 |
A = ±1 |
2 |
±1 |
2 |
0 |
±1 |
2 |
±1 |
2 |
0 |
Степени тензора второго ранга. Соотношения Гамильтона –Кэли
Непосредственным матричным умножением квадрат тензора Ti j получается как внутреннее произведение Ti k Tk j , куб – как произведение Ti k Tk mTm j и т.д. Таким образом,
если Ti j представлен в диагональной форме (26.12), то |
n -я степень этого тензора (и |
||||||||||
соответствующей матрицы) даётся формулой |
|
|
|
|
|
|
|||||
|
|
λn |
0 |
0 |
|
|
λn |
0 |
0 |
|
|
(T)n = |
|
1 |
λn |
|
|
|
1 |
|
|
|
|
|
0 |
0 |
|
или T n = |
0 |
λn |
0 |
|
(27.12) |
||
|
|
|
2 |
n |
|
|
|
2 |
|
|
|
|
|
0 0 λ |
|
|
|
|
n |
|
|
||
|
|
3 |
|
|
0 0 λ3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 7.12 Сравнение (26.12) и (27.12) |
|
показывает, что тензор Ti j |
и все его целые |
||||||||
степени имеют одни и те же главные оси.
Все главные значения удовлетворяют уравнению (22.12), а матрица T n имеет диагональный вид (27.12), поэтому сам тензор Т будет удовлетворять уравнению (22.12). Таким образом,
T 3 − I |
T |
T 2 + II |
T |
T − III |
T |
E = 0 |
(28.12) |
|
|
|
|
|
где Е – единичная матрица. и
Определение 5.12 Соотношение (28.12) называется соотношением Гамильтона – Кэли.
Если умножить каждый член соотношения (28.12) на Т по правилу перемножения матриц, то получается равенство
T |
4 = I |
T |
T 3 |
− II |
T |
T |
2 + III |
|
T |
|
|
|
(29.12) |
||||
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|||
Подставляя T 3 из (28.12), получают |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T 4 = (I2 |
− II |
T |
)T 2 |
+ (III |
− I |
T |
II |
T |
)T + I |
III |
T |
E |
(30.12) |
||||
T |
|
|
|
|
|
T |
|
|
|
T |
|
|
|||||
Замечание 8.12 Продолжая эту процедуру, можно получить все целые положительные степени Т в виде линейных комбинаций Т2, Т и Е.
§ 13. Ковариантное дифференцирование тензоров
Ковариантный дифференциал тензора
Рассмотрим выражение дифференциала вектора а через дифференциалы его
компонент. В декартовой системе координат имеем |
|
da = d (al il ) = il dal . |
(1.13) |
60
