Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Tensor-Gotman

.pdf

Скачиваний:

Добавлен:

09.02.2015

Размер:

1.52 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1311 12 13 > Следующая >>>

pik = −pδik + 2μυik

(24.16)

, а в случае жидкости, находящейся в покое, и в случае идеальной жидкости имеем:

pik = −pδik .

Подставляя различные выражения для pik в уравнение (21.16), получим уравнения движения.

Уравнение движения идеальной жидкости (уравнение Эйлера)

ρ	∂υi		+ ρυk	∂υi	= ρ fi −	∂ p	,
ρ	∂t		+ ρυk		= ρ fi −		,
	∂t			∂ xk		∂xk
в обобщённых координатах
ρ	∂υi		+ ρυkυ i		= ρ f i + p ik			(25.16)
	∂ t			;k		;k
или в векторной записи
ρ	∂v	+ ρ(v )v = ρ f - p ;						(26.16)
ρ	∂t	+ ρ(v )v = ρ f - p ;						(26.16)
	∂t

Уравнение движения вязкой несжимаемой жидкости уравнение Навье – Стокса) при

μ = const

ρ∂υi

+ ρυk

∂υi

= ρ fi −

∂p

+ μ

∂2υi

(27.16)

∂ xk

∂xk

∂ xk ∂ xk

∂t

или в векторной записи

∂v

+ ρ(v )v = ρ f

- p + μ v ,

(28.16)

∂t

Здесь учтено, что divv =

∂υk

= 0 .

∂ xk

в) вязкой сжимаемой жидкости (при μ = const ) –

ρ∂υi

+ ρυk

∂υi

= ρ fi −

∂p

+ μ

∂2υi

∂

∂υk

(29.16)

∂ xk

∂ xk ∂ xk

∂xi ∂ xk

∂t

∂xk

или в векторной форме

∂v

+ ρ(v )v = ρ f - p + μ v +

μ div v

(30.16)

∂t

В случае обобщённых координат уравнение движения должно быть сформулировано относительно компонент векторов.

Пусть поле скоростей есть функция времени t и обобщённых координат x1, x2 , x3 . И

скорость v = v (x1, x2 , x3 ) . Тогда

приращение

скорости

частицы жидкости при

перемещении из точки xi в точку xi

= xi + d xi равно

∂v

d v = d vloc + d vconv ,

∂v

где

d vloc =

- локальная часть

изменения

скорости,

d vconv =

d xk -

∂t

∂ xk

конвективная часть изменения скорости, то есть, ускорение

a =

d v

∂v +

∂v

υk ,

(31.16)

d t

∂t

∂xk

101

или в индексной записи

∂

υ i (x,t)

+υk (x,t)

∂υ i (x,t)

∂t

∂ x k

где υk =

d xk

- контравариантные компоненты скорости.

Отсюда, учитывая

определение ковариантной производной

(

∂A

ei = Ai

), получим

∂xk

контравариантные компоненты ускорений

∂v

∂υ

∂v

d v

+υ

(32.16)

∂ t

∂xk

∂ t

∂xk

d t

Таким образом, в случае обобщённых координат вместо (21.16) получим
ρ	∂υi	+ ρυkυ i	= ρ f i + p ik	(33.16)
	∂ t	;k	;k

где p ;ikk - свёртка ковариантной производной тензора напряжений. В случае вязкой жидкости имеем

p ik

= −pg ik + 2μυ ik

−

μ g ik υ l

(34.16)

где компоненты тензора скоростей деформаций имеют выражение

= g

k m

υlm = g

k m 1

(υl;m +υm;l )

(35.16)

При этом υl

- дивергенция вектора скорости.

Выражение p ik

- дивергенция вектора напряжений.

Учитывая, что ковариантная производная от метрического тензора

gik

равна

нулю, получим

p;ikk

= −pik g ik + 2μυ;ikk −

μg ik (υ;ll );k

(36.16)

Но

[(υl;m )

+ (υm;l )

g k m (υ;lm )

g il (υk )

υik = g il

g k m

] =

(37.16).

Предполагая

∂2υi

, получим

(υk )

(υk

)

Теперь

подставляя

p ik

∂xk ∂xl

∂xl ∂xk

(34.16), можно записать уравнение Навье – Стокса в обобщённых координатах в виде

ρ∂υ i

+ ρυ k υ;ik

= ρ f,i − g ik

∂ p

μ g ik

∂

(υ;ll )+ μg k m (υ;im )

(38.16)

∂xk

∂t

Или, переходя к ковариантным компонентам:

∂υ i

+ ρ υ k υi;k

= ρ f, i −

∂ p

∂

(υ;ll )+ μg k m (υi;m )

(39.16)

∂t

∂xi

Здесь выражение g k m (υ

)

представляет собой ковариантные компоненты вектора

i;m ;k

v .

102

Замечание 1.16 Пользуясь формулами (38.16) и (39.16) и вводя «физические» компоненты векторов, всегда можно получить уравнение Навье-Стокса в любой конкретной системе криволинейных координат.

Закон Архимеда

Сила, действующая со стороны жидкости на погруженное в неё тело с поверхностью S , равна

R = ∫∫pn dS = ∫∫pk nk dS .		(40.16)
S	S
Отсюда	= ∫∫pik nk dS
Ri	= ∫∫pik nk dS	(41.16)
Если жидкость покоится ( v = 0 ), то	S
Если жидкость покоится ( v = 0 ), то
pik = −pδik		(42.16)
ρ = ρ f = ρ g	(массовые силы равны силам тяжести)	(43.16)
Тогда	= −∫∫p ni dS,
Ri	= −∫∫p ni dS,	(44.16)
или	S
или
R = −∫∫p n dS .
	S
Используя теорему Остроградского – Гаусса, получим
R = −∫∫pn dS = −∫∫∫ p dV		(45.16)
S	V

Подставляя p из уравнения равновесия (43.16), получим

R = −∫∫∫ρ g dV = −g∫∫∫ρ dV = −g m = −G .		(46.16)
V	V

Таким образом, сила, действующая со стороны жидкости на погруженное в неё тело, по величине равна G - весу жидкости в объёме тела – и направлена в обратную сторону.

Теорема импульса в гидродинамике

Эта теорема занимает важное место в аэрогидромеханике, особенно в экспериментальной. Эта теорема позволяет определить силу, действующую на выделенный объём жидкости, зная только её скорость (и плотность в случае сжимаемой жидкости) на поверхности этого объёма, а также силу, действующую на помещённое в движущуюся жидкость тело, по напряжениям и скорости (и плотности) жидкости на определённой поверхности (так называемой «контрольной» поверхности).

Количество движения жидкости, находящейся в момент времени в некоторой фиксированной пространственной области V , равно

∫∫∫ρ v dV	(47.16)
V
С течением времени это количество движения меняется, так как через V	проходят
различные массы жидкости. Скорость изменения его равна

103

∂

∫∫∫ρ v dV .

(48.16)

∂t

Поскольку область V является фиксированной, то

∂

∫∫∫ρ v dV = ∫∫∫

∂

(ρ v)dV

(49.16)

∂t

Переходя к компонентам, получим

∂

∂ρ

∂υ

∂t ∫∫∫

∫∫∫∂t

(ρυi )dV =

∫∫∫

∂t

ρυi dV =

υi

+ ρ

(50.16)

∂ρ

Будем считать, что

массовые

силы отсутствуют ( f

= 0 ).

Тогда, определяя

из

∂t

уравнения неразрывности

∂pik

∂υi

+ ρυk

∂υi

= ρ fi +

(51.16)

∂t

∂xk

получим

∂xk

∂

∂υi

∂pik

∫∫∫ρυi dV = ∫∫∫ −

υi

(ρυk )−

ρυk

dV =

∂t

∂ xk

(52.16)

∫∫∫∂ xk

(ρυ υ

)dV

= −

∂

− p

i k

Преобразуя интеграл, стоящий в правой части, по формуле Остроградского – Гаусса

∂

∫∫∫ρυi dV = −∫∫(ρυiυk − pik )nk dS = −∫∫Πik nk dS

(53.16)

∂t

где

Πik

= ρυiυk − pik

(54.16)

Слева в уравнении (53.16) стоит скорость изменения i -той компоненты количества движения жидкости в рассматриваемой ограниченной области. Эта скорость определяется той же i -той компонентой потока тензора Πik через замкнутую поверхность S ,

ограничивающую область (V ) . Таким образом, величина Πik nk dS равна i -той

компоненте того количества движения, которое в единицу времени уносится через элемент поверхности dS , протекающей через V жидкостью. Тогда, очевидно, что величина Πik есть i -тая компонента количества движения, уносимая в единицу времени

через единичную площадь поверхности S , перпендикулярную k - той оси.

Определение 1.16. Тензор Πik называется тензором плотности потока импульса.

Весь поток количества движения через поверхность равен потоку тензора Πik через

неё, то есть.
∫∫Πik nk dS	(55.16)
S	∫∫ρv n dS .
Следует отличать поток импульса от потока вектора ρv , который равен	∫∫ρv n dS .
	S

Поток вектора ρv (количество движения единицы объёма жидкости) по величине равен массе жидкости, протекающей в единицу времени через единичную площадку

104

поверхности S , расположенную	перпендикулярно к скорости. Поэтому				вектор ρv
называют плотностью потока жидкости.
		∂
			= 0	, то из (53.16) получим

Если движение жидкости стационарно		∂ t
		∂ t
∫∫Πik nk dS =∫∫(ρυiυk − pik )nk dS = 0					(56.16)
S	S

Это уравнение выражает теорему импульсов, которую можно сформулировать так:

При стационарном движении жидкости и равенстве нулю массовых сил поток тензора Πik = ρυiυk − pik через любую взятую в жидкости замкнутую поверхность

равен нулю.

Теорема импульсов позволяет непосредственно выразить силу, действующую на выделенный объём жидкости, через скорость и плотность жидкости на поверхности этого объёма (рис. 2.16)..

Действительно, поскольку массовые силы отсутствуют, то

∫∫pik nk dS

(57.16)

даёт i -тую компоненту главного вектора всех сил, действующих на выделенный объём жидкости. Обозначим её через Fi . Таким образом, из (55.16) имеем:

Fi = −∫∫ρυiυk nk dS	(58.16)
S

или в векторной форме

Рис. 2.16 К теореме

импульсов

F = ∫∫ρ v (v n)dS		(59.16)
S
	∂
Пусть в стационарном потоке жидкости		= 0	при

	∂ t
	∂ t

отсутствии массовых сил ( f = 0 ). Помещено твёрдое тело с поверхностью So , произвольную, фиксированную, но так,

чтобы она полностью охватывала твёрдое тело. Применим к объёму жидкости между поверхностью твёрдого тела S и центральной поверхностью So теорему импульсов (50.16) .

Получим

∫∫pik nk dS + ∫∫pik nk dSo −∫∫ρυiυk nk dS − ∫∫ρυiυk nk dSo = 0 .

Первый интеграл даёт выражение для компоненты силы, действующей со стороны тела на рассматриваемы объём жидкости, взятый со знаком минус, он даёт компоненту Ri силы,

действующей со стороны жидкости на тело, то есть

Ri =−∫∫pik nk dS

(60.16)

Третий интеграл равен нулю в силу отсутствия протекания жидкости через поверхность твёрдого тела ( v n =υk nk = 0 на поверхности тела S ).

Следовательно,

105

Ri =∫∫(pik − ρυiυk )nk dSo

(61.16)

Итак, чтобы определить силу, действующую на твёрдое тело в стационарном потоке жидкости, достаточно на некоторой поверхности So , которая может быть удобной для

эксперимента, измерить направление поверхностных сил, скорость и плотность жидкости. Особенно простую формулировку приобретает теорема импульсов, если можно

пренебречь силами вязкости. В этом случае, как уже отмечалось,
Ri =−∫∫(p ni + ρυiυk nk )nk dSo	(62.16)
So
или в векторной записи
R =−∫∫[ p n + ρ v (v n)]dSo	(63.16)
So

Таким образом, в этом случае достаточно на контрольной поверхности произвести замеры давления и вектора скорости жидкости, чтобы получить силу, действующую на твёрдое тело. Этот приём часто используют в аэродинамических экспериментах.

106

ПРИЛОЖЕНИЕ 1. Произведения векторов

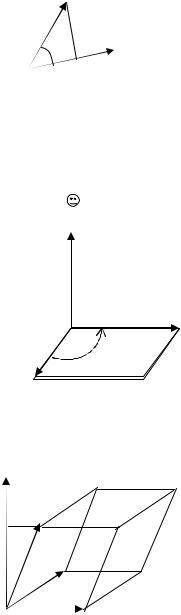
Скалярное произведение двух векторов

Определение 1. Скалярным произведением двух векторов a и b называется произведение их модулей на косинус угла между ними.

a b =

cosα

(1)

прab

(2)

О пр a b

a b =

прba

(3)

Рис. 1 К скалярному

произведению векторов.

Определение 2. Скалярным произведением двух векторов a и b называется произведение модуля одного вектора на проекцию на него другого вектора.

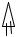c = a × b

Рис. 2. К определению векторного произведение

a × b

h c b

O a

Рис. 3 К смешанному произведению

Векторное произведение двух векторов

Определение 3. Векторным произведением двух векторов a и b называется вектор c , отвечающий следующим трём условиям:

1) модуль вектора c численно равен площади

bпараллелограмма, построенного на векторах a и b ,

2)вектор c направлен перпендикулярно плоскости

векторов a и b ,

3) вектор c направлен в такую сторону, что если смотреть с конца вектора c , то кратчайший путь от вектора a к вектору b происходит против часовой стрелки.

Векторно – скалярное (смешанное) произведение трёх векторов

Определение 4. Смешанным произведением называется векторно – скалярное произведение трёх векторов a , b и c Теорема о смешанном произведении: Смешанное

произведение трёх векторов a , b и c численно равно объёму параллелепипеда, построенного на векторах – сомножителях, взятому со знаком плюс, если тройка векторов правая, и со знаком минус, если– левая.

a ×b c = ±V

(4)

Замечание 1 Если векторы заданы своими координатами в декартовой системе,

a =axi + ay j + azk,
b =bxi +by j + bzk,	(5)
c = cxi + cy j + czk.

то смешанное произведение равно определителю, составленному из координат этих векторов.

107

ax a y az

a ×b c = ± bx	by bz	(6)
cx	cy cz

Векторно – векторное произведение a × (b × c)

b × c	π	c
	2
		b

a×(b ×c)

Рис. 4 К векторно – векторному произведению

Векторно-векторное произведение трёх векторов равно

a × (b × c) = b(a c) −c(a b)	(7)
где три вектора a, b и c даны в декартовой	системе

координат в виде (5)

Из рис. 4 видно, что векторновекторное произведение лежит в одной плоскости с векторами b и c и,

одновременно, перпендикулярно вектору a . Замечание 2. Так как геометрическое доказательство очень громоздко и сложно, просто сравним левую и правую часть равенства (7)

108

ПРИЛОЖЕНИЕ 2 Таблица 1 Выражение элементов полей через коэффициенты Ламэ

№

Величина

Выражение в декартовой

Выражение в ортогональной

системе координат

криволинейной системе

координат

Коэффициенты

Hi =

(∂ x1

∂ξi )2 + (∂ x2

∂ξi )2 + (∂ x3

∂ξi )2

Ламэ

Радиус – вектор

r = x1e1 + x2e2 + x3e3

r = r (ξ1 ,ξ2 ,ξ3 )

точки М

Дифференциал

d r

= d s

d r =

∂si

ξk ei

= Hi d ξiei

радиуса - вектора

∂ξk

Дифференциал

ds =

(dx1 )2 + (dx 2 )2 + (dx3 )2 ,

длины дуги при

∂ x1

x1 = x1 (ξ1 ,ξ2 ,ξ3 ),

dx1 =

dξ1 +

dξ2

dξ3

∂ ξ1

∂ ξ2

∂ ξ3

d si

= Hi d ξi

x2 = x2 (ξ1 ,ξ2 ,ξ3 ),

∂ x2

dx 2 =

dξ1

dξ2 +

dξ3

= x

(ξ

,ξ

∂ ξ

dx3 =

∂ x3

dξ1

∂ x3

dξ2

∂ x3

dξ3

∂ ξ1

∂ ξ2

∂ ξ3

Дифференциал

dσ1 = ds2 ds3

dσ1 = H 2 H3d ξ2 d ξ3 ,

площади

dσ2 = ds1 ds3

dσ2 = H3 H1d ξ3d ξ1 ,

dσ3 = ds1 ds2

dσ3 = H1H 2 d ξ1d ξ2

Дифференциал

dV = ds1 ds2 ds3

dV = H1H 2 H3dξ1dξ2dξ3 .

объёма

Градиент

gradϕ(ξ

,ξ

) =

∂ϕ

скалярного поля

∂ϕ

∂ξk

gradϕ = ϕ

ϕ = i ∂ x + j

∂ y

∂ z

∂ϕ

. .

∂ξ

Дивергенция

div a = a =

∂ax

∂a y

∂az

div a =

векторного поля

+ ∂ z

H1H 2 H 3

∂ x

∂ y

div a = a

∂(a H

)

∂(a

)

∂(a

)

∂ξ1

∂ξ2

∂ξ3

Ротор векторного

(rot a )

поля

∂(a 3 H 3 )

∂(a 2 H 2 )

∂

= ( H 2

3 )

−1

×a =

−

∂ ξ

rot a = ×a

∂ x

∂ y

∂ z

(rot a )2 =

a y

∂(a1 H 1 )

∂(a 3 H 3 )

−1

= ( H 3

H 1 )

−

∂ ξ 3

∂ ξ1

(rot a )3

∂(a 2 H 2 )

∂(a1 H 1 )

= ( H 1 H 2 )

−1

−

∂ ξ1

∂ ξ 2

109

Таблица 2 Элементы векторной алгебры в тензорных выражениях

Скалярное произведение

№

Название

Векторное выражение

Тензорное выражение

п/п

формулы

Задание вектора

a = a1e1 + a2e2 + a3e3

a = aiei

b = b1e1 + b2e2 + b3e3

b = biei

Определение

a b =

cosα

ai ai

bibi

aibi

скалярного

ai ai

bibi

произведения

Скалярное

a b = (a1e1 + a2e2 + a3e3 )

В прямоугольной системе

произведение,

(b1e1 + b2e2 + b3e3 ) =

aibi

= a jb j + ak bk

метрический тензор

В косоугольной системе

a1b1 + a2b2 + a3b3

g ij a

= g

aib j = a

bi = aib

a b = a1b1 + a2b2 + a3b3

Свойство 1.

a b = b a

aibi

= bi ai

(коммутативность)

Свойство 2..

(λ a) b = λ(b a)

(λ ai )bi

= λ(aibi )

(ассоциативность)

Свойство 3

(a +b) c = a c +b c

(ai + bi )ci

= aici

+bici

.(дистрибутивность)

Свойство 4.

a a > 0

при a ≠ 0

= δij ai a j

= ai ai

Квадрат вектора,

Символ Кронекера

a2 = g ij ai a j = gij ai a j = ai ai

Модуль вектора,

a =

δijaia j

aiai

символ Кронекера и

метрический тензор

a = g ij ai a j = gij ai a j = ai ai

Косинус угла

cosα =

a b

cosα =

ai bi

между двумя

ai ai

bibi

векторами

cos α =

g ij ai

g ij ai a j

g ij bi b j

g ij a i b j

g ij a i a j

g ij bi b j

ai a i

bi bi

Скалярное

= e

= δ

произведение

e1 e2 = e1 e3 = e2 e3 = 0

= gij ; eie j

= gij ;

базисных векторов

eie j

e e j

= g j

=δ j

Условие

a b = 0

= 0

ортогональности

Скалярное

a e1 = a1

a ei

= ak ek

= ak (ek ei )=

произведение

вектора на

a1e1e1 + a2e2e1 + a3e3e1 = a1

= a

gik

= ai

базисный вектор

Координаты

= cos

α1 e1 +

= cosαi

единичного вектора

+ cosα2 e2 + cosα3 e3

Проекция одного

a u

вектора на другой

прua =

uiui

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1311 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.03.20161.17 Mб53tau_dlya_chainikov.pdf
#
21.08.20191.28 Mб26td1.doc
#
21.04.2015943.1 Кб30td11.doc
#
18.09.2019273.41 Кб0tema4_1a.doc
#
22.08.2019451.02 Кб3Tema_1_2.docx
#
09.02.20151.52 Mб55Tensor-Gotman.pdf
#
10.02.201517.73 Mб44teopiya_tanka_sergeev.djvu
#
15.04.20195.54 Mб1teoria ответы.doc
#
23.09.201924.91 Mб6teoria-ilyukhina.docx
#
10.02.20153.26 Mб21teoria.pdf
#
10.02.20151.77 Mб7teoria_na_bilety_2013.pdf