Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Tensor-Gotman

.pdf

Скачиваний:

Добавлен:

09.02.2015

Размер:

1.52 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 133 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Определение 4.5 Ковариантные компоненты a1, a2 (индекс внизу) могут быть найдены

либо по составляющим a1

, a2

вектора a по направлениям взаимного базиса, либо

по ортогональным проекциям

вектора a на оси основного базиса (рис. 2.5).

Замечание 2.5. Получение ортогональных проекций на оси каждого базиса делается

следующим образом: получаются единичные векторы e

e ,

e1 e1 , e2

e2 ,

а тогда, например,

(1.5)

где

и есть проекция вектора а на ось e

и т.д (рис. 2.5).

Замечание 3.5 В системе координат, определяемой основным базисом (e1,e2 ,e3 ) ,

мы

имеем контравариантные компоненты ai

вектора a .

Замечание 4.5. Вспомним, что ковариантные компоненты получаются по формулам

a1 = a e1,

a2 = a e2 ,

a3 = a e3 ,

(2.5)

а контравариантные - по формулам

a1 = a e1,

a2 = a e2 ,

a3 = a e3 ,

(3.5)

где сам вектор a записывается через них по основному базису как

a = a1e1 + a2e2 + a3e3 ,

(4.5)

и по взаимному базису как

a = a1e1 + a2e2 + a3e3 .

(5.5)

Определим в новом базисе e'1 , e'2 , e'3 ковариантные компоненты ai'

вектора a через

его компоненты ai и контравариантные компоненты ai' - через ai . Вспомним, что

ai' i = e'i ei и

ai i' = ei e'i

(6.5)

Умножая обе части равенства (5.5) скалярно на вектор ei' , получим

ai' = a ei' = aieiei' = aiei'ei = ai'i ai

(7.5)

Это закон прямого преобразования. Аналогично получается закон обратного

преобразования Замечание 5.5 Название ковариантный связано с тем, что прямое преобразование

ковариантных компонент выполняется при помощи прямой матрицы A = ai'i

ai' = ai'i ai ,		(8.5)
и контравариантных компонент - при помощи той же матрицы
ai' = a	ai	(9.5)
i'i

Замечание 6.5 Для обратного преобразования применяется обратная матрица A−1 = ai i'

a = a	ii'	a	и ai = a	ii'	ai'	(10.5)
i	ii'	i'		ii'

Замечание 7.5 Важно отметить, что косоугольные декартовы координаты точки

следует писать с индексами вверху x1, x2 , x3 . Это становится ясным, если учесть, что

эти координаты являются контравариантными компонентами радиуса – вектора этой точки, так что

r = x1e1 + x2e2 + x3e3 = xk ek

(11.5)

Пример 1.5 Определить ковариантные компоненты данного тензора в системе K1'

Пусть в декартовой системе координат K (i1, i2 , i3 ) даны компоненты тензора 2-го ранга

Aik	=	A k	=	Ai	=	A	=	2	1	3	.	(i)
								2	3	4
								2	3	4
		i		k		ik		1	2	1
		i		k		ik

Базисные векторы координатной системs K1' выражаются через базисные векторы декартовой системы по следующим формулам:

e1 = i1

e2 = i1 + i2

(ii)

e3 = i1 + i2 + i3

Определение ковариантных компонент A'

делается по формулам

= αl

α m A

(iii)

где

αl , α m

- коэффициенты прямого преобразования. Коэффициенты αl

имеют вид

α11' =1, α12' = 0, α13' = 0,

α12'

=1,

α22' =1, α23' = 0,

(iv)

таким образом, получим

α31' =1, α32' =1, α33' =1.

= α1

α1 A +α1 α 2 A +α

1 α3 A =1 1 2 +1 0 1+1 0 3 = 2 ,

1' 1' 11

1' 1' 12

= α1

α1

A +α1

α 2

A +α1

A =1 1 2 +1 1 1 +1 0 3 = 2 +1 = 3

= α1

α1

A +α1

α 2 A +α1

3 A =1 1 2 +1 0 1 +1 1 3 = 6

1' 3' 11

1' 3' 12

так как α12' = 0,

α13'

= 0,

то суммирование по l в этих формулах не выполняется.

=α1

1 A

+α1

α2 A

+α1

α3 A

+α22' α11' A21 +α22' α12' A22 +α22' α13' A23 =

=1 1 2 +1 0 1 +1 0 3 +1 1 2 +1 0 3 +1 0 4 = 2 + 2 = 4

A22' =α12' α12' A11 +α12' α22' A12 +α12' α23' A13 +

+α22' α12' A21 +α22' α22' A22 +α22' α23' A23 =

=1 1 2 +1 1 1 +1 0 3 +1 1 2 +1 1 3 +1 0 4 = 2 +1 + 2 + 3 = 8

A23' = α12' α31' A11 +α12' α32' A12 +α12' α33' A13 +

+α22' α31' A21 +α22' α32' A22 +α22' α33' A23 =

=1 1 2 +1 1 1 +1 1 3 +1 1 2 +1 1 3 +1 1 4 = 2 +1 + 3 + 2 + 3 + 4 =15

A31' = α31' α11' A11 +α31' α12' A12 +α31' α13' A13 +

+α3'2 α1'1 A21 +α3'2 α1'2 A22 +α3'2 α1'3 A23 +

+α33' α11' A31 +α33' α12' A32 +α33' α13' A33 =

=1 1 2 +1 0 1 +1 0 3 +1 1 2 +1 0 3 +1 0 4 +1 1 1 +1 0 2 +1 0 1 = 2 + 2 +1 = 5

A32' = α 31' α 12 ' A11 + α 31' α 22' A12 + α 31' α 23' A13 +

+ α 32' α 12 ' A21 + α 32' α 22' A22 + α 32' α 23' A23 +

+ α 33' α 12 ' A31 + α 33' α 22' A32 + α 33' α 23' A33 =

= 1 1 2 + 1 1 1 + 1 0 3 + 1 1 2 + 1 1 3 + 1 0 4 + 1 1 1 + 1 1 2 + 1 0 1 =

2 + 1 + 2 + 3 + 1 + 2 = 11

A33' = α31' α31' A11 +α31' α32' A12 +α31' α33' A13 +

+α32' α31' A21 +α32' α32' A22 +α32' α33' A23 +

+α33' α31' A31 +α33' α32' A32 +α33' α33' A33 =

=1 1 2 +1 1 1 +1 1 3 +1 1 2 +1 1 3 +1 1 4 +1 1 1+1 1 2 +1 1 1 =

=2 +1+ 3 + 2 + 3 + 4 +1 + 2 +1 =19

Таким образом, ковариантные компоненты равны:

2		3	6
A'ik	= 4	8	15	(v)

511 19

§6. Индексные обозначения и соглашение о суммировании

Правило индексных обозначений

Рассмотрим сокращенные написания тензоров, например, таких как ai jb j , εi jk uiυk .

Для того, чтобы легко читать работы, в которых используются тензоры, необходимо знать правила написания индексов.

1)Буквенный индекс в каждом члене может встречаться один или два раза.

2)Если индекс встречается один раз, то подразумевается, что он принимает значения натурального ряда 1, 2, 3, …, N . N - заданное положительное целое число, которое определяет размерность индекса, то есть, интервал его изменения. Размерность индекса

определяет размерность пространства, в котором решается задача.

3)Неповторяющиеся индексы называются свободными.

4)Тензорный ранг данного члена определяется числом свободных индексов в этом

члене.

5)Правильно написанные тензорные соотношения имеют одинаковые свободные индексы в каждом члене.

Пример 1.6 В трёхмерном пространстве расшифровать следующие тензорные символы:

1) Ai i , 2) Bi j j , 3) Ri j , 4) aiTi j , 5) aib j Si j .

Решение:

1)Ai i = A11 + A22 + A33 .

2)Bi j j представляет три суммы

при i =1 B111 + B122 + B133 , при i = 2 B211 + B222 + B233 , при i = 3 B311 + B322 + B333 .

3)Ri j , представляет 9 компонент R11 , R12 , R13 , R21 , R22 , R23 , R31 , R32 , R33 . .

4)aiTi j представляет три суммы:

при j =1

a1T11 + a2T21 + a3T31 ,


при j = 2		a1T12 + a2T22 + a3T32 ,
при j = 3		a1T13 + a2T23 + a3T33 .
Пример 2.6		В трёхмерном пространстве вычислить следующие выражения, содержащие
дельту Кронекера δi j 1) δi i 2) δi jδi j 3) δi jδi kδ j k 4) δi jδ j k 5) δi j Ai k
1)	δi i = δ11 +δ22 +δ33 = 3
2)	δi jδi j = δ1 jδ1 j +δ2 jδ2 j +δ3 jδ3 j = 3
3)	δi jδi kδ j k = δ1 jδ1kδ j k +δ2 jδ2 kδ j k +δ3 jδ3 kδ j k = 3

4) δi jδ j k = δi1δ1k +δi 2δ2 k +δi 3δ3k = δi k 5) δi j Ai k = δ1 j A1k +δ2 j A2 k +δ3 j A3k = Aj k

Соглашение о суммировании А. Эйнштейна.

Соглашение о суммировании состоит в том, что если индекс употребляется дважды, то этот индекс принимает все значения из своего интервала изменения, и

члены, соответствующие каждому значению индекса из этого набора, суммируются.

Правило 1.6

1)Повторяющиеся индексы называют немыми, так как их замена на любые другие буквы, не использованные в качестве свободных индексов, не меняет значения членов, в которые они входят.

2)В правильно написанном тензорном выражении ни один индекс не встречается

более двух раз.

3)Если в некотором выражении какой-нибудь индекс приходится писать более, чем дважды, соглашение о суммировании не используется.

4)Тензоры первого ранга (векторы) обозначаются основной буквой с одним свободным индексом, то есть, в виде

ai или bi .

5) В следующих выражениях, имеющих один свободный индекс, можно узнать тензоры первого ранга (векторы)

a	i j	b	j	, F	, R p	, ε	i jk	u υ	.
	i j		j	ik k	.qp		i jk	i k

так как в каждом из них после выполнения суммирования останется по одному индексу. 6) Тензоры второго ранга обозначаются буквами с двумя свободными индексами. Так

произвольный тензор второго ранга Т будет записан в одной из четырёх возможных форм

T i j , Ti j или T.ij , Ti j .

Всмешанной форме точка указывает на то, что индекс j - второй по порядку.

7)Тензорные величины второго ранга могут выглядеть по-разному, например, так:

a	i ji p	, bi j	,	δ	i j	u	k	υ	k	.
	i ji p	,, j k			i j		k		k

Здесь после выполнения суммирования по одинаковому индексу останутся по два свободных индекса, что даёт тензор второго ранга.

8)Продолжая логически эту цепочку, получим, что тензор третьего ранга записывают

стремя свободными индексами.

9)Символ, который не имеет связанного с ним индекса, изображает скаляр, то есть, тензор нулевого ранга.

Замечание 1.6 Соглашение о суммировании часто используют в связи с представлением векторов в символических обозначениях через базисные векторы,

снабжённые индексами. Так, если декартовы оси и единичные векторы базиса,

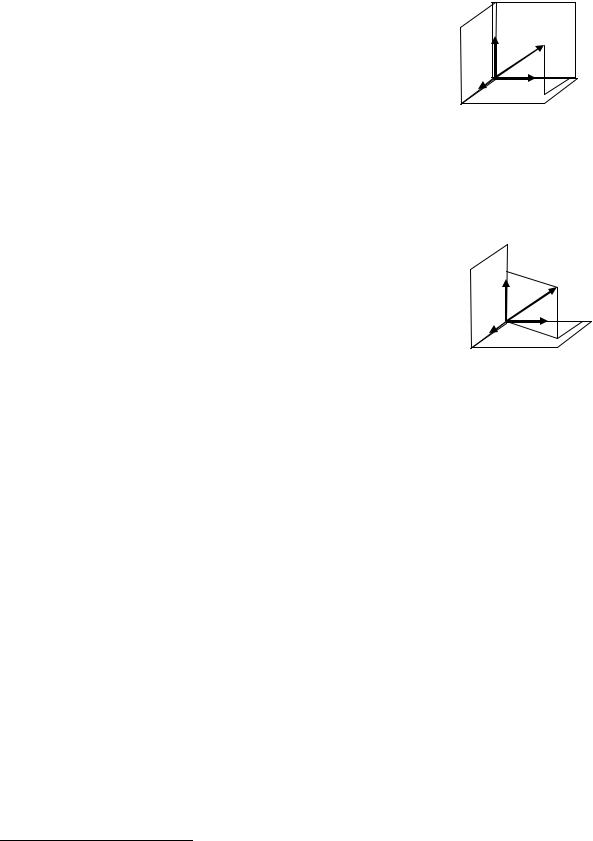
изображённые на рис. 1.6, переобозначить,		как на рис. 2.6, то произвольный вектор
v =υ1i +υ2 j +υ3k	можно записать в виде
	v =υ1e1 +υ2e2 +υ3e3	(1.6)
где υ1, υ2 , υ3 -	декартовы координаты	вектора v.

Применяя к этому равенству соглашение о суммировании, его можно переписать в сокращённом виде

v =υiei

(2.6)

где i - индекс суммирования. При таком сочетании обозначений не действует правило повторяющихся индексов, принятое в чисто индексном обозначении тензорных величин.

Тензоры второго ранга тоже могут быть представлены суммированием по базисным векторам, снабжённым индексами. Так, диаду ab 1, заданную в девятизначной форме, можно записать в виде

z
k		v
i	j	y
i		y

Рис. 1.6 Вектор v в декартовой системе координат

ab = (aiei )(b je j ) = aib jeie j

Замечание 2.6 В этом выражении важно сохранять порядок написания базисных векторов.

Девятичленная форма любого тензора второго ранга D может быть представлена в компактном обозначении так:

D = Dijeie j

(4.6)

Пример 3.6 Пусть даны два произвольных тензора aijk и

		(3.6)
x3
	e3		v
e1		e2		x2

blm ранга 3 и 2.		x1
		Рис. 2.6 Вектор v в
1.	Определить ранг произведения aijk blm .
		обобщённой системе
2.	Получить из них тензор третьего ранга и свернуть	координат

	его по индексам k и l .
3.	Получить из произведения этих тензоров тензор первого ранга.

Решение.

1.Ранг произведения aijk blm равен 3 + 2 = 5.

2.Для уменьшения ранга на 2 единицы нужно произвести свёртывание по каждой паре индексов, принадлежащих разным сомножителям. При этом получается 6 тензоров

aijk bim , aijk bli , aijk b jm , aijk blj , aijk bkm , aijk blk

третьего ранга, потому что в каждом из них остаётся только по три свободных индекса.

3.Для получения тензора первого ранга достаточно тензор третьего ранга свернуть по индексам i , j и m , то есть,

aijk bij , aijk b ji , aijk b jk , aijk bkj , aijk bki , aijk bik ,

в каждом из них только по одному свободному индексу, и из каждого получается один и тот же тензор ak b первого ранга.

Задача 1.6 Свёртывание произведения произвольного тензора aijk с единичным тензором δij

Решение.

aijkδkl = aij1δ1l + aij2δ2l + aij3δ3l = aijl

1 Подробно понятие диады рассматривается в главе 2.

Как и следовало ожидать, получился исходный тензор, так как δij равен единице только в том случае, когда k = l .

Замечание 3.6 Операция свёртывания используется для получения обратного

тензорного признака.

В обычном физическом пространстве базис состоит из трёх некомпланарных векторов, и любой вектор в этом пространстве задаётся своими тремя компонентами. Поэтому индексы у величин ai принимают значения 1, 2, 3, и ai представляет сразу три

компоненты a1, a2 , a3 .

Замечание 4.6 Символ ai можно толковать в одном случае как i - тую компоненту

вектора а, а в другом - как сам вектор.

В трёхмерном пространстве, где оба индекса i и j меняются от 1 до 3, символ ai j

представляют девять компонент тензора второго ранга. Подробно, в виде квадратной таблицы это выглядит так:

a11

ai j = a21

a31

a12 a22 a32

a
13
a23		(5.6)

a33

Таким же образом компоненты тензора первого ранга (вектора) в трёхмерном пространстве можно наглядно изобразить упорядоченной строкой или столбцом из компонент в виде

		a
ai = (a1 a2	a3 ) или ai	1
ai = (a1 a2	a3 ) или ai	= a2	(6.6)

		a3

10)В общем случае в N - мерном пространстве тензор n -го ранга будет иметь N n компонент;

11)Удобство индексных обозначений для записи систем равенств иллюстрируется двумя примерами. В трёхмерном пространстве уравнение в индексной записи имеет вид

		xi = ci j z j ,													(7.6)
а в развёрнутом виде три уравнения
x		= c z		+ c z			2		+ c z			3
1		11 1		12			2		13			3
x2 = c21z1 + c22 z2 + c23 z3															(8.6)
x	3	= c	z	+ c	32	z		2	+ c	33	z		3
	3		31 1		32			2		33			3
12) Если i и j принимают значения 1									и 2, то, например,					равенство в индексной
записи		ai j = bi p c j q d pq													(9.6)
		ai j = bi p c j q d pq													(9.6)
в развёрнутой форме даёт четыре соотношения:
a11 = b11c11d11 + b11c12 d12 + b12c11d21 +b12c12 d22 ,
a12 = b11c21d11 + b11c22 d12 + b12c21d21 + b12c22 d22														,	(10.6)
a21 = b21c11d11 + b21c12 d12 +b22c11d21 + b22c12 d22 ,															(10.6)
a21 = b21c11d11 + b21c12 d12 +b22c11d21 + b22c12 d22 ,

a22 = b21c21d11 + b21c22 d12 + b12c21d21 +b22c22 d22 .

Если же i, j =1, 2,3, то формула (10.6) даст девять соотношений, каждое из которых имеет девять членов в правой части.

13) Если нужно уточнить, какие значения пробегает греческий индекс, то эти

значения заключаются в угловые скобки.
aαeα α =1,2,3	(11.6)

Замечание 5.6 В прямоугольной декартовой системе координат ковариантные и контравариантные компоненты совпадают Замечание 6.6 Для верхних и нижних индексов существуют правила, которое используется для проверки формул:

Правило 2.6 Суммирование может производиться только по верхнему и нижнему «немым» индексам. Запись aibi , aik ak является верной. ak bk , aik ak - неверные записи (в обобщённой системе координат!).

Правило 3.6 Формула ai = aik ak называется операцией «опускания» индекса, а формула

ai = a i k ak - «поднятия» индекса.

Замечание 7.6 Эти правила относятся к компонентам тензоров в обобщённых системах координат. В прямоугольной декартовой системе допустимы записи Aik Bi , Cik Ak и

т.п., потому что основной и взаимный базисы совпадают.

§ 7 Связь между ковариантными и контравариантными компонентами вектора.

Для простоты на рисунках 1.5 и 2.5 были показаны только по две компоненты вектора в каждой системе. Выражение ковариантных компонент ak вектора через его

контравариантные ak компоненты в пространстве можно получить, если разложение

a = a1e1 + a2e2 + a3e3 = ∑ak ek			= ak ek	(1.7)
умножить скалярно на ei	k =1
умножить скалярно на ei
a e i = a k ( e k			e i )	(2.7)
и наоборот, контравариантные ak	компоненты можно выразить через ковариантные
ak			3
			3
a = a1e1 + a2e2 + a3e3 = ∑ak ek = ak ek				(3.7)
			k =1
если умножить скалярно на ei
a ei = ak ( ek ei )				(4.7)
Введём обозначения		= ek ei
gk i = gi k		= ek ei		(5.7)
g ki = g ik		=ek ei		(6.7)
Тогда, учитывая, что a ei = ai и a ei = ai , из (4.7) и (2.7) получим
ai	= g i k ak ,			(7.7)
ai	= gi k ak ,			(8.7)

которые и дают искомые выражения для связи компонентов вектора а. Эти действия называются действиями подъёма и опускания индекса с помощью метрического

тензора.

Кроме выражений (5.7) и (6.7) вводится обозначение для выражения взаимности базисов:

e	k	k		k		0, если	i ≠ k	(9.7)
		ei = gi	= δi		=		i = k
						1, если
Определение 1.7 Каждое из выражений				gi k		и g i k	представляет собой тензор второго

ранга и, так как они определяют метрику пространства, их называют метрическими

тензорами

Замечание 1.7 Дельта Кронекера gik = δik также тензор

Авторого ранга.


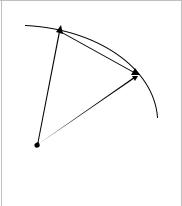
∆S		Рассмотрим некоторые свойства величин gi k ,				g i k	и gik .
∆r	В	Они важны,			так как являются основной характеристикой
r	В	пространства,			связанного базисом (e1, e2 ,e3 ) .	Это	легко
r + ∆r		понять, если			выразить приращение длины дуги	∆S	через
r + ∆r		числа gi k и g i k . Приращение длины дуги можно заменить,
О		числа gi k и g i k . Приращение длины дуги можно заменить,
О		как всегда в математическом анализе, приращением радиуса –
Рис. 1.7 К понятию		как всегда в математическом анализе, приращением радиуса –
длины дуги		вектора	∆r	(рис. 1.7). Отсюда
длины дуги		вектора	∆r	(рис. 1.7). Отсюда

	(∆S)2	=	∆r	2 ,	(10.7)

где ∆r = ei ∆xi , ∆r = ek ∆xk , что, в силу инвариантности длины отрезка, можно написать
в виде
(∆ S)2 = (∆r) (∆r) = ei ∆xi ek ∆xk		= ei ∆xi ek ∆xk = ei ∆xi ek ∆xk			(11.7)

где ∆xi , ∆xi - компоненты вектора ∆r в основном и взаимном базисах. Тогда, используя обозначения (5.7) и (6.7), можно записать

(∆S)2 = gi k ∆xi ∆xk	(12.7)
или
(∆S)2 = g i k ∆xi ∆xk	(12’.7)
или
(∆S)2 = ∆xi ∆xi ,	(12’’.7)
где ∆xi , ∆xk - ковариантные компоненты вектора	∆r , а ∆xi , ∆xk - контравариантные
компоненты вектора ∆r .

Формулы (12.7), (12’.7) и (12’’.7) определяют квадрат элемента дуги в выбранной

системе координат через метрические тензоры gi k	(или g i k ).
Определение 2.7 Говорят, что величины gi k	(или g i k ) определяют метрику

пространства, арифметические свойства которого устанавливаются введённой системой координат х1, x2 , x3 .

Связь между величинами gi k и g i k можно установить, если рассмотреть выражения ai = gik ak ( i =1,2,3 )

как систему трёх линейных относительно ak уравнений:

a1 = g11a1 + g12a2 + g13a3,

a2 = g21a1 + g22a2 + g23a3,					(13.7)
a3 = g31a1 + g32a2 + g33a3
Для решения этой системы введём обозначение определителя этой системы
	g11	g12	g13
G = det(gik ) =	g21	g22	g23	,	(14.7)
	g31	g32	g33

где (gik ) - матрица

g11

(gik ) = g21

g31

g12 g22 g32

	g13
	g23		(15.7)
			(15.7)


	g33

Отсюда, решая систему (13.7) по Крамеру, получим

g12

g13

g22

g23

∑G1k ak

a1 =

g32

g33

k =1

g11

g13

g21 a2

g23

∑G2 k ak

a2 =

g31 a3

g33

k =1

g11

g12

g21

g22

∑G3 k ak

a3 =

g31

g32

k =1

или

ai =

∑Gi k ak

Gi k ak

k =1

( i =1,2,3 )

гдеGi k - алгебраические дополнения,

соответствующие члену

(определителя) G , могут быть записаны в виде

Gik =

g ps

g pt

gr s

grt

(16.7)

(17.7)

(18.7)

(19.7)

(gik ) детерминанта

(20.7)

где индексы (i, p, r) и (k, s, t) составляют циклическую перестановку чисел 1, 2, 3. Таким образом, например, имеем

G11 =

g22

g23

, G12 =

g13

g12

, G13 =

g12

g13

. .

g32

g33

g32

g22

g23

g12

g13

∑Gi k ak получается из определителя

g22

g23

k =1

g32

g33

g22

g23

g13

g12

g13

∑G1k ak

= a1

+ a2

+ a3

= a1G11 + a2G12 + a3G13

(21.7)

k =1

g32

g33

g32

g22

g23

То есть, ai =

∑Gi k

k =1

или по соглашению о суммировании

Gi k

ak .

(22.7)

Сравнивая теперь (19.7) с (7.7), получим искомую связь

g ik =

∑Gi k

g ik

Gik

k =1

или

(23.7)

Аналогичным путём можно получить выражение

∑Gik

Gik

gik =

k =1

или gik

(24.7)

G '

где

g ps

g pt

G'= det g ik ,

(25.7)

g r s

g rt

С другой стороны,

непосредственными вычислениями с учётом (5.7), (6.7) и (9.7)

ek ei = gi k = gk i

ei = g i k

= g ki

(26.7)

0, если

i ≠ k

ei = gi = δi =

= k

и полученных ранее в § 3 выражений

1, если

e j ×ek

(27.7)

el (em ×en )

можно выяснить геометрический смысл знаменателя G .

Подставим выражения (27.7) в формулу (26.7) и используем свойство векторно – векторного произведения 2 Тогда получается

g i k = ei ek =

e p ×er

es ×et

e p es

e p et

g p s

g p t

(28.7)

V 2

er es

V 2

gr s

gr t

er et

где (i, j, k) и (l, m, n) составляют циклические перестановки чисел 1, 2, 3..

g11

g12

g13

а Gi k

g p s g p t

G = det(g

) = g

gr s

gr t

g32

g33

g31

Сравнивая выражение (28.7) для g ik с (23.7), получим

2 a × (b × c) = b (a c) −c (a b) , откуда

(e p ×er ) (es ×et ) = et ×(e p ×er ) es ={e p (et er ) −er (et e p )}es = = (e p es )(et er ) − (er es )(et e p )

<<< < Предыдущая 1 23 / 133 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.03.20161.17 Mб53tau_dlya_chainikov.pdf
#
21.08.20191.28 Mб26td1.doc
#
21.04.2015943.1 Кб30td11.doc
#
18.09.2019273.41 Кб0tema4_1a.doc
#
22.08.2019451.02 Кб3Tema_1_2.docx
#
09.02.20151.52 Mб55Tensor-Gotman.pdf
#
10.02.201517.73 Mб44teopiya_tanka_sergeev.djvu
#
15.04.20195.54 Mб1teoria ответы.doc
#
23.09.201924.91 Mб6teoria-ilyukhina.docx
#
10.02.20153.26 Mб21teoria.pdf
#
10.02.20151.77 Mб7teoria_na_bilety_2013.pdf