
Tensor-Gotman
.pdf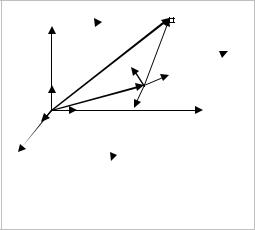
Вывод: Отсюда ясно, что для каждого значения индекса |
i |
(i =1,2,3) |
|
имеют место |
|||||||||||||||
следующие 18 соотношений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
0, |
i'≠ j', |
|
|
|
|
|
|
|
|
|
|
|
|
||
∑αim' αmj' |
= δi'j' |
|
|
|
|
|
|
|
|
(iv) |
|||||||||
= |
i'= j'. |
|
|
|
|
|
|
|
|
|
|||||||||
m=1 |
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
m' |
j |
0, |
i ≠ j, |
|
|
j |
|
|
|
|
|
|
|
|
|
||
∑ |
|
= |
δ |
|
|
|
|
|
|
|
|
(v) |
|||||||
αi α |
m' |
= |
i = j. |
|
i |
|
|
|
|
|
|
|
|
||||||
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
m'=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверка показывает |
|
3 |
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
e'i = ∑e'k |
∑αim' αmk' = ∑δi'k' e'k |
, |
|
|
|
|
|
|
|
(vi) |
|||||||||
|
|
k =1 |
|
m=1 |
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ei = ∑ek |
∑αim'αmk ' = ∑δik ek |
, |
|
|
|
|
|
|
|
(vii) |
|||||||||
|
|
k =1 |
m'=1 |
k =1 |
|
|
|
|
|
|
|
|
|
|
|
||||
что подтверждает корректность преобразований. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Вторая основная задача |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть в пространстве введены две прямоугольные декартовы системы координат (К) и |
|||||||||||||||||||
(K ') . Задача заключается в том, чтобы выразить координаты (x1, x2 , x3 ) |
|
произвольной |
|||||||||||||||||
точки М в системе (К) через координаты (x' |
, x' |
, x' ) системы (K') и наоборот (рис. 2.2). |
|||||||||||||||||
|
|
|
|
|
1 |
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
Решение. Пусть r и r’ – соответственно радиусы – векторы |
точки М в системах (К) и |
||||||||||||||||||
(K') , орты которых (e1,e2 ,e3 ) и (e'1 ,e'2 ,e'3 ) . Положение начала координат О1 системы |
|||||||||||||||||||
(K') в системе (К) определяется радиусом – вектором r'o , так что r |
|
= −r' |
o |
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Пусть αi'k - косинус угла между i - той осью системы (K ') |
и k - той осью системы (К) |
||||||||||||||||||
так, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αi'k = cos(x'i , xk ) = ei ek . |
(i) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М |
|
|
r = r'+ro1 ; |
|
|
|
|
|
|
|
|
x3' |
|
|
|
|
|
|||||
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
x' |
||||||
r' = r +r'o |
|
|
|
|
|
|
|
|
r |
|
|
|
r’ |
|
|
||||
Используя выражение для радиуса – вектора, |
|
|
|
|
|
|
ro1 e3' |
|
(K’) |
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
e2' |
|
||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
e3 |
|
|
O1 |
|
||||
xk ek = x'k e'k +xko1ek |
|
|
|
|
|
|
|
(К) |
|
|
|
|
' |
|
|
x2 |
|||
|
|
(ii) |
|
|
|
|
e1 |
О |
e2 |
|
|
|
e1 |
|
|
||||
x'k e'k = xk ek + x'o e'k |
|
|
(iii) |
|
|
|
|
x1 |
|
|
|
x' |
|
|
|
|
|
||
(Нужно помнить, что |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
Рис. 2.2 |
К преобразованию |
|
|||||||
xk ek = ∑xk ek = x1e1 + x2e2 + x3e3 ). |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
координат точки М |
|
|
|||||||||||
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Умножая (ii) скалярно на ei , а (iii) на e'i |
и используя свойства скалярного произведения |
||||||||||||||||||
векторов |
|
|
|
0, |
i ≠ k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ei ek = |
i = k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а также (i), получим |
|
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11
|
|
|
|
xi = (e'k ei ) x'k +xko1 = αk'i x'k +xko1; |
|
|
|||||||||
|
|
|
|
xi' = (ek e'i ) xk + x'io = αi'k xk + x'io . |
|
|
|||||||||
Эти выражения и дают формулы |
линейного ортогонального преобразования координат |
||||||||||||||
точки. Коэффициенты этих формул удовлетворяют условиям ортогональности. Эти |
|||||||||||||||
условия можно получить, используя формулы |
|
|
|
|
|
|
|||||||||
и отсюда |
|
|
|
a e1 = a1, a e2 = a2 , a e3 = a3 |
|
|
|
||||||||
|
|
|
a = (a e1)e1 + (a e2 )e2 + (a e3 )e3 |
|
|
(iv) |
|||||||||
|
|
|
|
|
|
||||||||||
для разложения ортов ek |
системы (К) по ортам e'k |
системы (K ') |
и ортов e'k |
по ортам ek . |
|||||||||||
Полагая в (iv) a = ei ', получим |
|
|
|
|
|
|
|
|
|
|
|||||
Аналогично получим |
ei '= (ei ' el )el = αi'l el . |
|
|
|
|
|
|||||||||
ei = (ei el ')el '=αl'iel ' . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
Умножая первое |
разложение |
скалярно |
на e'k , |
а второе |
- |
на ek , |
и используя |
||||||||
0, |
i ≠ k |
получим |
|
|
|
|
|
|
|
|
|
|
|
||
ei ek = |
i |
= k |
|
|
|
|
|
|
|
|
|
|
|
||
1, |
|
ei ' ek '= αi'l .αk'l .; |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
ei ek =αl'i .αl'k .. |
|
|
|
|
|
|
|||||
Вводя символ (дельту) Кронекера |
|
i ≠ k |
|
|
|
|
|
|
|||||||
|
|
|
|
δik |
0, если |
, |
|
|
|
|
|
||||
|
|
|
|
= |
|
i = k |
|
|
|
|
|
||||
получим |
|
|
|
|
|
1, если |
|
|
|
|
|
|
|||
|
|
|
|
|
|
αi'l .αk'l . = δik' |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
, |
|
|
|
|
(v) |
|||
|
|
|
|
|
|
|
αl'i .αl'k' = δik . |
|
|
|
|
|
|||
Эти формулы доказывают ортогональность выполненного преобразования. |
|
||||||||||||||
|
|
|
|
§ 3. Реперы и кореперы в пространстве |
|
||||||||||
Проекции вектора на прямоугольные координаты |
|
i3 |
|
|
|||||||||||
Пусть |
вектор |
задан |
в |
виде |
суммы |
своих |
O |
|
i 2 |
|
|||||
компонентов (рис. 1.3) |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
i1 |
|
|
|||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
a |
a3 |
|
|
|
|
|
a = ∑ak |
|
|
(1.3) |
|
|
O |
|||||
|
|
|
|
|
|
|
a1 |
|
|||||||
Проекции |
|
|
а |
|
k =1 |
|
|
|
|
|
|
|
|||
вектора |
на |
оси |
прямоугольной |
|
|
a2 |
|
||||||||
системы координат определяются в виде скалярных |
|
|
|
||||||||||||
|
|
|
|
||||||||||||
произведений этого вектора а на соответствующие |
Рис. 1.3 Компоненты вектора |
||||||||||||||
орты i1, i2, i3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 = а · i1, |
a2 = а · i2 |
a3 = а · i3. |
(2.3) |
|
|
a ik = ik прi k a = ak . |
||||||||
так как по формуле (2.2) легко получить проекцию на орт в виде |
|||||||||||||||
Замечание 1.3 |
Следует помнить, что компоненты a1 a2 |
a3 вектора а (1.3) направлены по |
|||||||||||||
ортам i1, i2, i3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если выразить орты i1, i2, |
i3 как частное в виде i1 = a1 a1 , |
i 2 |
= a2 a2 и i3 = a3 a3 , то |
||||||||||||
вектор а в прямоугольной системе координат можно записать в виде |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |

|
3 |
|
3 |
|
|
3 |
|
|
3 |
ak ) ak |
3 |
|
|
|
|
a = ∑ ak = ∑ak |
ak |
= ∑(a ik ) ak = ∑(a |
= ∑(a ak2 )ak |
(3.3) |
|||||||||||
|
k =1 |
|
k =1 |
|
ak |
k =1 |
|
ak |
k =1 |
ak |
ak |
k =1 |
ak |
|
|
Замечание 2.3 Равенство (3.3) было рассмотрено для прямоугольной системы |
|||||||||||||||
координат, а задача состоит в том, чтобы определить компоненты вектора в |
|||||||||||||||
произвольном базисе. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Проекции вектора на оси пространственных координат |
|
|
|
|
|||||||||||
Определение 1.3 Два базиса реперы (e1,e2 ,e3) и |
|
|
|
|
|||||||||||
кореперы ( e1,e2 ,e3 ) |
называются взаимными, если их |
|
е3 |
|
|
||||||||||
векторы удовлетворяют условию |
|
|
|
|
|
е3 |
|
е2 |
|
||||||
|
0, |
|
если |
i ≠ k |
|
|
|
(4.3) |
h |
|
|||||
ei ek = |
если |
i = k |
|
|
|
|
|
е2 |
|
||||||
|
1 |
|
|
|
|
|
|
|
|
||||||
Замечание 3.3 Векторы |
ek (реперы) |
расположены под |
|
|
|
|
|||||||||
произвольными углами друг к другу, |
и их модули не |
|
|
е1 |
|
||||||||||
обязательно равны единице. |
ei ek |
|
|
|
|
|
|
|
|
||||||
Замечание 4.3 Из равенства |
= 0 , |
если |
i ≠ k , |
|
|
|
е1 |
||||||||
следует, |
что |
каждый |
вектор |
одного |
базиса |
|
Рис. 2.3 |
Связь основного и |
|||||||
перпендикулярен |
|
к |
двум |
векторам |
другого |
базиса |
|
||||||||
|
|
|
взаимного базисов |
||||||||||||
(например, |
e1 e2 |
и |
|
e1 e3 , |
а это |
значит, что |
он |
|
|
|
|
||||
перпендикулярен плоскости векторов e2 и e3 ), а |
с |
третьим вектором, с которым |
|||||||||||||
совпадает его индекс, он составляет острый угол (потому что их произведение равно |
|||||||||||||||
положительному числу). |
|
|
|
|
|
|
|
|
|
|
|
||||
Замечание 5.3 Если на двух взаимных базисах построить параллелепипеды с объёмами |
|||||||||||||||
V = |
|
e |
1 |
(e |
2 |
×e |
3 |
) |
|
и V 1 = |
e1 (e2 |
×e3 ) |
, то рёбра одного из них будут перпендикулярны к |
||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
граням другого и наоборот (рис. 2.3).. |
|
|
|
|
|||||||||||||||||||||||||||
Например, e3 e3 = |
|
e3 |
|
|
|
e3 |
|
|
|
cos(e3 ,e3 ) =1 означает, что |
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e3 |
|
|
= |
|
|
|
1 |
= |
1 |
|
(5.3) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e3 |
|
cos(e3 ,e3 ) |
h |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где h = e3 cos(e3 ,e3 )
Отсюда следует, что модули векторов одного базиса равны обратным значениям
параллельным им высот параллелепипеда взаимного базиса.
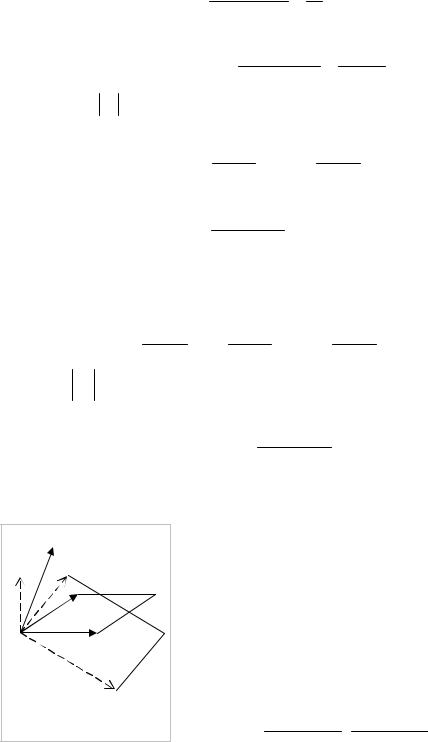
Построение взаимного базиса.
Пусть дан базис (e |
,e |
2 |
,e |
3 |
) . Вектор e1 |
взаимного базиса должен быть |
1 |
|
|
|
|
||
перпендикулярен к векторам e2 и e3 , т.е. параллелен их векторному произведению |
||||||
|
|
|
|
e1 = m (e2 ×e3 ) |
(6.3) |
|
Скаляр m определяется из условия |
|
|
||||
т.е. |
|
|
|
e1 e1 =1, |
(7.3) |
|
|
|
|
me1 (e2 ×e3 ) =1 |
(8.3) |
||
|
|
|
|
|||
13
Поскольку |
смешанное |
произведение |
e1 (e2 ×e3 ) ≠ 0 , |
(так |
как |
|
векторы |
(e1,e2 ,e3 ) |
|||||||||||||||||||||||||||||
составляют базис) получим |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
m = |
e |
|
(e |
×e |
|
) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
(9.3) |
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
2 |
3 |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Это выражение используется далее в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
= e |
e2 ×e3 |
|
|
|
|
e2 ×e3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
e |
|
(e |
2 |
×e |
3 |
) |
= |
|
|
V |
|
. |
|
|
|
|
|
(10.3) |
|
|
||||||||||
Здесь модуль V1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
равен |
объёму параллелепипеда, |
|
построенного |
|
на векторах |
базиса |
|||||||||||||||||||||||||||||||
(e1,e2 ,e3 ) . Аналогично строятся векторы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
e2 = e3 ×e1 |
и |
|
e3 = e1 ×e2 . |
|
|
|
|
|
|
|
(11.3) |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 6.3 Соотношения (10.3) и (11.3) можно записать короче: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
ei = |
|
|
|
e j ×ek |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12.3) |
|
|
|||||||
|
|
|
|
|
el |
(em ×en ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где (i, j, k) |
и (l, m, n) составляют циклические перестановки чисел 1, 2, 3. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Полученные формулы дают выражения кореперов e1,e2 ,e3 через реперы e ,e |
2 |
,e |
3 |
. |
|||||||||||||||||||||||||||||||||
Аналогично получаются реперы через кореперы.: |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
e |
= e2 ×e3 |
. e |
2 |
= e3 ×e1 |
|
|
и |
e |
3 |
= e1 ×e2 . |
|
|
|
|
|
|
(13.3) |
|
|
|||||||||||||||||
|
1 |
|
V 1 |
|
|
|
|
V1 |
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где модуль V 1 равен объёму параллелепипеда, построенного на кореперах |
(e1,e2 ,e3 ) . |
|
|||||||||||||||||||||||||||||||||||
Сокращенная запись выражений (13.3) аналогична выражению (12.3) и имеет вид |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ei = |
e j ×ek |
|
|
|
|
|
|
|
|
|
|
|
|
(14.3) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
el (em ×en ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Свойства взаимных базисов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
е3 |
|
|
|
Свойство 1. |
Если e ,e |
2 |
,e |
3 |
- орты прямоугольной системы |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
е3 |
е2 |
|
|
координат, то взаимный к нему базис |
e1,e2 ,e3 |
совпадает с |
|||||||||||||||||||||||||||||||
|
е2 |
|
|
основным, то есть, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
e1 = e1 = i1, |
|
|
e2 |
= e2 = i 2 , |
e3 = e3 = i3 . |
|
(15.3) |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
е1 |
|
|
Свойство 2. |
Взаимные базисы либо оба правые, либо оба |
||||||||||||||||||||||||||||||||
|
|
|
|
левые (рис. 3.3).. |
|
|
|
|
|
|
|
что V1 V 1 =1, |
|
|
|
|
|
|
|
|
|||||||||||||||||
е1 |
|
|
|
|
|
Это следует из того, |
что в свою очередь |
||||||||||||||||||||||||||||||
Рис. 3.3 Взаимные |
|
|
получается из формулы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
e j ×ek |
|
|
|
e j |
×ek |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
базисы |
|
|
|
|
|
|
ei |
ei |
= |
|
|
|
=1 |
|
|
|
(16.3) |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
el (em ×en ) |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
el (em |
×en ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Д о к а з а т е л ь с т в о формулы V V 1 =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из известной формулы скалярного произведения двух векторных произведений |
|
|
|
|
|
||||||||||||||||||||||||||||||||
(a ×b) (c ×d) = (a c) (b d) −(a d) (b c) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
следует, что числитель формулы (16.3) равен единице |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
(e j ×ek ) (e j ×ek ) = (e j |
e j ) (ek ek ) −(e j |
ek ) (ek e j ) =1 1−0 0 =1 |
|
(17.3) |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
||
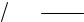
а тогда знаменатель должен быть равен тоже единице, так как ei ei =1 , а, кроме того,
легко видеть, что em ×en = el , e m ×e n = e l , откуда получается, что
V V 1 |
=1, ч.т.д. |
(18.3) |
1 |
|
|
Определение связи между проекциями вектора во взаимных базисах
Задача 1.3 Пусть заданы три произвольных некомпланарных вектора b1, b2 , b3, которые выбираются в виде системы координат. Требуется разложить по ним вектор b. Задача сводится к определению компонентов b1, b2, b3 из системы трёх скалярных уравнений, полученных проектированием выражения
b = b1b1 + b2b2 + b3b3
на оси этого базиса.
Решение. Для решения этой задачи нужно использовать два взаимных базиса, чтобы получить связь между проекциями векторов во взаимных базисах. Для определения
проекций bk из векторного уравнения
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
b = b1b1 + b2b2 + b3b3 = ∑bibi |
, |
|
|
(19.3) |
||||||||
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
где b1,b2 , b3 - некомпланарные векторы, |
умножим вектор b на bk - |
вектор взаимного |
|||||||||||
базиса. Тогда получим (см. формулу (4.3)) |
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
b bk |
= ∑bibi bk |
= bk |
|
|
|
|
(20.3) |
|||||
так как |
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
если |
i ≠ k |
|
|
|
|
|
||||
|
bi bk |
|
. |
|
|
|
|
||||||
|
= |
|
если |
i = k |
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|||||
Отсюда получаются искомые проекции в виде |
|
|
|
|
|
|
|
||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
bk = ∑bibi bk |
|
|
|
|
|
|
|
|
(21.3) |
|||
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 7.3 Из формул (20.3) и (12.3) получается |
|
|
|
|
|
||||||||
|
b1 = b b1 = |
|
b ( b2 ×b3 ) |
|
|
|
|
|
(22.3) |
||||
|
|
b1 (b2 ×b3 ) |
|
|
b |
|
|||||||
|
|
|
|
|
|
|
|
||||||
Замечание |
8.3. Здесь интересно |
|
равенство |
|
b b1 = |
которое |
получается из |
||||||
|
|
|
|||||||||||
|
|
|
b |
|
|
|
|
|
|
b1 |
|
||
b b1 b1 = b 1 = b или из b b1 b1 = |
= b . |
|
|
|
|
|
|
|
|||||
Задача 2.3 |
|
b1 |
b1 |
|
|
|
|
|
|
|
|
|
|
Требуется найти вектор А, удовлетворяющий трём уравнениям |
|||||||||||||
|
A a1 = m1; |
|
A a2 = m2 ; |
|
A a3 = m3 , |
(23.3) |
|||||||
где заданы некомпланарные векторы a1,a2 ,a3 , а |
m1,m2 ,m3 - скаляры. |
|
|||||||||||
Решение. Для решения данной задачи нужно выразить вектор А через компоненты
взаимного базиса в виде
A = m1a1 + m2a2 + m3a3 |
(24.3) |
Для доказательства того, что (24.3) является решением поставленной задачи, умножим это равенство на a1 . Тогда получается, что
A a1 = m1a1 a1 + m2a2 a1 + m3a3 a1 = m1a1 a1 = m1, |
(25.3) |
15
что и отвечает условиям задачи (2.3).
Векторы a1,a2 ,a3 определяются по формулам (12.3).
Доказательство единственности решения (24.3) выполняется от противного. Допустим, что есть решение, отличное от (23.3) в виде
A' a1 = m1; A' a2 = m2 ; A' a3 = m3 |
(26.3) |
Вычитая из (23.3) выражение (26.3), получим |
|
( A - A' ) a1 = m1 - m1 = 0, |
|
( A - A' ) a2 = m2 - m2 = 0, |
(27.3) |
( A - A' ) a3 = m3 - m3 = 0. |
|
Вектор A - A' перпендикулярен всем некомпланарным векторам a1,a2 ,a3 (так как
скалярное произведение равно нулю, если векторы взаимно перпендикулярны) и может быть только нуль – вектором, откуда A = A' , и значит, решение единственно, ч.т.д. Отсюда следует, что решением поставленной задачи 2.3 является выражение (24.3)
Замечание 9.3 Эти задачи демонстрируют каким образом использование взаимного базиса упрощает решение геометрических задач.
§ 4. Переход от одного ортонормированного базиса к другому
Замечание 1.4 Переход от одного базиса к другому является ключевой задачей тензорного исчисления (эта задача была сформулирована выше в § 2 в виде первой основной задачи).
Пусть требуется записать в знаках и индексах тензорного исчисления систему перехода от одного ортонормированного базиса к другому. Для этого базис e'1 ,e'2 ,e'3
нужно выразить через базис e1 ,e2 ,e3 , то есть, получить систему
e' |
|
= a e |
+ a |
|
e |
2 |
+ a |
|
e |
3 |
|
|
|
|||
1 |
1'1 |
1 |
1'2 |
|
|
1'3 |
|
|
|
|
||||||
e'2 = a2'1e1 + a2'2e2 + a2'3e3 |
|
(1.4) |
||||||||||||||
e' |
3 |
= a |
e |
+ a |
3'2 |
e |
2 |
+ a |
3'3 |
e |
3 |
|
|
|||
|
3'1 |
1 |
|
|
|
|
|
|
|
|||||||
Это можно записать в виде произведения матриц
e' |
|
a |
a |
a |
|
e |
|
|
1 |
|
1'1 |
1'2 |
1'3 |
|
1 |
|
|
e'2 |
|
= a2'1 |
a2'2 |
a2'3 |
|
e2 |
|
= |
|
|
|
a3'2 |
|
|
|
|
|
e'3 |
|
a3'1 |
a3'3 |
e3 |
|
|
||
e1
ai'i e2 (1’.4)
e3
В сокращённой записи эта система выглядит так: |
|
e'i = ai'iei (i,i'=1,2,3) , |
(2.4) |
где
|
a |
a |
|
1'1 |
1'2 |
ai'i |
= a2'1 |
a2'2 |
|
|
a3'2 |
|
a3'1 |
a |
|
|
1'3 |
|
|
a2'3 |
|
(3.4) |
|
|
|
a3'3 |
|
|
матрица коэффициентов, которая является тензором второго ранга, Базисные векторы записываются тоже в матричном виде
e'1 e'i = e'2 ;
e'3
e1
ei = e2 (4.4)
e3
Каждое из равенств (1.4) умножим скалярно на каждый из векторов ei . При этом с учётом того, что e'i ei =1 1 =1, и формулы (3.4) можно написать
16
e'i ei = |
|
e'i |
|
|
|
ei |
|
cos(e'i ,ei ) = cos(e'i ,ei ) = ai ' i |
(5.4) |
|
|
|
|
так как векторы e'i ,ei в данном случае элементы матрицы (3.4) равны
a |
=cos(e' |
,e |
i |
) |
при (i ',i =1,2,3) |
(6.4) |
i'i |
i |
|
|
|
|
|
Если выразить e1 ,e2 , e3 через e'1 , e'2 |
, e'3 , то получим |
|
||||
|
e = a e' |
+ a e' |
+a e' |
|
|
|
|
|||||||||||||||
|
1 |
|
|
11' |
1 |
12' |
|
2 |
|
13' |
|
3 |
|
|
|
|||||||
|
e |
2 |
= a |
|
e' |
+ a |
22' |
e' |
|
+a |
23' |
e' |
|
|
|
|||||||
|
|
|
|
|
21' |
1 |
|
|
2 |
|
|
|
3 |
|
|
|||||||
|
e |
3 |
= a |
31' |
e' |
+ a |
32' |
e' |
|
+ a |
33' |
e' |
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
3 |
|
|
|||||||
|
e |
|
|
|
a |
|
|
a |
|
|
|
a |
|
|
|
|
e' |
|
||||
|
|
1 |
|
|
|
11' |
|
12' |
|
13' |
|
|
|
1 |
|
|||||||
или |
e2 |
|
= a21' |
|
a22' |
|
a23' |
|
|
e'2 |
|
|||||||||||
|
e |
|
|
|
a |
|
|
a |
|
|
|
a |
|
|
|
|
e' |
|
||||
|
|
|
3 |
|
|
31' |
|
32' |
|
33' |
|
|
|
3 |
|
|||||||
или сокращённо
(7.4)
(7’.4)
ei = ai i'e'i |
(8.4) |
Умножая каждое равенство системы (7.4) на каждый из новых векторов e'1 , e'2 , e'3 ,
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ei e'i = |
|
ei |
|
|
|
e'i |
|
cos(ei ,e'i ) = ai i' |
(9.4) |
||||||
|
|
|
|
||||||||||||
или |
|
|
|
e' |
|
|
|
|
|
|
,e' |
|
|
||
a |
i i ' |
= e |
i |
|
= cos(e |
) |
(9’.4) |
||||||||
|
|
|
|
i |
|
|
|
|
|
i |
i |
|
|
||
Сравнивая (2.4) и (8.4), легко видеть, что матрицы преобразований равны, так как косинус
– чётная функция. Отсюда получается важное равенство элементов матриц
коэффициентов систем
ai'i = ai i' |
(10.4) |
Замечание 1.4 Следует помнить, что формула (10.4) справедлива для
ортонормированных базисов.
Числа ai 'i матрицы (3.4) являются элементами матрицы перехода А
a |
a |
a |
|
|
1'1 |
1'2 |
1'3 |
|
|
A = a2'1 |
a2'2 |
a2'3 |
|
(11.4) |
|
a3'2 |
a3'3 |
|
|
a3'1 |
|
|
от старого базиса e1 ,e2 ,e3 к новому e'1 , e'2 , e'3 . Это матрица третьего порядка. Матрица перехода от нового базиса к старому обозначается в виде А-1
|
a |
a |
A−1 |
11' |
12' |
= a21' |
a22' |
|
|
|
a32' |
|
a31' |
a |
|
|
13' |
|
|
a23' |
|
(12.4) |
|
|
|
a33' |
|
|
Сокращённая запись (11.4) и (12.4), как и (3.4), имеет вид
A = ai'i и A−1 = ai i' |
(13.4) |
Докажем, что матрица (12.4) действительно является обратной по отношению к матрице (11.4). Для этого подставим векторы новой системы (1’.4) в выражение (7’.4) Тогда мы получим
17
e |
|
|
a |
|
1 |
|
|
|
11' |
e2 |
|
= a21' |
||
|
|
|
|
|
e3 |
|
|
a31' |
|
a |
|
|
a |
|
|
11' |
|
12' |
|
= a21' |
|
a22' |
||
|
|
|
|
a32' |
a31' |
|
|||
a12' a22' a32' a13' a23' a33'
a |
|
|
|
e' |
|
|
||
|
13' |
|
|
|
1 |
|
|
|
|
a23' |
|
e'2 |
|
= |
|||
|
|
|
|
|
|
|
|
|
|
a33' |
|
e'3 |
|
|
|||
|
|
a |
|
|
|
a |
|
a |
|
|
1'1 |
|
|
1'2 |
1'3 |
||
|
|
a2'1 |
|
a2'2 |
a2'3 |
|||
|
|
|
|
|
|
a3'2 |
a3'3 |
|
|
|
a3'1 |
|
|||||
(14.4)
e1e2e3
Вспомним, во-первых, что две матрицы равны в том случае, когда на одинаковых местах стоят равные элементы, во-вторых, что произведение любой матрицы на единичную матрицу равно исходной матрице A E = A и E A = A. Следовательно, для того, чтобы левая часть равенства (14.4) равнялась правой части, необходимо и
достаточно, чтобы произведение матриц A A−1 равнялось единичной матрице A A−1 = E . Итак, это равенство может выполняться только, если
|
a |
a |
A A−1 |
11' |
12' |
= a21' |
a22' |
|
|
|
a32' |
|
a31' |
a13' a23' a33'
a1'1a2'1a3'1
a1'2 a2'2 a3'2
a1'3 a2'3 = a3'3
1 |
0 |
0 |
||
|
0 |
1 |
0 |
|
E = |
|
|||
|
0 |
0 |
|
|
|
1 |
|||
Перемножение прямой и обратной матриц даёт ряд важных зависимостей
a |
|
|
a |
|
|
a |
|
|
|
a |
|
|
|
|
a |
|
|
a |
|
|
a a |
|
|
+ a a |
21' |
+ a a |
31' |
|
|||||||||||||||||||||||
1'1 |
|
1'2 |
|
1'3 |
|
|
|
|
11' |
|
|
12' |
|
13' |
|
|
1'1 |
|
11' |
|
|
|
1'2 |
|
|
|
1'3 |
|
|
||||||||||||||||||||||
a2'1 |
|
a2'2 |
|
a2'3 |
|
a21' |
|
|
a22' |
|
a23' |
|
= a2'1a11' |
+ a2'2 a21' |
+ a2'3a31' |
|
|||||||||||||||||||||||||||||||||||
a |
3'1 |
a |
3'2 |
|
a |
3'3 |
a |
31' |
|
|
a |
32' |
|
a |
33' |
|
a |
3'1 |
a |
|
+ a |
3'2 |
a |
21' |
+ a |
3'3 |
a |
31' |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11' |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
a a |
|
|
+ a a |
22' |
|
+ a a |
32' |
|
a a |
+ a a |
23' |
+ a a |
33' |
|
|
1 0 0 |
||||||||||||||||||||||||||||||||||
|
1'1 |
12' |
|
1'2 |
|
|
|
|
1'3 |
|
|
1'1 13' |
|
1'2 |
|
|
|
|
1'3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
a2'1a12' + a2'2 a22' + a2'3a32' |
a2'1a13' |
+ a2'2 a23' |
|
+ a2'3a33' |
|
= |
0 |
|
1 0 |
|
||||||||||||||||||||||||||||||||||||||||
|
a |
a |
|
|
+ a |
3'2 |
a |
22' |
+ a |
3'3 |
a |
32' |
a |
|
a |
|
+ a |
3'2 |
a |
23' |
+ a |
3'3 |
a |
33' |
|
|
0 0 1 |
||||||||||||||||||||||||
|
|
3'1 |
12' |
|
|
|
|
|
|
|
|
|
|
3'1 13' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Отсюда в силу справедливости формулы (10.4) получаются очевидные равенства |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1'1a11' + a1'2a21' + a1'3a31' =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2'1a11' + a2'2a21' + a2'3a31' = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(15.4) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3'1a11' + a3'2a21' + a3'3a31' = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1'1a12' + a1'2 a22' + a1'3a32' |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2'1a12' + a2'2 a22' |
+ a2'3a32' |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(16.4) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3'1a12' + a3'2 a22' + a3'3a32' |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1'1a13' + a1'2 a23' |
+ a1'3a33' |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2'1a13' + a2'2 a23' |
+ a2'3a33' |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(17.4) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3'1a13' + a3'2 a23' |
+ a3'3a33' |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
например, (17.4) коротко можно записать в тензорном |
|
|
|
|
виде |
(см. соглашение о |
|||||||||||||||||||||||||||||||||||||||||||||
суммировании в § 6 этой главы): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
ak' j a jk' = ak'1a1k' + ak'2a2k' + ak'3a3k' |
=1 |
|
|
|
k'=1,2,3 |
|
(18.4) |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ai' j a jk' = ai'1a1k' + ai'a2k' + ai'3a3k' = 0 |
|
|
i'≠ k |
' |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
или |
|
|
|
ai'k a k |
j' = ak i' a j'k |
=δi' j' |
|
(k =1,2,3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(19.4) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
a k'i a j k' |
= ai k' |
ak' j |
=δi j |
|
(k'=1,2,3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(20.4) |
|||||||||||||||||||||||||||
где δi' |
j' и δi j - символы (дельта) Кронекера. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
18

Замечание 2.4 Дельту Кронекера иногда называют оператором замены, потому что она даёт следующие преобразования
δi jb j =δi1b1 +δi 2b2 +δi 3b3 = bi |
(21.4) |
или |
|
δi j Ai k =δ1 j A1k +δ2 j A2 k +δ3 j A3 k = Aj k |
(22.4) |
Замечание 3.4 Благодаря этим свойствам дельта Кронекера является аналогом
единичного тензора второго ранга.
Пример 1.4 Пусть заданы углы между направлениями координат системы со штрихами и системы без штрихов в следующей таблице:
|
x1 |
x2 |
x3 |
' |
135о |
60о |
120о |
x1 |
|
|
|
' |
90о |
45о |
45о |
x2 |
|
|
|
' |
45о |
60о |
120о |
x3 |
|
|
|
Определить коэффициенты преобразования aij и показать, что выполнены условия
ортогональности.
Решение. Коэффициенты aij являются направляющими косинусами и могут быть вычислены в соответствии с данной таблицей углов
|
|
|
− |
2 2 |
1 2 |
−1 2 |
|
|
|
|
|
|
|
|
|
a |
ij |
= |
|
0 |
2 2 |
2 2 |
|
|
|
|
2 2 1 2 |
−1 2 |
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Условия ортогональности aij aik = δ jk требуют, чтобы выполнялись следующие условия:
1) при j = k =1 должно быть aij aij = a11a11 + a21a21 + a31a31 =1. Левая часть представляет собой сумму квадратов элементов первого столбца.
2)при j = 2, k = 3 должно быть выполнено равенство a12a13 + a22a23 + a32a33 = 0 . Левая часть представляет собой сумму произведений соответствующих элементов второго и третьего столбца.
3)сумма произведений соответствующих элементов любых двух столбцов должна быть равна нулю.
4)сумма квадратов элементов любого столбца должна быть равна единице.
5)если условие ортогональности написано в виде a ji aki = δ jk , то вместо столбцов
перемножаются строки
Проверка суммы квадратов столбцов.
(−  2 2)2 + 02 + (
2 2)2 + 02 + ( 2 2)2 = 2 4 + 0 + 2 4 =1 (1 2)2 + (
2 2)2 = 2 4 + 0 + 2 4 =1 (1 2)2 + ( 2 2)2 + (1
2 2)2 + (1 2)2 =1 4 + 2 4 +1 4 =1
2)2 =1 4 + 2 4 +1 4 =1
(−1 2)2 + ( 2 2)2 + (−1
2 2)2 + (−1 2)2 =1 4 + 2 4 +1 4 =1
2)2 =1 4 + 2 4 +1 4 =1
Проверка условия 2).
1 2(−1 2)+  2 2
2 2  2 2 +1 2 (−1 2)= −1
2 2 +1 2 (−1 2)= −1 4 + 2
4 + 2 4 −1
4 −1 4 =0
4 =0
Проверка суммы квадратов строк.
19
|
|
|
|
|
(− 2 2)2 + (1 2)2 + (−1 2)2 = 2 4 +1 4 +1 4 =1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
02 + ( 2 2)2 + ( 2 2)2 = 0 + 2 4 + 2 4 =1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
( 2 2)2 + (1 2)2 + (−1 2)2 = 2 4 +1 4 +1 4 =1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Проверка суммы произведений соответствующих элементов двух параллельных |
|||||||||||||||||||||||||||||||
строк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) (2) |
− |
|
2 2 0 +1 2 |
2 2 −1 2 |
2 2 = 0 + |
2 4 − |
2 4 = 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
(1) (3) |
− |
|
2 2 |
|
2 2 +1 2 1 2 +1 2 1 2 = −2 4 +1 4 +1 4 = 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
(3) (2) |
− |
|
2 2 0 +1 2 |
2 2 −1 2 |
2 2 = 0 + |
2 4 − |
2 4 = 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
Проверка произведений соответствующих элементов двух параллельных столбцов |
|||||||||||||||||||||||||||||||
(1) (2) |
− |
|
2 2 1 2 + 0 |
2 2 + |
2 2 1 2 = − |
|
2 4 + 0 + 2 4 = 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
(1) (3) |
− |
|
2 2 (−1 2)+ 0 |
2 2 + |
2 2 (−1 2)= |
2 4 + 0 − |
2 4 = 0 |
|
|
|
|
|
|
|
|
||||||||||||||||
(2) (3) |
1 2 (−1 2)+ |
2 2 |
2 2 +1 2 (−1 2)= −1 4 + 2 4 −1 4 = 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Ответ: все условия ортогональности в данной таблице выполняются. |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
§ 5. Ковариантные и контравариантные компоненты |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 1.5 В векторной алгебре компонентами |
||||||||||||||||||
|
е2 |
|
|
|
x 2 |
|
|
|
|
|
|
вектора называют его составляющие, которые являются |
|||||||||||||||||||
a2e2 D |
|
|
|
|
|
|
|
|
|
|
|
векторами. В отличие от векторной алгебры, в |
|||||||||||||||||||
|
|
|
е2 |
|
|
|
|
|
|
|
тензорном |
исчислении |
компонентами |
называют |
|||||||||||||||||
|
a2e |
2 |
С |
a |
|
|
|
|
|
проекции, которые являются скалярами a1 , a2 |
и a1 , a2 . |
||||||||||||||||||||
|
E |
|
|
|
|
|
|
|
Рассмотрим связь между реперами и кореперами не в |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
пространстве, как выше, а на плоскости. |
|
|
|
|
||||||||||||||
|
|
|
1F |
А |
|
|
е1 |
|
x1 |
|
|
|
На рисунке 1.5 показан вектор а в основном базисе |
||||||||||||||||||
О |
|
|
|
|
|
|
e1 ,e2 |
(реперы) и во взаимном базисе e1 ,e2 |
(кореперы). |
||||||||||||||||||||||
|
|
|
a |
e1 |
В |
|
|
|
|
|
|
Векторы взаимного базиса перпендикулярны векторам |
|||||||||||||||||||
|
|
|
|
a1e1 |
|
|
|
e1 |
|
|
основного |
|
базиса. |
На |
рисунке |
1.5 |
показаны также |
||||||||||||||
|
|
|
|
|
|
|
|
|
компоненты a1 , a2 |
вектора в основном базисе |
и a1 , a2 |
||||||||||||||||||||
Рис. 1.5 |
Реперы и кореперы |
|
|
во взаимном базисе. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составляющие |
|
е |
2 |
a2 |
|
|
|
|
|||||||
вектора |
|
|
по |
|
|
|
основному |
|
|
|
базису |
|
равны |
|
|
е2 |
|
|
|||||||||||||
|
1 |
, OE = a |
2 |
e2 |
, |
а |
по |
|
взаимному |
|
базису |
- |
a e2 |
C |
|
e |
2 |
|
|
|
|
||||||||||
OF = a e1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
OB = a1e1 , OD = a2e2 .. |
|
|
|
|
|
a1, a2 называются |
a 2 |
|
|
|
|
a2 e2 |
|
a |
|
|
|||||||||||||||
Определение |
|
|
1.5 |
|
Числа |
|
|
e 2 |
|
|
|
|
|
a1 |
|
|
|||||||||||||||
контравариантными компонентами вектора а. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Определение |
|
2.5 |
|
Числа |
|
a1, a2 |
|
называются |
O |
|
a |
1 |
e1 D |
|
e1 |
|
е1 |
||||||||||||||
ковариантными компонентами вектора а. |
|
|
|
|
|
|
|
|
A |
|
|
||||||||||||||||||||
|
|
|
|
|
|
a1 |
|
|
|
|
|
||||||||||||||||||||
Определение |
3.5 |
|
Контравариантные |
|
компоненты |
|
|
E |
|
|
|
||||||||||||||||||||
a1, a2 (индекс вверху) |
можно найти из составляющих |
|
e1 |
|
|
B |
|
|
|||||||||||||||||||||||
a1 e , a2 e |
2 |
по направлению основного базиса, а |
также |
|
|
|
|
|
a1 e1 |
|
e1 |
||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.5 Вектор а в основном и |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
a2 |
|
|
|
||||||||||||
из проекций на оси взаимного базиса |
|
|
|
|
взаимном базисе |
|
|||||||||||||||||||||||||
|
1 , |
e |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
