Мощность генераторов

P_Г = E₁ ·I₁-E^’₂·I₂-E₃ ·I₃= 27·0,266 - 21· (-0,357) - 9· (-0,151)=

=16,037 Вт.

Относительная погрешность составляет

.

5. Построим потенциальную диаграмму для первого контура. Примем φ_b=0, тогда

φ₁= φ_b+E₁=27 B;

φ_a= φ₁-I₁ R₁=27-0,266·100=0,4 B;

φ₂= φ_a+E¹₂=0,4+21=21,4 B;

φ_b= φ₂+I₂R₂=21,4-0,357·60= -0,02 B≈ 0.

Потенциальная диаграмма имеет вид

Рис. 2.1-3

6. Представим всю цепь относительно сопротивления R₅ активным двухполюсником и заменим его эквивалентным генератором

Рис.2.1-4

Рис. 2.1-5

ЭДС эквивалентного генератора Е_г определяется как напряжение холостого хода на зажимах разомкнутой пятой ветви U_{cb xx}:

Сопротивление эквивалентного генератора R_г определяется как входное сопротивление двухполюсника при закороченных источниках ЭДС.

Рис. 2.1-6

Ток и мощность в сопротивлении R₅

Графики функций I₅=f(R₅) и P₅=f(R₅) в диапазоне 0-200 Ом :

Рис. 2.1-7

Обращаем внимание на то, что при R₅=75 Ом, ток I₅=0,06 A, что совпадает с рассчитанным ранее, а максимум мощности достигается при R₅=22 Ом, т.е. при R₅= R_г.

Пример 2. Электрическая цепь синусоидального тока

(основные теоретические сведения приведены в п 1.2)

Д ано:

Рис. 2.2-1

E_m1=120 B, ₁= -90^, E_m2=70 B, ₂=120^, R₁=30 Ом, R₂=20 Ом

L₁=40 мГн, L₂=25 мГн, C=20 мкФ, f=200 Гц.

Решение:

Примем направление токов, как показано на схеме, обход контуров – по часовой стрелке. Система уравнений в дифференциальной форме:

Система уравнений в символической форме:

1. Определим комплексы ЭДС и сопротивлений в ветвях:

Рис.2.2-2

2. Определим токи в ветвях методом двух узлов:

Преобразуем числитель:

Преобразуем знаменатель:

Комплексы токов:

3. Активная мощность потребителей:

Реактивная мощность потребителей:

Комплекс полной мощности генераторов:

Баланс выполняется, погрешность менее 1%.

4.Рассчитаем потенциалы точек в исходной схеме. Примем  _b=0.

Проверка:

Строим топографическую диаграмму напряжений. Масштаб напряжений нанесен непосредственно на осях комплексной плоскости. Заметим, что вектор, соответствующий разности потенциалов, направлен в сторону точки, потенциал которой указывается первым. Например, вектор напряжения

соединяет точки а и с на топографической диаграмме и направлен в сторону точки с.

Рис. 2.2-3

Отложим комплексы токов, выбрав соответствующий масштаб. Обратим внимание на выполнение 1-го закона Кирхгофа.

4.Запишем выражения для мгновенных значений тока i₁ и напряжения U_ab:

Рис. 2.2-4

Пример 3. Трехфазная электрическая цепь при соединении нагрузки «звездой» (основные теоретические сведения приведены в п.1.3)

Дано: U_ф =660 В; R=60 Ом; Х_L=100 Ом; X_C=70 Ом.

Неполнофазный режим: Z_A=0.

Рис. 2.3-1

Решение:

Фазные ЭДС генератора:

Комплексные сопротивления фаз нагрузки:

Напряжение смещения нейтрали:

Числитель:

Знаменатель:

Напряжения на фазах нагрузки:

Токи в фазах нагрузки:

Проверим выполнение I закона Кирхгофа:

Определим мощности:

П остроим векторную диаграмму токов и напряжений.

Рис.2.3-2

Напомним, что при построении векторных диаграмм для трехфазной цепи вещественную ось комплексной плоскости принято направлять вверх. Масштаб: для напряжения – одно деление = 100 В, для тока – одно деление = 5 А.

Рассчитаем цепь при замыкании накоротко фазы А

(рис. 2.3-3). В этом случае напряжение смещения нейтрали равно ЭДС фазы А:

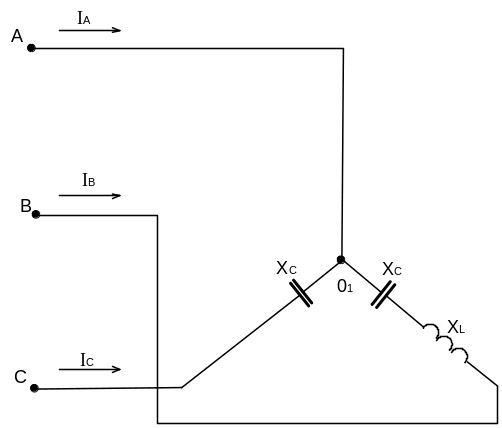
Рис.2.3-3

Напряжение на фазе А нагрузки Напряжение на других фазах:

Токи в фазах:

Векторная диаграмма неполнофазного режима показана на рис. 2.3-4 (масштаб тот же, что и на диаграмме рис.2.3-2):

Рис. 2.3-4

П ример 4. Трехфазная электрическая цепь при соединении нагрузки «треугольником» (основные теоретические сведения приведены в п.1.3)

Дано:

U_л =220 В;

R=40 Ом;

Х_L=50 Ом;

X_C=60 Ом.

Неполнофазный режим: Z_A=.

Рис. 2.4-1

Решение:

Линейные напряжения:

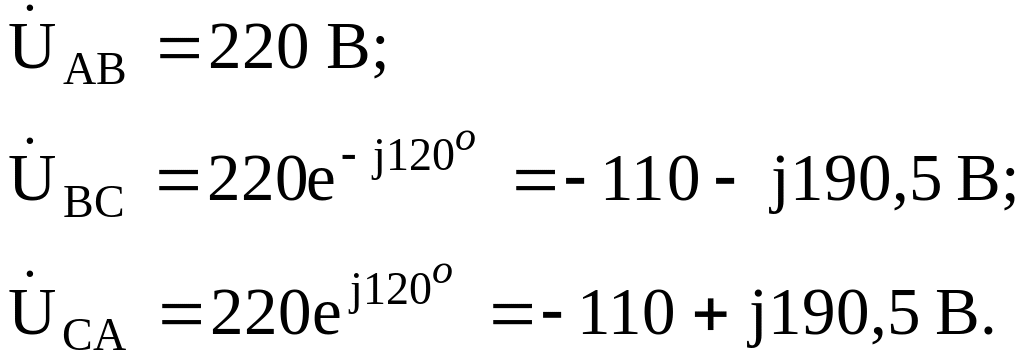
Комплексные сопротивления фаз нагрузки:

Токи в фазах нагрузки:

Определим токи в линиях:

Проверим выполнение I закона Кирхгофа:

Определим мощности:

Рассчитаем цепь при обрыве линии А (рис. 2.4-2)

При обрыве линии А ток .

Найдем ток :

Рис.2.4-2

Токи в фазах:

Проверка: .

Напряжения в фазах нагрузки:

Проверка:

Векторные диаграммы токов и напряжений неполнофазного режима .

Рис. 2.4-3 (1 деление – 50 В)

Рис. 2.4-4 (1 деление – 2 А)

Пример 5. Расчет электрической цепи при периодическом несинусоидальном входном воздействии (необходимые теоретические сведения приведены в п.1.4)

Рис. 2.5-1

Рис. 2.5-2

Дано: U_m=20 B; T=0,5 мс; R=10 Ом; L₁=1 мГн;

L₂=0,5 мГн; C₁=4 мкФ; C₂=1,4 мкФ.

Определить

Решение: Определим характеристики входного напряжения:

А мплитудный и фазовый спектры имеют вид:

Рис. 2.5-3

Определим U_L2 для каждой из составляющих входного сигнала.

Постоянная составляющая U₁=10 В. При воздействии постоянной составляющей токи в цепи отсутствуют, т. к. конденсатор представляет бесконечно большое сопротивление. Поэтому U_L2=0.

Первая гармоника:

В качестве модуля комплексов удобно использовать амплитудные значения.

Реактивные сопротивления:

Входное сопротивление:

Определяем комплекс напряжения :

Мгновенное значение:

Третья гармоника:

Реактивные сопротивления:

В последовательном контуре L₂-C₂ на третьей гармонике резонанс напряжений. Сопротивление последовательного контура при резонансе равно нулю. Поэтому

Мгновенное значение искомой величины:

Действующее значение:

Г

u, B

3

1

2

t



-/2

/2

3/2

0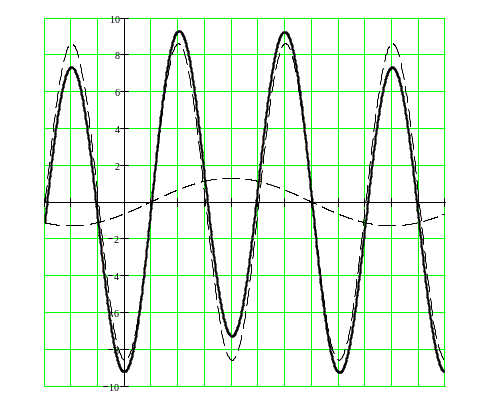

рафик искомой величины показан на рис. 2.5-4.

Рис. 2.5-4 (1 - ; 2 - ; 3 - )

Пример 6. Расчет апериодического переходного процесса (основные теоретические сведения приведены в п.1.5)

Рис. 2.6-1

Дано: E=120 B; L=400 мГн; R₁=25 Ом; R₂=15 Ом; C=80 мкФ.

Определить i₁(t).

Решение:

1. Классический метод

Первоначально удобно решать задачу относительно напряжения на конденсаторе U_C(t):

.

Принужденная составляющая напряжения U_{C пр} – это установившееся

значение напряжения после завершения переходного процесса:

Свободная составляющая U_{C св} – это общее решение однородного дифференциального уравнения второго порядка, которое записывается в виде

,

где p₁, p₂ – корни характеристического уравнения;

A₁, A₂ – постоянные интегрирования.

Для определения корней характеристического уравнения запишем выражение входного сопротивления для послекоммутационной схемы на переменном токе. Заменив jω на p, приравняем к нулю полученное выражение. Заметим, что входное сопротивление может быть записано относительно любой ветви. В нашем случае это удобно сделать для ветви с индуктивностью:

Подставим численные данные и решим уравнение :

Подставим найденные величины в исходное уравнение:

.

Продифференцируем обе части по времени:

Для определения постоянных интегрирования необходимо определить значение искомой функции и ее первой производной в начальный период времени. Полагая t=0₊ , получим два уравнения для определения А₁и А₂:

Определим ток в катушке и напряжение на конденсаторе в докоммутационной схеме:

В соответствии с законом коммутации

Ток в конденсаторе откуда

Запишем уравнения по законам Кирхгофа для начального момента времени:

Из второго уравнения

.

Из первого уравнения

Подставим найденные значения в систему для определения постоянных интегрирования:

Искомая функция имеет вид

Ток i₁(t) определим из уравнения по закону Кирхгофа:

2. Операторный метод.

О ператорная схема замещения имеет вид:

Рис. 2.6-2

Определим изображение тока I₁(p) методом контурных токов.

Главный определитель системы

Вспомогательный определитель для тока I₁₁(p)

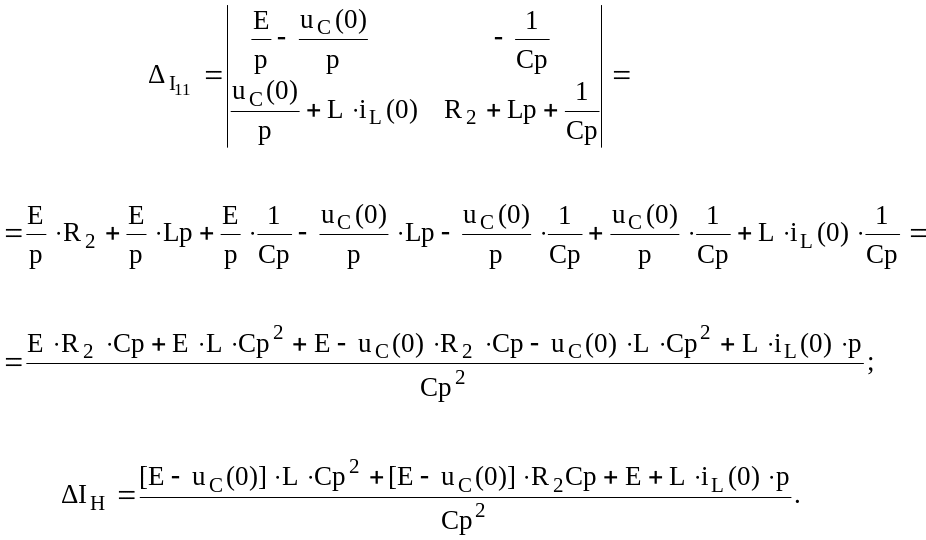
Так как U_C(0)=Е, то

Изображение функции тока:

Подставим численные значения:

Для перехода к функции времени используем формулу разложения:

Определим производную знаменателя:

Определим значение числителя и производной знаменателя для всех корней:

.

Получаем искомую функцию:

3. График функции показан на рис. 2.6-3

Постоянные времени экспонент:

Рис. 2.6-3

Пример 7. Периодический переходный процесс в цепи второго порядка (основные теоретические сведения приведены в п.1.5)

Рис. 2.7-1

Дано:

E=72 B; R₁=100 Ом; R₂=500 Ом; L=50 мГн; C=0,5 мкФ.

Определить u_L(t)

Решение:

1. Классический метод.

Определим переходную функцию тока в индуктивности i(t).

В принужденном режиме все токи схемы равны нулю, так как сопротивление конденсатора бесконечно велико:

Запишем входное сопротивление цепи и определим корни характеристического уравнения:

Подставим числовые значения:

Комплексно-сопряженные корни характеристического уравнения говорят о периодическом характере переходного процесса. При этом

где - коэффициент затухания;

- циклическая частота свободных колебаний.

Определим постоянные интегрирования:

В начальный момент времени

Независимые начальные условия:

Для определения составим уравнения по законам Кирхгофа для первого момента времени после коммутации:

Подставим ток во второе уравнение и решим относительно :

Функции тока и напряжения на индуктивности связаны следующим соотношением:

В начальный момент времени

Отсюда

Система для определения постоянных интегрирования:

Подставим найденные значения в выражение для тока и преобразуем его:

Правую часть умножим и разделим на 2:

В соответствии с формулами Эйлера выражение в квадратных скобках равно :

Для определения функции напряжения на индуктивности нужно взять производную функции тока и умножить на L. Используем правило дифференцирования произведения:

Чтобы свернуть выражение в скобках, воспользуемся комплексным методом:

Рис. 2.7-2

2.Операторный метод.

Н ачальные условия в схеме нулевые, поэтому операторные ЭДС отсутствуют.

Рис. 2.7-3

Воспользуемся методом двух узлов:

Подставим числовые значения:

Корни уравнения M(p)=0:

Производная знаменателя:

Переходим от изображения к функции времени:

Умножим и разделим дробь на 2 и воспользуемся формулой Эйлера:

Для построения графика функции определим период гармонических колебаний и постоянную времени экспоненциальной огибающей амплитуды

Этапы построения графика:

кривая 1 - синусоида заданной частоты с начальной фазой сдвига , с неизменной амплитудой;

кривые 2 и 3 - огибающие экспоненты;

кривая 4 - окончательная кривая , где учтены начальные условия и уменьшение амплитуды в соответствии с огибающей.

Рис. 2.7-4

Пример 8. Расчет нелинейной электрической цепи методом эквивалентных синусоид (основные теоретические сведения приведены в п.1.6)

Дано:

R₁=12 Ом;

R₂=5 Ом;

X_C=25 Ом.

Рис. 2.8-1

Вольт-амперная характеристика нелинейной индуктивности по действующим значениям напряжения и тока приведена на графике (рис.2.8-2).

Рис.2.8-2

Решение:

1. Вольт-амперная характеристика цепи.

Считая токи и напряжения синусоидальными функциями, используем комплексный метод расчета. Задаваясь рядом значений тока I₂ и считая его начальную фазу нулевой, определим комплексы входных тока и напряжения.

Данный режим соответствует резонансу, так как фаза входного тока равна фазе входного напряжения 76^о ≈ 78^о.

Вольтамперная характеристика цепи

Рис. 2.8-6

При питании цепи от источника с большим внутренним сопротивлением (источника тока) в цепи будет наблюдаться триггерный эффект (скачкообразные изменения напряжения). При изменении действующего значения входного напряжения ток будет плавно изменяться, при этом триггерного эффекта не будет.

Отметим также, что до резонанса ток опережал по фазе напряжение, то есть цепь имела емкостный характер. После резонанса ток отстает по фазе от напряжения, следовательно, цепь имеет индуктивный характер.

Пример 9. Расчет электрической цепи с распределенными параметрами (основные теоретические сведения приведены в п.1.8)

Дано:

Генератор соединен с приемником длинной линией. Напряжение и частота генератора

U₁= 220 B; f= 8800 Гц.

Параметры линии:

l=21 км; R₀=185 Ом/км; G₀=16,510^-6 См/км;

L₀= 6,2 мГн/км; C₀=7,1 нФ/км.

Сопротивление нагрузки

Z_н= 110+j260 Ом.

Решение:

1. Рассчитаем волновые параметры линии.

Циклическая частота генератора

Продольное сопротивление линии

Поперечная проводимость линии

Постоянная распространения волны

Коэффициент затухания

Коэффициент фазы

Волновое сопротивление линии

Фазовая скорость

Длина волны

2. Определим токи, напряжения и мощности в начале и в конце линии.

Уравнения установившегося синусоидального режима в линии:

где - комплексы напряжения и тока в конце линии;

- комплексы напряжения и тока в точке, находящейся на расстоянии y от конца линии.

Полагая y=l, получим

где - напряжение и ток в начале линии.

Аргумент гиперболических функций

Гиперболические косинус и синус комплексного аргумента могут быть вычислены по следующим формулам:

Гиперболические функции вещественного аргумента могут быть получены с помощью таблиц либо определены по формулам:

При вычислении круговых косинуса и синуса необходимо помнить, что аргумент задан в радианах. Если потребуется перевести его в градусы, то можно воспользоваться соотношением

Для и окончательно получаем

Напряжение и ток в конце линии связаны соотношением

Ток в конце линии получим из первого уравнения режима:

Напряжение в конце линии

Ток в начале линии - из второго уравнения:

Активная мощность в начале и в конце линии

Вт

К.п.д. линии

%.

3. Рассчитаем линию без потерь R_ = G_ = 0. Постоянная распространения

Волновое сопротивление

Фазовая скорость

Длина волны

4. Для линии без потерь рассчитаем распределение вдоль линии действующих значений напряжения и тока.

Так как =0, то аргументом гиперболических функций является чисто мнимое число. Поскольку , то функции преобразуются к виду

Уравнение для напряжения и тока в любой точке линии запишутся в виде

Определим ток в конце линии , используя первое уравнение и полагая :

Напряжение в конце линии

Напряжение и ток в любой точке

Действующие значения напряжения и тока

Волновая длина линии

Возьмем ряд точек по длине линии (отсчитывая от ее конца) и результат сведем в таблицу 2.9.1.

Таблица 2.9.1

y,рад	0	/4	/2	3/4		5/4	3/2	7/4	2	2,45
y,км	0	2,14	4,28	6,42	8,56	10,7	12,8	15,0	17,1	21,0
cos y	1	0,71	0	-0,7	-1	-0,7	0	0,71	1	0,14
sin y	0	0,71	1	0,71	0	-0,7	-1	-0,7	0	0,99
U,В	64,5	194	213	110	64,5	194	213	110	64,5	220
I,A	0,23	0,12	0,07	0,21	0,23	0,12	0,07	0,21	0,23	0,04

Г рафики распределения действующих значений напряжения и тока имеют вид

Рис. 2.9-1

5. Определим действующие значения напряжения и тока в линии без потерь при согласованной нагрузке.

Основные уравнения имеют вид

Из приведенных формул следует, что модули комплексов в левой и правой частях одинаковы. Следовательно, действующие значения напряжения и тока неизменны по длине линии:

График распределения имеет вид

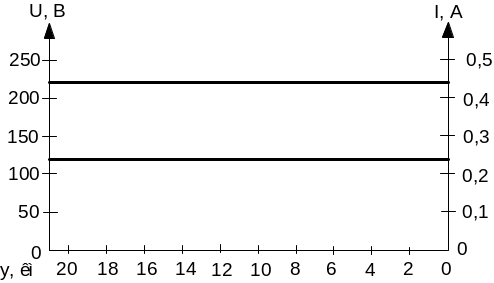
Рис. 2.9-2

Пример 10. Электростатическое поле точечных зарядов и заряженных осей (основные теоретические сведения приведены в п.1.9)

Дано:

Точечный заряд q и бесконечная ось с линейной плотностью заряда  расположены в вакууме над проводящей поверхностью (ось параллельна поверхности);

q=-510^-9 Кл; =2010^-8 Кл/м; h=2 см; a=3 см ;b=5 см.

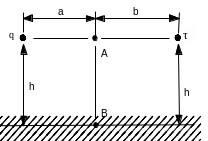
Рис. 2.10-1

Определить:

1. Напряженность электрического поля в точках А и В.

2. Разность потенциалов _А- _В.

3. Силу, действующую на точечный заряд , расположенный в точке А.

Решение:

1. Выражения для напряженности электрического поля могут быть получены из закона Гаусса:

Для точечного заряда поверхностью интегрирования является сфера S_c=4R², где R - радиус сферы; для оси - это боковая поверхность цилиндра S_ц=2Rl, где R, l – соответственно радиус и длина цилиндра. Для обоих случаев

Вектор одинаков по величине для всех точек выбранной поверхности и нормален к ней. Получаем для точечного заряда:

для заряженной оси:

Н аличие проводящей поверхности учитывается введением фиктивных зарядов, являющихся зеркальными отражениями действительных относительно поверхности. При этом фиктивные заряды равны, но противоположны по знаку действительным. Напряженность электрического поля в любой точке равна геометрической сумме напряженностей, создаваемых всеми заряженными телами. Направления векторов зависят от знаков зарядов. Составляющие вектора напряженности, созданные разными зарядами, показаны на рис.2.10-2

Рис. 2.10-2

Для точки А: .

Напряженность, создаваемая зарядом q:

Напряженность, создаваемая осью:

Напряженность, создаваемая отражением заряда q:

Напряженность, создаваемая отражением оси:

Для удобства расчетов свяжем с точкой А систему координат X0Y. Тогда горизонтальная составляющая поля в точке А

Знак " - " указывает на то, что E_X направлена противоположно оси Х. Вертикальная составляющая:

Результирующий вектор напряженности поля в точке А

Так как точка В лежит на проводящей поверхности, то горизонтальная составляющая поля Е_Х=0. В силу симметрии Е₁=Е₃, Е₂=Е₄. Вертикальная составляющая поля от заряда q

Вертикальная составляющая от заряженной оси

Величина результирующего вектора в точке В

Знак "-" указывает на то, что вектор поля в точке В направлен противоположно оси Y.

2. Разность потенциалов между точками А и В определяется выражением

Так как поле создается несколькими источниками, то сначала рассчитывается разность потенциалов от каждого источника в отдельности, а затем находится алгебраическая сумма этих составляющих. Путь интегрирования от А до В можно выбрать таким образом, что

.

Для точечного заряда

для заряженной оси

где R_A,R_B - расстояние от заряда или от оси до точек А и В. Разность потенциалов, создаваемая полем заряда q:

Разность потенциалов, создаваемая полем оси:

Разность потенциалов, создаваемая полем отражения заряда:

Разность потенциалов, создаваемая полем отражения оси:

Результирующая разность потенциалов

4. Сила, действующая на заряд в точке А:

Пример 11. Электростатическое поле в диэлектрике. Работа сил поля (основные теоретические сведения приведены в п.1.9)

Д ано:

По шаровому слою диэлектрика равномерно распределен заряд с объемной плотностью . Относительная диэлектрическая проницаемость диэлектрика и окружающей среды .

=210^-6 Кл/м³, =1; R₁=1 см; R₂=2 см; а=1 см.

Рис. 2.11-1

Определить:

1. Функции E= f(x),  = f(x), x [0,A] и построить их графики.

2. Работу, которую необходимо совершить при перемещении заряда из точки А в точку В.

Решение:

1. Выделим две области: 1 - область внутри диэлектрика R₁  x  R₂; 2 - область вне диэлектрика x > R₂. Для любой точки Х из области 1 по теореме Гаусса можно записать

Объем диэлектрика внутри поверхности интегрирования

Площадь сферической поверхности, через которую рассчитывается поток вектора :

Напряженность поля в первой области:

Для второй области уравнение Гаусса имеет вид

Здесь полный заряд диэлектрика равен

а выражение для напряженности поля имеет вид

Потенциал в первой области

Потенциал вне заряженного диэлектрика

где С₁ и С₂ - постоянные интегрирования.

Считаем, что в точках, бесконечно удаленных от области, потенциал равен нулю ₂()=0, тогда С₂=0. С₁ найдем из условия непрерывности потенциала на границе областей 1 и 2:

откуда

Окончательно выражения для потенциалов для областей внутри и вне диэлектрика имеют вид

Графики распределения напряженности и потенциала построим по данным таблицы 2.11-1.

Т аблица 2.11-1

	Область 1
Х, см	1	1,2	1,4	1,6	1,8	2
Е, В/м	0	348	646	892	1108	1310
, В	33,9	33,5	32,4	30,8	28,8	26,3
	Область 2
Х, см	2,2	2,4	2,6	2,8	3	3,2
Е, В/м	1095	921	785	675	590	519
, В	24	22	20	19	18	17

Рис. 2.11-2

2. Работа по перемещению заряда из точки А в точку В равна произведению величины этого заряда на разность потенциалов в точках А и В

Знак "-" указывает на то, что работа совершается против сил поля, т.е. потенциальная энергия заряда увеличивается.

Пример 12. Электрическое поле в несовершенном диэлектрике (основные теоретические сведения приведены в п.1.9)

Дано:

Пространство между обкладками сферического конденсатора заполнено несовершенным диэлектриком с удельной проводимостью =210^-7 См/м и диэлектрической проницаемостью =4. Радиусы обкладок R₁=1 см; R₂= 1,2 см. Заряд конденсатора Q=510^-9 Кл.

Определить:

1. Емкость и энергию конденсатора.

2. Полный ток утечки и мощность тепловых потерь.

Решение:

1. Выберем сферическую поверхность с радиусом

R₁  x  R₂ и запишем для нее уравнение по теореме Гаусса:

Разность потенциалов между обкладками конденсатора

Емкость конденсатора

Энергия электрического поля конденсатора

2. Так как диэлектрик является несовершенным (т.е. фактически проводником), то при наличии на обкладках разности потенциалов через конденсатор будет протекать ток утечки, плотность которого определяется законом Ома в дифференциальной форме:

С другой стороны, плотность тока определяется полным током утечки и площадью сферической поверхности, проходящей через данную точку:

Отсюда полный ток утечки

Мощность тепловых потерь

Для любой точки Х диэлектрика объем соответствующей шаровой поверхности определяется

Так как Е зависит только от х, то интеграл у по объему сводится к интегралу по координате х

П ример 13. Магнитное поле системы проводников с током (основные теоретические сведения приведены в п.1.10)

Рис. 2.13-1

Дано:

Проводники с токами I₁=1 А, I₂=3 А, I₃=2,5 А, I₄=1,5 А расположены в вершинах прямоугольника со сторонами а=5 м и b=7 м .Точки А и В расположены в середине соответствующих сторон.

Определить:

1. Напряженность магнитного поля в точках А и В.

2. Разность скалярных магнитных потенциалов между ними.

Решение:

1. Направления токов, проходящих перпендикулярно плоскости листа, указаны на рисунке. Напряженность магнитного поля, создаваемого проводником с током, определяется из закона полного тока:

Контуром интегрирования удобно выбрать окружность с радиусом r, в центре которой расположен проводник с током, плоскость окружности перпендикулярна проводнику. Тогда напряженность поля одинакова в любой точке контура, а векторы совпадают по направлению. Таким образом, напряженность поля, создаваемого одиночным проводником с током, в точке, удаленной на расстояние r от проводника, определяется как

Если поле создается системой токов, то определяется векторная сумма напряженностей от отдельных проводников. В частности, для точки А получаем

Направление вектора поля связано с направлением тока правилом правого винта: если связать направление тока с направлением движения острия винта, то направление поля будет совпадать с направлением вращения его головки.

Для удобства расчетов свяжем с точкой А систему координат Y0X. Составляющая поля по оси Х

Составляющая по оси Y

Косинусы и синусы углов  и :

Результирующее поле в точке А

Аналогично определяется вектор напряженности магнитного поля в точке В:

Разность магнитных потенциалов между точками А и В, создаваемая током I₁, определяется выражением

Путь интегрирования состоит из двух участков: отрезка радиальной прямой и участка дуги окружности. При движении по радиусу _m=0, так как векторы перпендикулярны. При движении по дуге

где ₁ - угол, на который опирается рассматриваемый участок дуги.

.

Аналогично определяются значения _m, образованные полями других токов:

Результирующая разность магнитных потенциалов равна алгебраической сумме этих составляющих. При этом если для данной составляющей направление движения по дуге от точки А к точке В совпадает с направлением вектора , то она учитывается со знаком "плюс", в противном случае - со знаком "минус".

Пример 14. Магнитное поле проводника с током с учетом границы раздела сред (основные теоретические сведения приведены в п.1.10)

Дано:

Линейный проводник с током I = 2 А бесконечной длины проходит параллельно плоскости раздела двух сред с относительными магнитными проницаемостями ₁=800 Гн/м и ₂ =1000 Гн/м,

а =1 м и h =0,5 м.

Определить напряженность магнитного поля в точках А и В

.

Решение:

Магнитное поле тока в неоднородной среде рассматривается как совокупность нескольких магнитных полей, каждое из которых может быть рассчитано по закону полного тока. В данном

случае расчет распадается на два этапа.

1. Расчет поля в верхнем полупространстве (точка А) осуществляется в соответствии с рис.2.14-2. При этом оба полупространства заполняет среда с магнитной проницаемостью ₁. Поле определяется заданным током I и фиктивным током I₁, который является зеркальным отражением I, а величина фиктивного тока определяется выражением

Напряженность поля, создаваемого током I:

Напряженность поля, создаваемого током I₁:

Результирующая напряженность поля в точке А

2. Расчет поля в нижнем полупространстве (точка В) осуществляется при условии, что обе среды имеют магнитную проницаемость ₂, а в месте заданного тока расположен фиктивный ток I₂, величина которого определяется выражением

Тогда напряженность поля в точке

Рис. 2. 14-3

Направление вектора показано на рис.2.14-3. Следует отметить, что направления фиктивных токов I₁ и I₂ принимаются такими же, как и направление заданного тока I. Из приведенных формул следует, что ток I₂ всегда положителен, т.е. совпадает по направлению с током I, а ток I₁ может быть как положительным, так и отрицательным, что определяется соотношением ₁ и ₂.

Пример 15. Магнитное поле катушки с сердечником (основные теоретические сведения приведены в п.1.10)

Дано:

Кольцевой сердечник катушки имеет магнитную проницаемость , площадь поперечного сечения S, средний радиус R, воздушный зазор . Ток катушки I, число витков w.

=1000; S=1 см²; R=10 см;

=1 см; I=1 A; w=500.

Рис. 2.15-1

Определить:

1. Индуктивность катушки.

2. Силу, стремящуюся уменьшить зазор.

Решение:

1. Считаем, что напряженность магнитного поля одинакова во всех точках сердечника и равна Н₁. Напряженность поля в воздушном зазоре Н₂. По закону полного тока

где l₁ - длина средней магнитной линии в сердечнике, .

Из условия непрерывности магнитного потока следует, что магнитная индукция постоянна во всех точках поля (и в сердечнике, и в зазоре). Магнитная индукция и напряженность поля связаны соотношением

где - магнитная постоянная.

Выразим напряженности поля через В. Для зазора =1, поэтому

Уравнение полного тока имеет вид

Решим его относительно магнитной индукции:

Напряженности поля определяются:

Энергия магнитного поля в сердечнике

Энергия магнитного поля в воздушном зазоре

Полная энергия катушки

Индуктивность катушки

Индуктивность катушки можно определить и другим путем. После определения индукции рассчитаем полный магнитный поток катушки:

После чего индуктивность определяется

Заметим, что полученным выражением можно воспользоваться и для расчета индуктивности соленоида. Если бесконечно увеличивать радиус катушки, то участки кольца конечной длины l будут практически прямолинейными. Тогда если на участок длиной l приходится W витков с током I, то напряженность и магнитная индукция в соленоиде:

Отсюда

2. Если в сердечнике имеется воздушный зазор, то возникает сила, которая стремится его уменьшить. Предположим, что под действием этой силы зазор уменьшился на величину dx. При этом совершена работа dA = Fdx. Энергия магнитного поля в зазоре изменится на величину

где - изменение объема зазора.

Так как dA = dW, то сила определяется:

Пример 16. Индуктивность проводника кольцевого сечения (основные теоретические сведения приведены в п.1.10)

Дано:

Прямолинейный проводник с током кольцевого сечения имеет магнитную проницаемость =1000 Гн/м, длина проводника l=10 м.

R₁=1 см, R₂=1,5 см, I= 3 А.

Определить внутреннюю индуктивность проводника.

Рис. 2.16-1

Решение:

Для любой точки, лежащей на расстоянии Х от центра проводника по закону полного тока можно записать

где I_х - ток, протекающий по части проводника, ограниченной радиусами R₁ и X:

Отсюда напряженность магнитного поля

Энергия магнитного поля

где V - объем рассматриваемой части проводника

Подставим его в выражение для напряженности и получим

Индуктивность проводника

При R₁0 получим формулы для сплошного цилиндрического проводника:

Пример 17. Электромагнитная индукция. Работа сил в магнитном поле (основные теоретические сведения приведены в п.1.11)

Дано:

В однородном магнитном поле с индукцией В=0,01 Тл, вращается прямоугольная рамка с проводником, размеры рамки а=10 см, b=30 см, сопротивление проводников R=0,1 Ом, угловая скорость вращения =250 с^-1.

Рис. 2.17-1

Определить:

1. Мгновенные и действующие значения наводимой ЭДС и

тока в рамке.

2. Совершаемую работу для поворота рамки на четверть периода.

Решение:

1. Ось вращения перпендикулярна направлению силовых линий магнитного поля. Будем считать, что вращение начинается из положения, когда нормаль к плоскости рамки совпадает с вектором . Для любого момента времени проекция на нормаль определяется:

.

Магнитный поток, пронизывающий рамку:

Мгновенное и действующее значения наводимой ЭДС

Мгновенное и действующее значения тока в рамке

2. Работа сторонних сил за четверть периода

Энергия, выделяемая в проводнике за тот же отрезок времени