
619_Sidel'nikov_G._M._Statisticheskaja_teorija_radiotekhnicheskikh_
.pdf
p(y1/x1) |
y1 |
x1 |
|
p(y2/x1) |
p(y1/x2) |
|
x2 
 y2 p(y2/x2)
y2 p(y2/x2)
Рис. 3.9. Граф однородного двоичного канала
На этом рисунке x1 и x2 – сигналы на входе канала связи, y1 иy2 – сигналы на выходе. Вероятности переходов указаны на Рис. 3.9. Если канал симметричный, то вероятности переходов попарно равны.
Обозначим:
p(y2/x1)=p(y1/x2)= pош – вероятность ошибки, p(y1/x1)=p(y2/x2)=1 pош – вероятность правильного приёма. В соответствии с формулами (3.4) и (3.5)
|
C max |
1 |
H y H y / x . |
|
|
||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||
Если сигналы x1 и x2 имеют одинаковую длительность э, то |
э . Тогда |
||||||||||||
пропускная способность канала будет равна |
|
|
|
|
|||||||||
|
C max |
1 |
|
|
H y |
H y / x |
|
|
|||||
|
|
|
|
|
|||||||||
|
э |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
В этой формуле maxH(y)=logk. Для двоичного канала (k=2) maxH(y)=1 и |
|||||||||||||
формула (3.8) примет вид |
|
|
|
|
|
|
|
|
|||||
|
C max |
1 |
1 H y / x |
|
|
||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
э |
|
|
|
|
||
Остаётся определить условную энтропию H(y/x): |
|
|
|||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
2 |
2 |
|
|
H y / x p xi y j log p y j |
/ xi p xi p y j / xi log p y j / xi |
||||||||||||
i 1 j 1 |
|
|
|
|
i 1 j 1 |
|
|
||||||
p x1 p y1 |
/ x1 log p y1 / x1 p x1 p y2 |
/ x1 log p y2 |
/ x1 |
||||||||||
p x2 p y1 / x2 log p y1 / x2 p x2 p y2 / x2 log p y2 |
/ x2 |
||||||||||||
p x1 1 pош log 1 pош p x1 pош log pош |
|
|
|||||||||||
p x2 pош log pош p x2 1 pош log 1 pош
pош log pош 1 pош log 1 pош .
Подставив это значение условной энтропии в выражение для пропускной способности канала, то получим:
41
C |
1 |
1 p |
log p |
1 p |
log 1 p |
|
(3.35) |
||
|
|||||||||
|
|
|
|
ош |
ош |
ош |
ош |
|
|
|
э |
|
|
|
|
|
|
||
C, бит/с
1/ э
pош
0 |
0,5 |
1 |
|
|
|
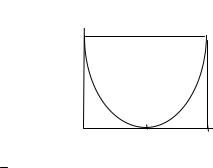
3.10. Зависимость пропускной способности от вероятности ошибки в канале
На рис. 3.10. построен график зависимости пропускной способности двоичного симметричного канала от вероятности ошибки.
Для канала с k>2 пропускная способность определяется почти аналогичной формулой:
C |
1 |
log k p |
log |
pош |
|
1 p |
log 1 p |
|
(3.36) |
||
|
|
||||||||||
|
|
|
|
ош |
|
k 1 |
ош |
ош |
|
|
|
|
э |
|
|
|
|
|
|
||||
В заключении рассмотрим один пример. Пусть имеется двоичный источ-
ник с производительностью H x |
1 |
1000 бит/c. |
|
||
|
э |
|
Если вероятность искажения pош =0,01, то из этого следует, что из 1000
элементов сигнала, переданных за одну секунду, в среднем 990 элементов будут приняты без искажений и только 10 элементов будут искажены. Казалось бы, пропускная способность в этом случае будет составлять 990 бит в секунду. Однако вычисление по формуле (3.10) даёт нам величину, значительно меньшую (C=919 бит/с). В чём здесь дело? А дело в том, что мы получили бы C=990 бит/с, если бы точно знали, какие именно элементы сообщения искажены. Незнание этого факта (а это практически знать невозможно) приводит к тому, что 10 искажённых элементов настолько сильно снижают ценность принимаемого сообщения, что пропускная способность резко уменьшается.
Другой пример. Если pош =0,5, то из 1000 переданных элементов 500 не
будут искажены. Однако теперь уже пропускная способность будет составлять не 500 бит/с, как можно бы предполагать, а формула (3.10) даст нам величину C=0. Действительно при pош =0,5 сигнал по каналу фактически уже не проходит
и канал просто эквивалентен генератору шума.
При pош 1 пропускная способность приближается к максимальной вели-
чине. Однако в этом случае сигналы на выходе системы необходимо инвертировать.
42

3.11. . Пропускная способность непрерывного канала
Если x(t) – сигнал на входе канала, а y(t)=x(t)+n(t) – сигнал на его выходе (n(t)– аддитивная помеха), то скорость передачи информации по непрерывному каналу будет определяться выражением (3.31), в котором величину 1/ надо заменить на 2Fmax ( или 2Fk , предполагая, что источник сигнала согласован с каналом и его полоса пропускания Fk= Fmax)
R x, y 2F h y h y / x |
(3.37) |
|
k |
|
|
где, как и ранее, h(y) – это энтропия выходного сообщения, h(y/x) – энтропия шума (почему она так называется, будет видно из дальнейшего изложения).
Дифференциальные энтропии в этом случае определяются по соответствующим формулам (3.19) и (3.20).
Пропускная способность равна максимально возможной скорости передачи по каналу, когда источник сигнала полностью согласован с характеристиками канала
C 2F |
max h y h y / x |
(3.38) |
||
k |
|
|
|
|
Максимум h(y) достигается в случае гауссовского закона распределения |
||||
случайной величины y. При этом |
|
|
|
|
max h y log |
|
|
|
|
2 e y2 |
(3.39) |
|||
При учёте влияния помехи необходимо рассматривать наихудший случай, когда помеха распределена также по гауссовскому закону.
Условная вероятность w(y/x), используемая при определении h(y/x), – это попросту ФПВ случайной величины y при якобы известном заранее значении x, хотя величина x является случайной. Но, так как y(t)=x(t)+n(t), можно записать
|
|
1 |
|
x n 2 |
|
|
|
|
|||
w y / x |
|
|
|
|
|
|
|
|
|||
|
e 2 y2/ x , |
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
2 y/ x |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
где 2y/x – дисперсия величины y при известном значении x, то есть дис- |
|||||||||||
персия помехи 2 . |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
Определим условную дифференциальную энтропию h(y/x): |
|
||||||||||
|
|
|
|
|
1 |
|
|
x n 2 |
|
||
|
|
|
|
|
|
|
|
|
|||
h y / x m log w y / x m log |
|
|
|
|
2 |
. |
|||||
|
|
|
e |
|
2 n |
||||||
|
|
|
|
||||||||
|
2 n |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
В этом выражении предполагается, что x известно заранее. Таким образом, величина x в приведенном выражении является попросту математическим ожиданием величины y. Однако известно, что энтропия непрерывного случайного процесса от математического ожидания не зависит.
43
Тогда получаем, что
|
|
1 |
||
|
|
|
||
h y / x m log |
|
|
|
|
|
|
|
||
|
|
2 n |
||
|
|
|
|
|
n2
e 2 2 m log w n h n .
n
Отсюда видно, почему в данном случае условная энтропия h(y/x)=h(n) и называется дифференциальной энтропией шума.
Для гауссовского закона распределения помехи максимальное значение энтропии шума, в соответствии с (3.14), будет равно
max h y / x h |
n log |
|
|
|
|
|
|
|
|||||
|
2 e 2 |
(3.40) |
|||||||||||
|
max |
|
|
|
|
|
|
|
n |
|
|
||
Подставляя (3.14) и (3.15) в (3.13), получаем |
|
|
|
|
|||||||||
C 2F log |
|
|
|
|
|
|
|
y |
. |
||||
2 e 2 |
log |
2 e 2 |
2F log |
||||||||||
|
|||||||||||||
k |
y |
|
|
|
|
|
n |
|
k |
n |
|||
Введя число 2 под знак логарифма, получим |
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|||||
|
C F log |
|
y |
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
k |
|
2 |
|
|
|
|
|||||
|
|
|
|
|
n |
|
|
|
|
||||
В этом выражении 2n=Pп – мощность помехи, а 2y= 2x+ 2n=Pк+Pп, где Pк – мощность сигнала на выходе канала. С учётом этого получаем окончательно формулу для вычисления пропускной способности непрерывного канала связи
(формулу Шеннона): |
|
|
|
|
|
|
|
|
|
|
|
Pk |
|
|
log 1 h2 |
|
|
C Fk |
log 1 |
|
|
Fk |
(3.41) |
|||
|
||||||||
|
|
|
Pп |
|
|
|
||
h2 – отношение мощности сигнала к мощности помехи (отношение сигнал/шум в канале).
В заключение можно отметить следующее. Для достижения скорости передачи информации по непрерывному каналу, близкой к пропускной способности канала, сигнал x(t) по статистической структуре должен быть близок к флюктуационной помехе (белому шуму) с гауссовским законом распределения.
ГЛАВА 4. ОСНОВЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
4.1.Классификация решающих устройств
Решающим устройством (РУ) называется устройство, реализующее прави-
ло выбора решенияФ x t |
, которое является статистическим, так как |
|
|
|
|
сигналыx(t) и шумыn(t) на его входе являются, как правило, случайными величинами или процессами (рис. 4.1.).
44
x(t) xT |
|
Г |
|
РУ |
|||
|
|
||
|
|
|
Ф[x(t)]
Рис. 4.1. Решающее устройство
Втеории статистических решений ставится и решается задача синтеза оптимальных решающих устройств. В СТРТС эти задачи решаются в приложении
ктеории и практике приема сигналов в условиях шума.
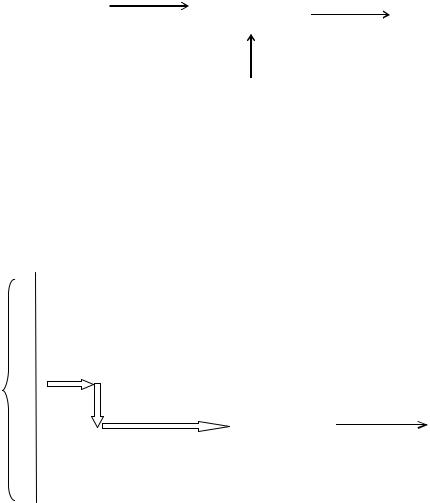
Вприёмном устройстве РУ может располагаться как до, так о после демодулятора (детектора). При этом одноканальное РУ имеет один вход, многоканальное – к входов(рис. 4.2.).
k
Векторное поле: |
|
x t,k , |
0 t T ; |
k V -координаты пространства.
V
РУ |
γ |
|
|
0
Рис. 4.2. Многоканальное РУ
Сигнал во всех каналах содержит одну и ту же информацию. Общий процесс, из которого выделяется нужная информация, является векторным случайным процессом
x |
t |
|
|
1 |
|
|
|
x2 |
t |
x t, k ,0 t T. |
(4.1) |
|
|
||
... |
|
|
|
|
|
|
|
xк |
t |
|
|
Многоканальное РУ позволяет организовывать систему пространственновременного наблюдения.
Если РУ имеет один выход, то это однофункциональное РУ; многофункциональное РУ имеет несколько выходов. Например, решающее устройство решает задачу обнаружения сигнала в шумах и измерение значения какого-либо
45

из его параметров (амплитуды, фазы и пр.).
По априорным сведениям о сигнале на входе РУ разделяются:
полная априорная информация о входном процессе x(t), 0 t T (синтез при полностью известном сигнале): в этом случае вероятностная модель x(t) задана полностью в виде конечномерных функций плотности распределения
wn x,t , n 1,2,..., .
параметрическая априорная неопределенность о процессе x(t)(синтез при не полностью известном сигнале): вероятностная модель x(t) задана не полностью, с точностью до конечного числа параметров ,
wn x,t, ,n 1,2,...;
(может быть известна область возможных значений параметра ); параметр θ может быть векторным с m-компонентами
|
1 |
|
|
|
|
2 |
(4.2) |
|
|
||
m
непараметрическая априорная неопределенность о процессе x(t) (синтез при непараметрической неопределенности): вероятностная модель x(t) задана с точностью до бесконечного числа параметров, фактически не известна функция плотности распределения для данного момента времени t(может быть известно, что одномерная функция w1 x,t P0 (принадлежит классу Р0), например, клас-
су функций симметричных относительно 0).
Наиболее типичные задачи, решаемые в процессе синтеза РУ в зависимости от назначения РТС:
–обнаружение сигнала на фоне помех;
–различение сигналов на фоне помех;
–оценка параметров сигнала на фоне помех;
–различие двух сигналов и оценка их параметров;
–восстановление формы (фильтрация) сигнала.
Таким образом, любой приемник обязательно содержит хотя бы одно решающее устройство, которое в соответствии с некоторым правилом решения Ф(х), определяет значение информационного параметра (принимает решение о значении выходного сигнала γ, используя входной сигнал x(t)).
Рассмотрим постановку задачи синтеза РУ в зависимости от назначения РТС на следующих примерах.
Пример 4.1 Обнаружение сигнала.
При обнаружении сигнала на фоне помех в результате анализа сигнала x(t) на интервале 0 t T формулируется две гипотезы:
гипотеза Н0: x(t) – только помеха, то есть x(t)=n(t), 0 t T ;
46
гипотеза Н1: x(t) – смесь сигнала и помехи, |
|
x(t) S(t) n(t),0 t T |
(4.3) |
Врезультате должно быть найдено правило решения Ф x t , которое
позволит принять одну из указанных гипотез. При этом γ принимает два значения из множества Г→( γ0 ,γ1):
γ0 – справедлива гипотеза Н0, γ1 – справедлива гипотеза Н1.
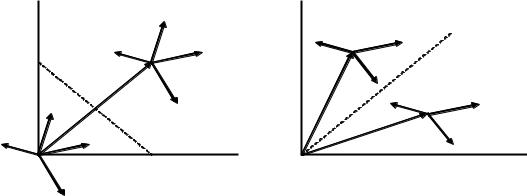
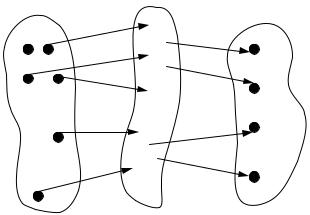
На рисунке 4.3а в некотором пространстве (система координат 1, 2) изображен вектор сигнала S, на который накладываются векторы помех с различными фазами и амплитудами (в любой момент времени к вектору сигнала добавляется один из векторов помех, причём на рисунке изображено несколько векторов помех, чтобы показать, что вектор помехи может иметь любую фазу и величину). Если сигнал S на входе приемника отсутствует, векторы помех исходят из начала координат (точка 0).
Для принятия решения о наличии или отсутствии сигнала на входе приемника, все пространство разбивается на два подпространства: подпространство сигнала (гипотеза Н1) и подпространство помех (гипотеза Н0). В зависимости от того, в какое подпространство попадает конец результирующего вектора, принимается решение о наличии или отсутствии сигнала на его входе. Граница
подпространств зависит от правила решения Ф x t и на рисунке показана
пунктиром. Если под действием помехи конец суммарного вектора (сигнал + помеха) попадает в подпространство Н0, имеет место пропуск сигнала; если, наоборот, конец вектора помехи без сигнала попадает в подпространство Н1,
имеет место ложная тревога.
1 |
|
|
1 |
|
|
n |
|
|
|
S |
|
0 |
n |
2 |
0 |
|
|
а) |
|
|
n |
S1 |
S2 |
|
n |
|
2 |
|
б) |
Рис. 4.1. Пространство сигналов и помех
При этом правило решения |
Ф x t |
является детерминированным, если |
|
|
|
|
|
при повторном появлении одной и той же реализации сигнала x(t)на входе всегда принимается одно и то же решение (т.е. внутри себя правило решения не содержит вероятностного алгоритма). Это означает, что детерминированное
47
правило решения устанавливает функциональное соответствие между множеством реализаций сигнала x(t)и множеством Г. В дальнейшем будут расматриваться только детерминированные правила решения.
Правило решения |
Ф x t |
является рандомизированным Ô |
x t |
, ес- |
||
|
|
|
|
ðàí ä |
|
|
ли оно устанавливает статистическую связь между входом и выходом (между множеством реализаций сигнала xi(t)и множеством Г ), Рис. 4.4.
Ф |
x t |
|
|
ранд |
|
Г |
|
XT |
|
|
|
|
k |
xi (t) |
Pk i |
|
Рис. 4.4. Рандомизированное правило решения
На рисунке 4.4 реализации сигнала xi t и решения k связаны вероятностью Pki ,где Pki i 0,1,...,m - совместная вероятность i-й реализации сигна-
ла на входе и k-го решения на выходе.
Следует отметить, что рандомизированное правило решения в среднем никогда не лучше детерминированного решения.
Пример 4.2 Различение двух разных сигналов (или m сигналов).
При различении двух сигналов на фоне помех в результате анализа сигнала x(t) на интервале 0 t T формулируется две гипотезы:
гипотеза Н0: x(t) – смесь сигнала S0(t).и помехи, то есть
x(t)=S0(t)+n(t), 0 t T ;
гипотеза Н1: x(t) – смесь сигнала S1(t).и помехи, то есть
x(t) S1(t) n(t),0 t T. |
(4.4) |
Врезультате должно быть найдено правило решения Ф x t , которое
позволит принять одну из указанных гипотез. При этом γ принимает два значения из множества Г→( γ0 ,γ1):
γ0 – справедлива гипотеза Н0, γ1 – справедлива гипотеза Н1.
Приемник решает, какой из сигналов (S1или S2 ) имеется на его входе ; на рисунке 4.3б показаны два вектора сигналов вместе с помехами. Все пространство сигналов и помех разбивается на подпространства по числу сигналов: в
48
данном случае подпространство сигнала S0(t) (гипотеза Н0) и подпространство сигнала S1(t) (гипотеза Н1). Приемник принимает решение в пользу той гипотезы, в подпространстве которой находится конец вектора суммы сигнала и помехи. Если под действием помехи конец суммарного вектора попадет в чужое подпространство, произойдет ошибка в принятии решения.
Следует иметь в виду, что, когда приемник предназначен для приема дискретных сигналов (обнаружение сигналов, различение сигналов), то, как правило, форма выходных сигналов не совпадает с формой сигналов на его входе. Например, если приемник осуществляет различение сигналов S1(t) = A cos 1t и S2(t) = A cos 2t, 0 t T (дискретная частотная модуляция), то при приеме сигнала S1(t) на выходе приемника будет импульс напряжения положительной полярности, а при приеме сигнала S2(t) - импульс отрицательной полярности (или 0, в зависимости от конкретной реализации схемы приемника).
В общем случае модель сигнала может быть представлена во временном пространстве в виде:
x t Sv t n t ,0 t T , (4.5) v {0,1...},
и в вероятностном пространстве в виде k-мерной функции плотности распределения: wn x,v , причем при изменении v может изменяться и вид функции. Параметр v обычно называется параметром состояния входного сигнала.
Пример 4.3 Оценка параметров сигнала.
Например, в РУ определяется амплитуда сигнала или величина его запаздывания. Такая задача решается в телеметрических системах, в радиолокации; при этом скорость изменения измеряемого параметра сигнала значительно меньше скорости измерения (то есть значение параметра не изменяется в процессе измерения).
В рассматриваемом примере на входе РУ всегда присутствует сигнал вместе с помехой
x t S t n t , 0 t T |
|
|
|
|
(4.6) |
где – параметр (амплитуда) с неизвестным значением из бесконечного |
|||||
множества возможных значений Θ. |
|
|
|
|
|
Необходимо определить значение амплитуды . |
|
|
|
|
|
ˆ |
x |
t |
, значение |
||
На выходе РУ по одной реализации получается оценка |
|
||||
|
i |
i |
|
|
|
которой зависит от конкретного вида реализации сигнала на входе, то есть оценка ˆ является случайной величиной.
49
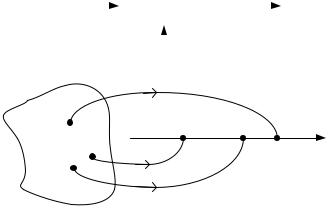
x(t, ) |
|
|
|
|
||
РУ |
|
|||||
|
|
|
||||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Ф[x(t)] |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||
ˆ |
ˆ |
|
3 |
1 |
|
xi (t, ) |
|
|
|
ˆ |
|
|
|
2 |
Рис. 4.5. Оценка параметра сигнала
Разные реализации дают разные точки около истинного значения параметра .
Таким образом, в решении задачи ставится соответствие множеству реализаций сигнала xi (t) xT через правило решения Ф x множество оценок ампли-
туды сигнала ˆi .
Пример 4.4 Различие двух сигналов с неизвестными параметрами.
При различении двух сигналов с неизвестными параметрами на фоне помех в результате анализа сигнала x(t) на интервале 0 t T формулируется две гипотезы:
гипотеза Н0: x(t) – смесь сигнала S0(t).и помехи, то есть |
|
|
x t S0 t, 0 |
n t , 0 t T ; |
|
гипотеза Н1: |
x(t) – смесь сигнала S1(t) и помехи, то есть |
|
x t S1 t, 1 n t , 0 t T |
|
|
|
или , x(t) Sv (t, ) n(t) |
(4.7) |
где , - векторный параметр с двумя компонентами:λ – непрерывная компонента, v– дискретная компонента.
Истинное значение параметра λ неизвестно. При этом, если v =0, то 0 ; если v =1, то 1 , то есть при изменении параметра состояния v может изменяться и пространство решений (рис 4.6).
(v 0) 0 (v 1) 1
50
