619_Sidel'nikov_G._M._Statisticheskaja_teorija_radiotekhnicheskikh_

Дальнейшее повышение информационной, спектральной и энергетической эффективности связано с увеличением кратности (позиционности) модуляции.

Для линейных процессов модуляции, к которым относится амплитудная и фазовая модуляция справедлив принцип суперпозиции, то есть, возможно изменение параллельно двух параметров несущего колебания. В этой связи используется обычно варианты амплитудно-фазовой модуляции. Для повышения спектральной эффективности методов модуляции необходимо повышение позиционности модуляции. При этом важным становится выбор варианта созвездия сигнальных точек, обеспечивающих наибольшую спектральную и энергетическую эффективность.

Если рассматривать увеличение позиционности фазовой модуляции, то увеличение количества сигнальных точек приводит к уменьшению помехоустойчивости. Мерой, определяющей помехоустойчивость, является эквивалентная энергия ансамбля сигналов численно равная минимальному расстоянию между сигнальными точками. С повышением позиционности фазовой модуляции минимальное расстояние уменьшается, поэтому на практике не используются сигналы с фазовой модуляции с числом позиций больше 8. Другими словами, при фазовой модуляции сигнальное созвездие используется неэффективно. Более благоприятным является сигналы с квадратурной амплитудной модуляцией (QAM).

Алгоритм формирования сигналов с квадратурной амплитудной модуляцией представляет собой разновидность многопозиционной амплитуднофазовой модуляции.

При использовании данного алгоритма передаваемый сигнал кодируется одновременными изменениями амплитуды синфазной (I) и квадратурной (Q) компонент несущегогармонического колебания, которые сдвинуты по фазе друг относительно на π/2. Результирующий сигнал S(t) формируется при суммировании этих колебаний. Таким образом, QAM модулированный сигнал может быть представлен :

Где d – энергетическая база сигнала, Ac(α) и As(β) косинусные и синусные квадратурные компоненты амплитуд сигнала, зависящие от векторов дискрет-

ных параметров α = [α1, α2,, α3, …. Αn] , β = [β1, β2,, β3, …. βn], fc – номинальное значение несущей частоты, α и β принимают значение [+1,-1].

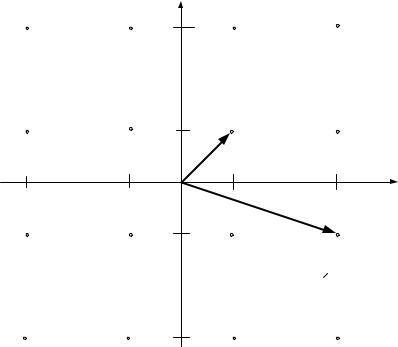
Для 4QAM выражение (2.12) приобретает вид:

S(t) = d{αcos(2πfct) + βsin(2πfct)}

где α = ±1, β = ±1 в зависимости от значений информационных символов

21

Для 16QAM:

где α1 = ±1, α2 = ±1, α3 = ±1, β1 = ±1, β2 = ±1, β3 = ±1.

Q

3

На рис. 2.4 представлено сигнальное созвездие QAM-16, где отмечены кодовые слова в соответствии с алгоритмом манипуляционного кода Грея. Применение кода Грея позволяет сделать расстояния между сигналами эквидистантными, то есть, чем больше кодовое расстояние между кодовыми словами, тем больше удалены друг от друга сигнальные точки.

Выражения (2.13) и (2.14) с использованием кода Грея будут представлены

как:

22

Решетчатое расположение сигнальных точек получило наибольшее распространение на практике, так как позволяет увеличить минимальное расстояние для QAM -16 между сигналами в 1,6 раза по сравнению PSK – 16.

3.ТЕОРИЯ ИНФОРМАЦИИ

3.1.Энтропия и производительность дискретных источников

3.1.1.Мера количества информации

Информацияэто совокупность сведений о некотором объекте или явлении, которые увеличивают знания потребителя об этом объекте или явлении.

Не всякое сообщение содержит информацию. В теории информации при передаче сообщений исходят из того, что в некотором сообщении xiколичество информации (xi)зависит не от её конкретного содержания, степени важности и т.д., а от того, каким образом данное сообщение выбирается из общей совокупности возможных сообщений. В реальных условиях выбор конкретного сообщения производится с некоторой априорной вероятностью p(xi). Чем меньше эта вероятность, тем больше информации содержится в данном сообщении [6].

При определении количества информации в сообщении предполагается,

что:

количественная мера информации должна обладать свойством аддитивности: количество информации в нескольких независимых сообщениях равняется сумме количества информации в каждом сообщении;

количество информации о достоверном событии, когда p(xi)=1, должно равняться нулю, так как такое сообщение не увеличивает наших знаний о данном объекте или явлении;

Указанным условиям удовлетворяет логарифмическая мера, определяемая формулой

Чаще всего логарифм берется с основанием 2, реже с основанием e: I xi log2 p xi двоичных единиц информации (бит),

I xi ln p xi натуральных единиц информации (нит).

Одну двоичную единицу информации содержит сообщение, вероятность выбора которого равняется 1/2. В этом случае

I xi log2 12 log2 2 1дв. ед. инф. (бит).

Учитывая, что в практике передачи и преобразования информации широко применяются двоичные символы, двоичная логика, двоичные источники сообщений и двоичные каналы передачи, наиболее часто используется двоичная единица информации (бит).

23

В теории информации чаще всего необходимо знать не количество инфорцииI(xi), содержащееся в отдельном сообщении, а среднее количество информации в одном сообщении, создаваемом источником.

Если имеется ансамбль (полная группа) из k сообщений x1, x2...xi,xkс вероятностями p(xi) ... p(xk), то среднее количество информации, приходящееся на одно сообщение и называемое энтропией источника сообщений H(x), определяется формулой

Энтропия характеризует источник сообщений с точки зрения неопределённости выбора того или другого сообщения.

Рассмотрим свойства энтропии.

Чем больше неопределённость выбора сообщений, тем больше энтропия. Неопределённость максимальна при равенстве вероятностей выбора каждого

сообщения: p(x1)=p(x2)= . . .=p(xi)=1/k.

В этом случае

(т.е. максимальная энтропия равна логарифму от объёма алфавита). Например, при k=2 (двоичный источник) Hmax x log2 2 1 бит.

2. Неопределённость минимальна, если одна из вероятностей равна единице, а остальные нулю (выбирается всегда только одно заранее известное со-

общение, например, одна буква): p(x1)=1; p(x2)= p(x3)= ... = p(xk)= 0. В этом случае H(x)=Hmin(x)=0.

Эти свойства энтропии иллюстрируются следующим образом.

Пусть имеется двоичный источник сообщений, т.е. осуществляется выбор всего двух букв (k=2): x1 и x2 , p(x1)+ p(x2)= 1.

Тогда

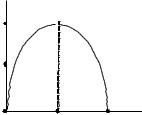
Зависимость H(x) от вероятностей выбора для двоичного источника приведена на Рис. 3.1.

24

Рис. 3.1. Энтропия двоичного источника

Укрупним алфавит. Пусть на выходе двоичного источника имеется устройство, которое группирует буквы в слова из n букв. Тогда k = 2n слов (объём алфавита). В этом случае

Таким образом, укрупнение алфавита привело к увеличению энтропии в n раз, так как теперь уже слово включает в себя информацию n букв двоичного источника. Тем самым доказывается свойство аддитивности энтропии.

Энтропия дискретного источника не может быть отрицательной.

Термин “энтропия” заимствован из термодинамики и применительно к технике передачи информации предложен американским учёным К. Шенноном, в трудах которого были заложены основы теории информации (математической теории связи).

Ранее при определении энтропии предполагалось, что каждое сообщение (буква или слово) выбирается независимым образом. Рассмотрим более сложный случай, когда в источнике сообщений имеются корреляционные связи. В так называемом эргодическом источнике выбор очередной буквы сообщения зависит от конечного числа предшествующих букв n. Математической моделью такого источника является марковская цепь n-го порядка, у которой вероятность выбора очередной буквы зависит от n предшествующих букв и не зависит от более ранних, что можно записать в виде следующего равенства:

где с - произвольное положительное число.

Если объем алфавита источника равен k, а число связанных букв, которые необходимо учитывать при определении вероятности очередной буквы, равно порядку источника n, то каждой букве может предшествовать M=kn различных сочетаний букв (состояний источника), влияющих на вероятность появления очередной буквы xi на выходе источника. А вероятность появления в сообщении любой из k возможных букв определяется условной вероятностью (3.6) с учётом предшествующих букв, т.е. с учётом M возможных состояний. Эти состояния обозначим как q1,q2...qM.

Сказанное поясним двумя простыми примерами.

25

Пример 1. Пусть имеется двоичный источник (объём алфавита k=2) например, источник, выдающий только буквы аи б; порядок источника n=1. Тогда число состояний источника M=kn=21=2(назовём их состояния q1 иq2). В этом случае вероятности появления букв аи б будут определяться следующими условными вероятностями:

p(à/q1=а), p(а/q2=б), p(б/q1=а), p(б/q2=б),

где q1=а - 1-е состояние q1,

q2=б - 2-е состояние q2.

Вероятности состояний источника p(q1)=p(a), p(q2)=p(б).

Пример 2. Пусть по-прежнему k=2 (буквы а и б), однако число связанных букв n=2. Тогда M=22=4 (4 возможных состояния: (а, а)=q1, (а, б)=q2, (б,а)=q3,

(б, б)=q4 .

В этом случае имеем дело со следующими условными вероятностями: p(а/а,а); p(а/а,б);p(а/б,а); p(а/б,б); p(б/а,а) . . . и т.д.

Вероятности состояний определяются равенствами p(q1)=p(a,a), p(q2)=p(a,б), p(q3)=p(б,a), p(q4)=p(б,б).

Энтропия эргодического дискретного источника определяется в два этапа.

Вычисляется энтропия источника в каждом из M состояний, считая эти состояния известными:

k

для состояния q1 H x / q1 p xi / q1 log p xi / q1 ;

i 1

k

для состояния q2 H x / q2 p xi / q2 log p xi / q2 ;

i 1

k

для состояния qM H x / qM p xi / qM log p xi / qM .

i 1

2. Далее находим H(x) путём усреднения по всем состояниям q:

M

H x p q j H x / q j .

j 1

Окончательно получаем

При наличии корреляционных связей между буквами в эргодическом источнике энтропия уменьшается, так как при этом уменьшается неопределённость выбора букв и в ряде случаев часть букв можно угадать по предыдущим или ближайшим буквам.

3.1.2. Совместная и взаимная энтропия двух источников

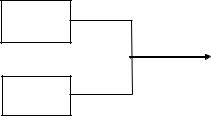
Пусть имеется два дискретныхисточника с энтропиями H(x) и H(y) и объёмами алфавитов k и l (рис. 3.2).

26

H(x)

H(x, y)

H(y)

Рис. 3.2. Объединение двух источников

Объединим оба эти источника в один сложный источник и определим совместную энтропию. Элементарное сообщение на выходе системы содержит элементарное сообщение xiи сообщение yj. Алфавит сложной системы будет иметь объём k l, а энтропия будет равна

ij

условная энтропия источника y относительно источникаx. Она показывает, какую энтропию имеют сообщения y, когда уже известно сообщение x.

Если источники независимы, то p(y/x)=p(y) и H(y/x)=H(y). В этом случае

H(x, y)=H(x)+H(y).

Если источники частично зависимы, то H(x, y)<H(x)+H(y).

Если источники полностью зависимы (x и y cодержат одну и ту же ин-

формацию), то H(y/x)=0 и H(x, y)=H(x)=H(y).

На рис. 3.3 показана (условно) собственная энтропия H(x) и H(y), условные энтропии H(x/y) и H(y/x) и совместная энтропия H(x, y). Из этого рисунка, в частности, следуют соотношения (3.9) и (3.10).

27

Рис. 3.3. Разновидности информации

Часть рисунка, отмеченная двойной штриховкой, называется взаимной информацией H x y . Она показывает, какое (в среднем) количество информа-

ции содержит сообщение x о сообщении y (или наоборот, сообщение y о сообщении x). Как следует из рисунка 3.3,

Если сообщение x иy полностью независимы, то взаимная информация отсутствует и H x y = 0. Если x иy полностью зависимы ( x и y содержат

одну и ту же информацию), то H x y H x H y .

Понятие взаимной информации очень широко используется в теории передачи информации. Требования к взаимной информации различны в зависимости от того, с какой информацией мы имеем дело. Например, если x иy это сообщения, публикуемые различными газетами, то для получения возможно большей суммарной (совместной) информации взаимная (т.е. одинаковая в данном случае) информация должна быть минимальной. Если же x иy это сообщения на входе и на выходе канала связи с помехами, то для получения возможно большей информации её получателем необходимо, чтобы взаимная информация была наибольшей. Тогда условная энтропия H(x/y) – это потери информации в канале (ненадежность канала), H(y/x) – это дополнительная ин-

формация (энтропия помех в канале – H(n)).

3.1.3. Избыточность и производительность источника

Как было показано ранее, энтропия максимальна при равновероятном выборе элементов сообщений и отсутствии корреляционных связей. При неравномерном распределении вероятностей и при наличии корреляционных связей между буквами энтропия уменьшается.

Чем ближе энтропия источника к максимальной, тем рациональнее работает источник. Чтобы судить о том, насколько хорошо использует источник свой алфавит, вводят понятие избыточности источника сообщений

28

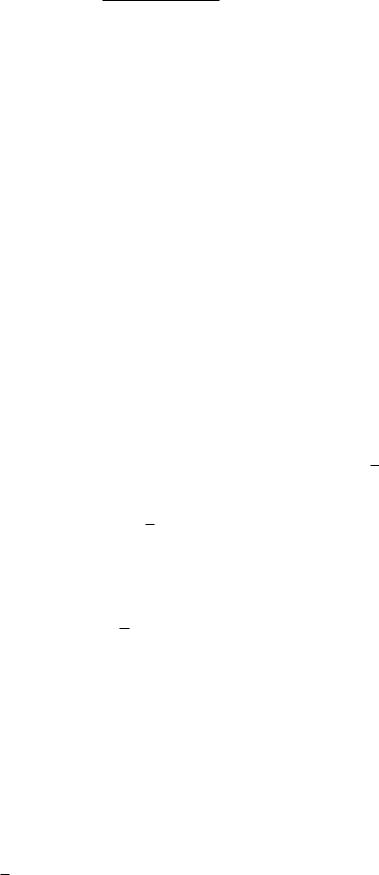
Hmax (x) H (x) 100%

Hmax (x)

Наличие избыточности приводит к загрузке канала передачи информации передачей лишних букв сообщений, которые не несут информации.

Однако, преднамеренная избыточность в сообщениях иногда используется для повышения достоверности передачи информации — например, при помехоустойчивом кодировании в системах передачи информации с исправлением ошибок. Большую избыточность имеет любой разговорный язык. Например, избыточность русского языка (как и других) около 50%. Благодаря избыточности облегчается понимание речи при наличии дефектов в произношении или при искажениях речевых сигналов в каналах связи.

Производительность источника определяется количеством информации, передаваемой в единицу времени. Измеряется производительность количеством двоичных единиц информации (бит) в секунду. Если все элементы сообщения имеют одинаковую длительность , то производительность

Если же различные элементы сообщения имеют разную длительность, то в приведённой формуле надо учитывать среднюю длительность , равную математическому ожиданию величины i:

i p i .

i 1K

Однако в последней формуле p( i)можно заменить на p(xi) (вероятность i- го сообщения), так как эти вероятности равны. В результате получаем

i 1

апроизводительность источника будет равна

Mаксимально возможная производительность дискретного источника

Для двоичного источника, имеющего одинаковую длительность элементов сообщения (k=2, ) имеем

29

При укрупнении алфавита в слова по n букв, когда k=2n, n , имеем

Таким образом, если производительность источника максимальна, то путём укрепления алфавита увеличить производительность источника нельзя, так как в этом случае и энтропия, и длительность сообщения одновременно возрастают в одинаковое число раз.

В то же время известна теорема К.Шеннона, которая утверждает следую-

щее: Если источник сообщений имеет производительность H (x)<H max(x), то можно закодировать сообщения таким образом, чтобы увеличить производительность источника до величины сколь угодно близкой к величине H max(x), но не превзойти её.

3.2.Статистическое кодирование дискретных сообщений

Используя теорему К. Шеннона, сформулированную в предыдущем разделе, можно увеличить производительность источника дискретных сообщений, если априорные вероятности различных элементов сообщения неодинаковы. К.Шеннон предложил и метод такого кодирования, который получил название статистического или оптимального кодирования. В дальнейшем идея такого кодирования была развита в работах Фано и Хаффмена и в настоящее время широко используется на практике для “cжатия сообщений”.

Основой статистического (оптимального) кодирования сообщений является теорема К. Шеннона для каналов связи без помех [1,6].

Кодирование по методу Шеннона-Фано-Хаффмена называется оптимальным, так как при этом повышается производительность дискретного источника, и статистическим, так как для реализации оптимального кодирования необходимо учитывать вероятности появления на выходе источника каждого элемента сообщения ( учитывать статистику сообщений) .

Используя определения производительности и избыточности дискретного источника, приведённые в (3.13) и (3.16), можно получить

H x 1 Hmax x 1 .

Из этой формулы видно, что для увеличения производительности нужно уменьшать избыточность или среднюю длительность сообщений .

Идея статистического кодирования заключается в том, что, применяя неравномерный неприводимый код, наиболее часто встречающиеся сообщения (буквы или слова) кодируются короткими кодовыми словами этого кода, а редко встречающиеся сообщения кодируются более длительными кодовыми словами.

30