619_Sidel'nikov_G._M._Statisticheskaja_teorija_radiotekhnicheskikh_

Когда время задержки лучей соизмеримо с длительностью посылки сигнала, необходимо учитывать какие символы передавались до и после основного символа.

С учетом (4.14) и (4.15) выражения (4.16) и (4.17) примут вид

a,с = 0,1.

Для определения вероятности ошибочного приема необходимо анализировать последовательность на трех тактовых интервалах

Итак, рассмотрим двоичные ДЧМ сигналы

Выражение (20) и (21) записаны в общем виде для ДЧМ. Если n = 1, то мы имеем сигналы с минимальным частотным сдвигом с непрерывной фазой разнесенных на 1/Т, Т – длительность посылки (прямоугольная огибающая сигнала). Если n = ∞, то сигналы 0 и 1 занимаю значительную полосу.

Так как используем некогерентный прием, то важна величина: 0 1 . Если Ψ = 0, то сигналы (4.20) и (4.21) с непрерывной фазой, если Ψ = π, то

сразрывами фазы (использование двух генераторов).

Всоответствии с (11):

a,b,c, r 0,1

Подставляя в (22) значение S0(t) и S1(t) получаем

162

165

раний переход от непрерывной фазы к разрыву фазы значительно уменьшается. При увеличении порядка разнесения М это отличие нивелируется.

Анализ помехоустойчивости системы с МСИ был проведен для частотной корреляционной функции, имеющей нормальное распределение. Для условий приема сигналов с подвижными объектами в условиях города такая зависимость характерна для полного затенения прямого луча или многокаскадного переприема сигналов с одного подвижного объекта на другой. При небольшом удалении или когда высота антенн выше уровня крыш, распределение задержек можно представить в виде экспоненциального распределения [3]:

где τ > 0, К – среднеквадратическое отклонение времени задержек, 2 – мощность рассеянного сигнала.

В соответствии с приведенной выше методикой получим эквивалентное отношение сигнал-шум для модели канала (26). Для этого в выражение (23) для определения моментов необходимо подставить (26) и определить функции автокорреляции (22) для односторонней МСИ.

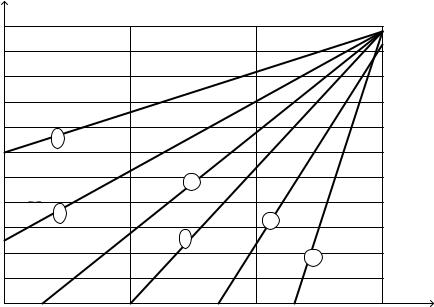
Рис. 7.10. Зависимости вероятности неустранимой ошибки для сигналов ДЧМ при n = ∞ для модели ( 3) и (26) от d и М:

экспоненциальная модель ─ − ─ = 1, −− М = 2, − − − М = 4, нормальная модель ── М = 1, −∙∙ −∙∙− М = 2, — — — М = 4.

166

Для экспоненциальной модели расширения задержек получены следующие выражения:

Выражение (27) получено для n = ∞.

Зависимости, показанные на рисунке 4 позволяют сделать вывод, что одностороннее распределение МСИ при равных условиях значительно хуже двустороннего и при увеличении порядка разнесения расхождение не уменьшается, как это происходит при n = ∞ , Ψ = 0 и Ψ = π. При увеличении порядка разнесения (М >4 ) разница между системой с непрерывной фазой, с разрывом фазы и n = ∞ практически отсутствует.

Рис. 7.11. Зависимость вероятности неустранимой ошибки для сигналов ДОФМ —— , и для сигналов ДЧМ с непрерывной фазой — — от d

при различном порядке разнесения М (1 и 3 М = 1), (2 и 5 М = 2), (4 и 6 М = 4).

Как показано на рис.7.11 помехоустойчивость некогерентного приема сигналов ДЧМ с непрерывной фазой значительно выше чем помехоустойчивость когерентного приема ДОФМ [4]. Известно, что в канале с Гауссовским аддитивным шумом ситуация полностью противоположная. В канале с частотноселективными замираниями определяющим является структура формирования межсимвольной интерференции (МСИ). Величина МСИ определяется в первую очередь автокорреляционными свойствами сигналов , формой огибающей, длительностью посылки, полосой когерентности и в последнюю очередь методом приема и моделью канала. В соответствии с методикой рассмотренной выше, проигрыш сигналов ДОФМ связан с тем, что информация вкладывается

167

не в абсолютное значение параметра сигнала, а в разность их (порядок модуляции), тем самым формируя МСИ на большем количестве посылок. Увеличение порядка модуляции приводит к увеличению МСИ на величину порядка [20].

Таким образом можно сделать следующие выводы.

Вданной работе показано, что для канала с непрерывной многолучевостью исследование помехоустойчивости в условиях частотно-селективных замираний возможно с применением формул (5) – (8) , которые накладывают ограничения , а именно, сложение некоррелированных сигналов с равными весами, прием сигналов на согласованный фильтр с последующим получением квадратичной формы, последетекторное сложение сигналов.

Дан сравнительный анализ помехоустойчивости сигналов с разной структурой и показано, что основным фактором снижения помехоустойчивости является соотношение между длительностью посылки сигнала и полосой когерентности (или среднеквадратическое отклонение задержанных лучей); выбор модели канала существенного значения не имеет.

Вусловиях города, где полоса когерентности лежит в диапазоне от 0,1 МГц до 1 МГц уменьшение длительности посылки возможно только при использовании разнесенного приема, при этом минимальное ее значение равно 4 мкс ( в 50% случаев).

8.ПОМЕХОУСТОЙЧИВОСТЬ СИГНАЛОВ С В КАНАЛАХ

СДИСКРЕТНОЙ МНОГОЛУЧЕВОСТЬЮ

8.1.Сравнительный анализ межсимвольной интерференции

сигналов с ФРМ и ФМ

Анализ помехоустойчивости дискретных систем связи в каналах с частот- но-селективными замираниями, как правило, основан на применении аппарата системных функций [16]. Такой анализ не отображает всего многообразия многолучевого поля и не применим для сигналов с кратностью модуляции более двух. Кроме того многолучевое поле носит дискретный характер, так как используются высоко поднятые антенны [14].

Целью данной главы является рассмотрение аналитических выражений для расчета параметров межсимвольной интерференции фазоразностной и фазовой модуляции различной кратности. В основу положена двухлучевая модель канала, где вторым лучом может являться как сигнал другой станции, так и совокупность отраженных лучей [20-22].

Информационным параметром сигнала при фазоразностной модуляции яв-

ψ = φ n – φ n-1

Для составления математических алгоритмов работы приемника удобно представить посылки сигнала Sn -1(t) и Sn (t) в виде векторов Sn -1 и Sn функционального пространства сигналов. Аппарат векторной алгебры целесообразно использовать в связи с тем, что понятие разности фаз двух посылок сигнала и угла между соответствующими векторами функционального протранства тождественны.

В отсутствии помех в векторной алгебре угол ψ между векторами Sn -1 и Sn заданными на интервале T , определяется из следующего общего соотношения

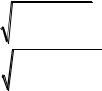
где Sn-1·Sn - скалярное произведение векторов, Sn 1 , Sn - нормы векторов Sn (t) и Sn-1 (t), равные

Однако при наличии помех и межсимвольной интерференции (МСИ)

cos ψ ≠ cos ( φn - φ n-1 )

Ниже рассмотрим случай образования МСИ в двухлучевом канале с постоянными параметрами.

Суммарный сигнал на интервале (n -1)T ≤ t ≤ nT при задержке τз < T

где A0 A0 – амплитуда основного луча, AЗ – амплитуда задержанного луча, τЗ – величина задержки второго луча относительно первого основного луча.

Суммарные вектора сигналов на двух посылках можно представить как: