619_Sidel'nikov_G._M._Statisticheskaja_teorija_radiotekhnicheskikh_
.pdf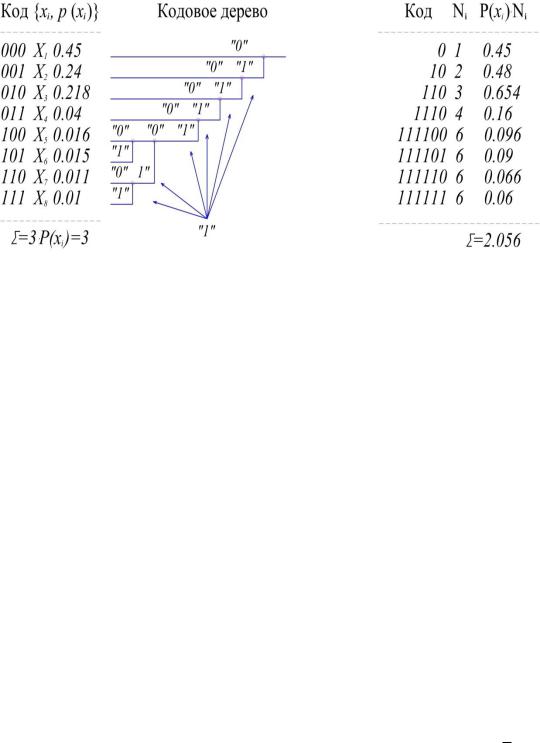
Рассмотрим принципы оптимального кодирования на приводимом ниже примере. Пусть источник сообщений выдаёт 8 различных сообщений x1 ... x8с
вероятностями 0,495; 0,4; 0,026; 0,02; 0,018; 0,016; 0,015; 0,01 (сумма вероятно-
стей равна 1).
Располагаем эти сообщения столбцом в порядке убывания вероятностей
(Рис. 3.4).
Рис. 3.4. Статистическое кодирование
Объединяем два сообщения с самыми минимальными вероятностями двумя прямыми и в месте их соединения записываем суммарную вероятность: p(x7)+p(x8)=0,011+0,01=0,021. В дальнейшем полученное число 0,021 учитываем в последующих расчётах наравне с другими оставшимися числами, кроме чисел 0,011 и 0,01. Эти уже использованные числа из дальнейшего расчёта исключаются. Далее таким же образом объединяются числа 0,015 и 0,016, получается число 0,031, затем вновь объединяются последующие числа и т.д.
Построенное таким образом кодовое дерево используется для определения кодовых слов нового кода. Напомним, что для нахождения любого кодового слова надо исходить их корня дерева (точка с вероятностью 1) и двигаться по ветвям дерева к соответствующим сообщениям x1...x8. При движении по верхней ветви элемент двоичного кода равен нулю, а при движении по нижней – равен единице. Например, сообщению x5 будет соответствовать комбинация 111100. Справа от кодового дерева записаны кодовые слова полученного неравномерного кода. В соответствии с поставленной задачей, наиболее часто встречающееся сообщение x1 (вероятность 0,45) имеет длительность в 1 элемент, а наиболее редко встречающиеся имеют длительность в 6 элементов. В двух последних столбцах рисунка приведено число элементов Ni в кодовом сло-
8 |
|
|
|
|
|
|
|
p |
x |
N |
i |
2,056 |
представляет собой |
ве и величина произведения p(xi) Ni. |
|
i |
|
|
i 1
число элементов, приходящееся на одно слово, т.е. в данном случае 2,056 э
31
Если бы для кодирования был применён равномерный двоичный код, который чаще всего применяется на практике, число элементов в каждом кодовом слове для кодирования восьми различных сообщений равнялось бы трём (23=8), т.е. 3 э . В рассматриваемом примере средняя длительность кодового слова
благодаря применённому статистическому кодированию уменьшилась в 3/2,056=1,46 раза. Во столько же раз увеличилась и производительность источника.
Дальнейшим развитием оптимального статистического кодирования является кодирование кодовых слов. В этом методе применяется также оптимальное кодирование по методу Шеннона-Фано-Хаффмена, однако не к отдельным буквам, а к кодовым словам( сочетаниям n букв первичного сообщения). Статистическое кодирование слов позволяет ещё больше уменьшить среднюю длительность сообщений, так как алфавит источника быстро увеличивается с увеличением длины слова. Число возможных кодовых слов (алфавит источника после объединения букв) определяется выражением m=kn, где k - алфавит букв первичного сообщения.Пусть, например, у нас имеется двоичный источник с алфавитом а1 и а2 (например, “1” и “0”). При передаче этих букв по каналу связи используются сигналы длительностью э, а э .
Рассмотрим пример, когда p(а1)=0,8 и p(а2)=0,2 (если вероятности p(а1)и p(а2) равны между собой, никакое кодирование не может уменьшить среднюю длительность сообщения). Образуем из элементов а1 и а2 слова из двух букв(n=2), беря различные сочетания из этих букв. Если у нас источник с независимым выбором элементов сообщений, то
p(а1а1)=0,8 0,8=0,64; p(а1а2)=p(а2а1)=0,8 0,2=0,16; p(а2а2)=0,2 0,2=0,04.
Применяя к полученным словам кодирование по методу Шеннона–Фано, получаем кодовое дерево (Рис. 3.5.), из которого видно, что новые кодовые слова неравномерного кода имеют длительность э, 2 э и 3 э.
Средняя длина кодового слова
сл 0,64 э 0,16 2 э 0,16 3 э 0,04 3 э 1,56 э .
Но так как каждое слово содержит информацию о двух буквах первичного сообщения, то в расчёте на 1 букву получаем 0,78 э . Отсюда видно, что
средняя длина элемента сообщения сократилась по сравнению с первоначаль-
ной в 1/0,78=1,38 раза.
Рис. 3.5. Алфавит источника после объединения букв
32
Если усложнить кодирование и использовать n=3, то в этом случае получим 0,724 э . Это уже почти предел, дальше уменьшать уже нецелесооб-
разно. Чтобы убедиться в этом, рассчитаем производительность источника сообщений для всех трёх случаев.
Энтропия источника
Hx p(a1) log p(a1) p(a2 ) log p(a2 )
0,8log2 0,8 0, 2log2 0, 2 0,722бит.
При отсутствии статистического кодирования э ,
H x 0,722 бит/с.
э
При кодировании слов по две буквы : 0,78 э ,
|
|
0,722 |
|
|
|
|
0,926 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
x 0,78 э |
|
|
э |
бит/с. |
|||||||
|
|
|||||||||||
|
|
|
|
0,724 э |
||||||||
При кодировании по две буквы : |
|
|||||||||||
|
|
0,722 |
|
|
|
|
0,997 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0,724 э |
|
|
|
|
|
|
||||||
H |
|
|
э |
бит/с. |
||||||||
Последняя величина близка к предельно возможной величине 1/ э. Статистическое кодирование слов целесообразно применять также в слу-
чае использования эргодического дискретного источника (источника с корреляционными связями букв), так как объединение букв в слова приводит к разрушению корреляционных связей (величина n должна быть не менее порядка эргодического источника, а n э , соответственно, больше интервала корреляции букв первичного сообщения). Корреляционные связи между буквами трансформируются в различные вероятности появления возможных слов (n - буквенных сочетаний). При этом необходимо помнить, что вероятность n-буквенных сочетаний определяется не произведением вероятностей отдельных букв, а, в соответствии с теоремой умножения вероятностей надо учитывать также условные вероятности. Так, например, для источника с независимым выбором букв p(a1a1)=p(a1) p(a1), а для эргодического источника с корреляционными связями букв p(a1a1)=p(a1) p(a1/a1).
3.3.Энтропия и производительность непрерывных источников
Определение энтропии источников непрерывных сигналов (далее непрерывных источников) является более сложной задачей по сравнению с определением энтропии дискретных источников. Ограничим решение задачи практически важным случаем определения энтропии источников стационарных непрерывных сигналов с ограниченным спектром. Стационарный случайный сигнал с ограниченным спектром Fс является стационарным случайным процессом, который (в соответствии с теоремой Котельникова) полностью определяется своими отсчётами, взятыми через интервалы времени t 1 (2Fс ) . Значения
33
процесса в отсчётах являются непрерывными случайными величинами x с одинаковой плотностью распределения вероятностей w(x). Поэтому в этом случае задача определения энтропии непрерывного источника сводится к задаче определения энтропии непрерывных случайных величин.
Энтропия дискретного случайного сигнала определяется выражением (3.2). Для непрерывной случайной величины воспользуемся этим же выражением, заменив вероятность p(x)наw(x)dx.
В результате получим
H x
w x dx log w
x dx |
|
|
w x log w x log dx dx . |
|
|
|
|||
|
|
|
|
|
Но логарифм бесконечно малой величины (dx) равен минус бесконечности, в результате чего получаем
Hx w x log w x dx .
Таким образом, энтропия непрерывной случайной величины бесконечно велика. Но так как в последнем выражении первое слагаемое ( ) от величины x или от w(x) не зависит, то при определении энтропии непрерывной величины учитывается только второе слагаемое (“добавка” к бесконечности). Эта добавочная энтропия (в отличие от энтропии дискретноых случайных величин) по-
лучила название дифференциальная энтропия случайной величины и определя-
ется формулой
h x m log w x |
|
|
|
|
|
|
|||
|
w x log w x dx |
(3.19) |
||
В дальнейшем слово “дифференциальная” в определении энтропии будем иногда опускать.
Как и для дискретных сообщений, существуют следующие разновидности дифференциальной энтропии непрерывной величины.
1. Условная энтропия случайной величины y относительно случайной величины x.
|
|
|
|
h y / x m log w y / x |
w2 |
x, y log w y / x dxdy |
(3.20) |
2.Совместная энтропия двух непрерывных случайных величин равна
x, y m log w y, x w2 x, y log w2 x, y dxdy (3.21)
Для независимых xи yh(x,y)=h(x)+h(y).
Для совместной дифференциальной энтропии непрерывной случайной величины справедливы соотношения (3.8) и (3.9).
3. Взаимная энтропия h(x y), содержащаяся в двух непрерывных величи-
34
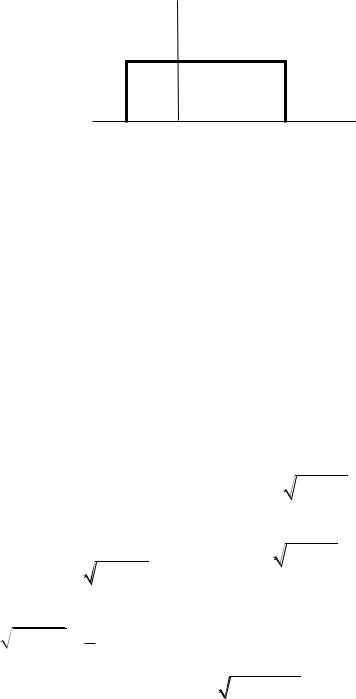
нах x и y, определяется формулой (3.13).
Для независимыхxи y взаимная энтропия h(x y)=0.
4. Если случайная величина ограничена в объёме V=b-a, то её дифференциальная энтропия максимальна при равномерном законе плотности распределения этой величины (рис.3.6).
w(x)
|
|
a |
|
|
|
b |
x |
|
|
Рис. 3.6. Равномерная функция плотности вероятностей |
|
||||||||
hmax x |
b |
1 |
|
1 |
dx log b a logV |
|
|||
|
|
log |
(3.22) |
||||||
|
|
|
|
||||||
b |
a |
b a |
|||||||
|
|
|
|
|
|||||
|
a |
|
|
|
|
|
|
||
Энтропия hmax(x) не зависит от математического ожидания случайной величины x , так как эта величина зависит только от разности (b-a), а не от абсолютных величин b иa.
5. Если случайная величина не ограничена в объёме (т.е. может изменяться в пределах от - до + ), а ограничена только по мощности, то дифференциальная энтропия максимальна в случае гауссовского закона распределения этой величины. Определим этот максимум.
В соответствии с (3.19)
h x m log w x , где w x |
|
1 |
|
e |
x a 2 |
|
|
|
2 2 . |
||||
|
|
|
||||
2 2 |
||||||
|
|
|
|
|
Отсюда
|
|
|
|
|
|
x a |
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x a |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|||||||
h |
x m log |
|
|
|
e |
2 |
|
|
|
|
log |
2 |
|
m |
2 2 |
|
log e . |
|
|
|
|
|
|
|
|
||||||||||||
2 2 |
|
|
|
|
|
|||||||||||||
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Но математическое ожиданиеm (x-a2) = 2, отсюда получаем hmax x log 
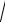2 2 12 log e , или окончательно
|
x log |
|
|
h |
2 2 e |
(3.23) |
|
max |
|
|
|
Cледовательно, энтропия зависит только от мощности 2.
Эта очень важная формула будет использоваться позднее для определения пропускной способности непрерывного канала передачи информации.
35
Заметим, что, как и ранее, hmax(x) не зависит от математического ожидания a случайной величины x. Это важное свойство энтропии. Оно объясняется тем, что математическое ожидание является неслучайной величиной.
Случайный сигнал x(t) длительностью Tс, отображающий непрерывное сообщение с ограниченным спектром Fс , в соответствии с теоремой Котельнико-
ва полностью определяется k T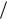
t отсчётными значениями. Знание значений
сигнала между отсчётами не увеличивают сведений о сигнале. Следовательно, при определении энтропии непрерывного сигнала достаточно учитывать только его отсчётные значения.
Известно, что энтропия обладает свойством аддитивности. Так, если у ка- кого-то дискретного сигнала энтропия равна H(x), то энтропия сигнала, составленного из nэлементов, будет равна n H(x). Аналогичным образом можно вычислить энтропию непрерывного сигнала длительностью T, которая будет равна
k h1 x 2Fс Tс h1 x ,
где h1(x) – дифференциальная энтропия одного сечения случайного сигнала, определяемая по формуле (2.29) через одномерную плотность вероятности. Размерность энтропии h1(x) – бит на один отсчёт случайного сигнала (одно сечение из k сечений случайного процесса).
Соответственно производительность непрерывного источника будет равна
|
|
x |
h x |
|
|
2Fс Tс h1 x |
|
|
h |
Tс |
|
Tс |
|
||||
или |
|
|
|
|
|
|
|
|
|
x 2Fс h1 |
x |
бит/с |
(3.24) |
||||
h |
||||||||
Таким образом, производительность источника непрерывного сигнала полностью определяется энтропией одного отсчета и удвоенной полосой частот этого сигнала.
3.4.Эпсилон-энтропия источника непрерывных сообщений
Сигнал на выходе источника (И) рис. 3.7. непрерывных сообщений (например, микрофона, телефона, датчика температуры и пр. ) представляет собой непрерывный случайный процесс, энтропия которого в любом из сечений в общем случае равна бесконечности . Такое количество информации не может быть передано по реальному каналу связи, пропускная способность которого всегда ограничена. Это и не нужно, так как скорость восприятия информации любым потребителем на выходе канала всегда ограничена его физическими возможностями. Поэтому непрерывный сигнал на выходе канала связи даже без помех отличается от сигнала на входе, так как содержит не всю информацию о нем (причем под каналом связи можно понимать любое преобразование одного ансамбля сигналов в другое: модуляцию, усиление, дискретизацию и пр.). Уже преобразование непрерывного сообщения в сигнал соответствующим
36
устройством( микрофоном или др. датчиком сигнала) связано с потерей части информации, а сигнал отображает сообщение лишь с некоторой точностью
(t) [x(t) xˆ(t)] ,
где x(t – сигнал на входе преобразователя; xˆ(t) – сигнал на выходе преоб-
разователя (Пр) или оценка входного сигнала преобразователем, который всегда представляет собой некоторое решающее устройство, работающее по определенному правилу и заданному критерию качества.
|
|
|
|
|
|
|
|
|
|
|
|
|
xˆ(t) |
|
|
|
|
|
x(t) |
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
Пр |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
h (t) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.3.7. - энтропия |
|
||||||||
Критерий качества, как известно, определяется потребителем информации, |
|||||||||||||
например, среднеквадратическое отклонение |
|
||||||||||||
|
|
|
ñð (t) m{[x(t) xˆ(t)]2} |
(3.25) |
|||||||||
или дисперсия ошибки |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
m 2 |
(t) . |
|
|||||
Эпсилон-энтропией H (x)( - энтропией) называется минимальное количество информации, которое должно содержаться в выходном сигнале xˆ(t) о
входном сигнале x(t), чтобы этот сигнал можно было восстановить с заданной точностью ср.
ˆ |
ˆ |
(3.26) |
he x minI (x, x) h x maxh(x / x), |
||
где: |
|
|
I(x, xˆ )-взаимная информация x и xˆ |
; |
|
h(x) и h(x/ xˆ )- соответственно, дифференциальная энтропия сигнала x(t) и условная энтропия x(t), когда xˆ(t) известно; min и max берутся по всевозмож-
ным условным ФПВ w(x/ xˆ ).
В общем случае, когда сигнал (или сообщение) x(t) является гауссовским с
дисперсией 2 |
, ошибка (t) также является гауссовской с дисперсией |
2 |
, а с |
x |
|
|
|
учетом аддитивного характера ошибки (t) условная энтропия h(x/ xˆ ) |
полно- |
||
стью определяется дифференциальной энтропией h( ). Соответственно, maxh(x/
|
|
|
|
|
|
|
|
|
|
xˆ )= maxh( )= log( |
2 e) . |
|
|
|
|
|
|
|
|
Тогда - энтропия одного сечения гауссовского источника ( - энтропия од- |
|||||||||
ного отсчета) |
|
|
|
|
|
|
|
|
|
h x log( |
|
|
|
|
|
|
|
|
|
x |
2 e) log( |
|
2 e) 0,5 log( 2 |
2 ). |
(3.27) |
||||
|
|
|
|
|
x |
|
|
||
37
Величина 2 |
2 |
показывает отношение мощности(дисперсии) сигналаx(t) |
x |
|
|
к мощности (дисперсии) ошибки, при котором среднеквадратическое отклонение сигналов x(t) и xˆ(t) не превышает .
Следовательно, производительность источника непрерывных сообщений можно определить как количество информации, которое необходимо передавать в единицу времени, чтобы восстановить сообщение с заданной точностью.
h’ |
x v h |
x , |
(3.28) |
|
|
|
|
где v=1/ t - скорость передачи отсчетов на выходе источника, t - интервал между отсчетами.
Для стационарного сигнала с ограниченным спектром t=1/(2Fmax), тогда
h’ (x)= 2Fmax h (x).
Если, кроме того, источник является гауссовским, то
’ |
2 |
2 |
|
(3.29) |
h x Fmax |
. log x |
|
Количество информации, выдаваемое гауссовским источником за время Tc, равно
’ |
Fmax |
2 |
2 |
|
(3.30) |
Tc h x Tc |
log x |
|
что совпадает с формулой для объёма сигнала, когда динамический диапазон сигнала
Dc= log x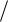2 
2 .
Это значит, что объем сигнала на выходе источника равен количеству информации, которое содержится в сигнале для его воспроизведения с заданной точностью.
Для канала с пропускной способностью С, на входе которого подключен источник с производительностью h’ (x), теорема К.Шеннона для канала с шумами принимает вид:
Если при заданном критерии точности источника (например, ) его эпсилон – производительность меньше пропускной способности канала h’ (x)< С, то существует способ кодирования (преобразования сигнала), при котором неточность воспроизведения сколь угодно близка к ; приh’ (x)> С такого способа не существует.
Теорема К.Шеннона определяет предельные возможности согласования источника непрерывных сообщений с каналом связи. Практически это достигается применением помехоустойчивых видов модуляции и кодирования.
3.5.Скорость передачи информации и пропускная способность канала
Всистеме передачи дискретных сигналов при отсутствии помех информация на выходе канала связи (канала ПИ) полностью совпадает с информацией на его входе, поэтому скорость передачи информации численно равна произво-
38
дительности источника сообщений: |
|
|
|
|
|
R x, y |
H x |
H x |
(3.31) |
||
|
|
|
|||
|
|
|
|
|
|
При наличии помех часть информации источника теряется и скорость передачи информации оказывается меньшей, чем производительность источника. Одновременно в сообщение на выходе канала добавляется информация о поме-
хах (Рис. 3.8.) [1,6].
Рис. 3.8. Структурная схема канала передачи информации по каналу с помехами
Поэтому при наличии помех необходимо учитывать на выходе канала не всю информацию, даваемую источником, а только взаимную информацию:
|
R x, y |
I x y |
бит/с. |
(3.32) |
||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На основании формулы (2.28) имеем |
|
|
|
|
|
|
||||||||
или |
R x, y |
1 |
H x H x / y |
|
1 |
H y H y / x , |
||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
где H (x) производительность источника;
H (x/y) ненадёжность “ канала(потери) в единицу времени; H (y) энтропия выходного сообщения в единицу времени; H (y/x)=H’(n) –энтропия помех ( шума) в единицу времени.
Пропускной способностью канала связи (канала передачи информации) C называется максимально возможная скорость передачи информации по каналу
C max R x, y |
(3.33) |
Для достижения максимума учитываются все возможные источники на входе и всевозможные способы кодирования.
Таким образом, пропускная способность канала равна максимальной производительности источника на входе канала, полностью согласованного с ха-
39
рактеристиками этого канала, за вычетом потерь информации в канале из-за помех.
В канале без помех C=maxH (x), так как H (x/y)=0. При использовании
равномерного кода с основанием k, состоящего из n элементов длительностьюэ, в канале без помех
|
|
H x |
|
log k n |
log k |
|
|||||
|
C max |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
n |
|
|
|
||||
|
|
|
|
|
э |
э |
|
||||
при k=2 |
C 1 э бит/c. |
|
|
|
|
|
|
|
|
|
|
Для эффективного использования пропускной способности канала необходимо его согласование с источником информации на входе. Такое согласование возможно как для каналов без помех, так и для каналов с помехами на основании двух теорем, доказанных К.Шенноном. Для согласования источника с каналом без помех используется статистическое (или эффективное) кодирование.
Для согласования источника с каналом в присутствии помех используется теорема К. Шеннона (для каналов с помехами):
Если пропускная способность канала равна C, а производительность источника H’(x)<C, то путём соответствующего кодирования можно передавать информацию по каналу со скоростью, сколь угодно близкой к C и с вероятностью ошибки, сколь угодно близкой к нулю. Если же H’(x)>C, то можно закодировать источник таким образом, что ненадёжность будет меньше, чем H’(x)-C+ , где – сколь угодно малая величина.
Не существует способа кодирования, обеспечивающего ненадёжность, меньшую, чем H'(x)-C.
К сожалению, теорема К.Шеннона для каналов с шумами(помехами) указывает только на возможность такого кодирования, но не указывает способа построения соответствующего кода. Однако известно, что при приближении к пределу, устанавливаемому теоремой Шеннона, резко возрастает время запаздывания сигнала в устройствах кодирования и декодирования из-за увеличения длины кодового слова n. При этом вероятность ошибки на выходе канала стремится к величине
n |
C |
|
H ( x) |
|
(3.34) |
p 2 э |
|
|
|
||
ош |
|
|
|
|
|
Очевидно, что pош 0, когда n э , и следовательно, имеет место “обмен” верности передачи на скорость и задержку передачи.
Внастоящее время известен довольно широкий класс помехоустойчивых кодов, обеспечивающих скорость и качество передачи, близкие к пределу, устанавливаемому теоремой Шеннона.
3.6.Пропускная способность двоичного симметричного канала
Воднородном канале связи без памяти условные (переходные) вероятно-
сти p(yj/xi) не зависят от времени и от того, какой символ передаётся. Граф состояний и переходов однородного двоичного канала приведен на Рис. 3.9.
40