Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

lection_part3

.pdf

Скачиваний:

Добавлен:

09.02.2015

Размер:

2.93 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2811 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

2)E =< E >=

=2 π 2n2 h2

a a2 2m

sin

πnx

(−

h2 d 2

(

sin

πnx

))dx =

∫

2m dx2

2 a

1−cos

2πnx

∫sin2 πnxdx =

∫

(

)dx =

a3m

π 2n2h2

(x −

2πnx

π 2n2h2

2a3m

sin

)

;

(3.43)

2πn

2a2m

πnx

sin

(−ih

(

sin

))dx

p =< p >= ∫

ihπn

2πnx

= −

πn ∫sin

πnx cosπnx dx = −

∫sin

dx =

a a 0 14a424a443

sin 2α

a = 0 .

ihπn

cos

2πnx

2πn

10.3.Потенциальный барьер. Туннельный эффект

Впредыдущем параграфе было рассмотрено движение частиц в ограниченной области пространства – финитное движение. Рассмотрим теперь случаи, в которых частица, находящаяся в силовых полях, способна уходить на бесконечность (инфинитное движение).

Если потенциальная энергия частицы в силовом поле имеет вид

0, x < 0,

U (x) =

U0 , x ≥ 0,

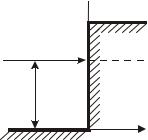
то такое поле называют потенциальным порогом (потенциальной стенкой) – поля с резкой границей. УШ (10.1) для областей 1 и 2 (рис. 10.5) соответственно примут вид:

d 2Ψ		2m
1	+		EΨ = 0,	(10.14)

dx2		h2	1

d 2Ψ		2m
2	+		(E −U	0	)Ψ = 0.	(10.15)

dx2		h2			2

Введём замену k = [2mE / h2 ]1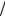2 , q = [2m(−E +U0 ) / h2 ]1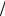2 (q – случай высокого потенциального порога).

101

1 U0 2

0 x

Рис. 10.5

Тогда уравнения (10.14), (10.15) можно записать в виде:


d 2Ψ1	+		2m			k 2Ψ = 0 ,	(10.16)

dx2				h2	1

d 2Ψ2		−		2m		q2Ψ = 0.	(10.17)

dx2				h2	2

Общее решение уравнения (10.16) в случае высокого ( E <U0 ) порога запишем в виде линейной комбинации линейно независимых функций –

суперпозиции плоских волн де Бройля без множителя e−iωt , так как рассматривается стационарная задача:

Ψ1(x) = A1eikx + B1e−ikx ,

где A1 – падающая на порог волна, B1 – отражённая от порога волна. Для

уравнения (10.17)

Ψ2 (x) = A2eqx + B1e−qx .

В силу конечности ВФ Ψ2 коэффициент A2 = 0. В силу того, что порог U0 имеет конечную высоту, ВФ Ψ на границе раздела областей 1 и 2

должна быть непрерывной и гладкой, т.е. иметь непрерывную производную.

Условия сшивки решений для областей 1 и 2:

Ψ1(0) = Ψ2 (0),

или

A1 + B1 = B2 ,

(10.18)

Ψ1′(0) = Ψ2′ (0),

ikA1 −ikB1 = −qB2.

Напомним, что коэффициенты

2 и

2 связаны с

плотностью

вероятности событий.

Например,

связан с вероятностью

отражения

частицы от порога,

2 – с вероятностью падения частицы на порог, а

– с вероятностью того, что частица может быть обнаружена в области 2 потенциального порога, являющейся с точки зрения КФ для неё запрещённой.

Плотность потока вероятности для частиц: 1) падающих на порог

102

пад

;

2) отражённых от порога

;

отр

3) прошедших в область порога 2:

jпрош = hmq В2 2 .

Тогда коэффициент отражения от порога (R от лат. reflection)

	jотр			В	2


R =		=	1			;
			1
	jпад			A	2


				1

прохождения через порог (прозрачность порога D или P )

	jпрош			В		2


D =		=	2				,
			2
	jпад			A	2


				1

причём по закону сохранения числа частиц:

R + D =1,

( jпад = jотр + jпрош ).

(10.19)

(10.20)

(10.21)

(10.22)

(10.23)

Для качественного анализа без потери общности решения положив A1 =1, из системы (10.18) получим:

B	=	k −iq	, B	2	=	2k	.	(10.24)

1		k +iq				k +iq

Система уравнений (10.18) имеет решение при любых значениях k и q ; это означает, что частица обладает непрерывным энергетическим

спектром. С учётом A1 =1 и (10.24) из (10.22) имеем:

R =	k −iq	2	→1.

	k +iq

С учётом A2 = 0 и равенств (10.24)

Ψ	(x) =	2k	e−qx .	(10.25)

2		k +iq

Из выражения (10.25) видно, что Ψ2 (x) отлична от нуля и уменьшается

с возрастанием x по экспоненциальному закону, а это означает, что существует отличная от нуля вероятность пребывания частицы под порогом

при E <U0 :

103

(x) =

Ψ(x)

2 exp(−2qx) =

k +iq

4k 2

exp(−

2m(U0 − E)x).

(10.26)

2 + q2

1h44424443

эВ=1,6 10-19 Дж,

Проводя расчёт согласно

(10.26)

для

U0–E=1

для двух

значений х=10-10 м и х=10-9 м, получим expα ≈ 0,29 и expα ≈ 4,58 10−8

соответственно. Это означает, что проникновение электрона в область высокого потенциального порога с заметной вероятностью возможно лишь на расстояния, сравнимые с размером атома.

Таким образом, хотя R →1(≈1), т.е. отражение является полным, оно

не обязательно произойдёт на самом пороге (на границе раздела). С некоторой вероятностью частица может проникнуть в область 2, а затем

выйти из неё.

( E >U0 ) потенциального

В случае низкого

порога аналогично

рассмотренному выше имеем:

2Ψ

+ k 2Ψ = 0 , k 2 =

для области 1

dx2

для области 2

d 2Ψ2

+ q2Ψ = 0, q2

(E −U

dx2

Решениями уравнений являются функции:

Ψ1(x) = A1eikx + B1e−ikx ,

Ψ2 (x) = A2eiqx + B2e−iqx .

Поскольку отражённая от порога справа волна отсутствует (частицы падают на порог слева), то B2 = 0. Условие непрерывности Ψ1(0) = Ψ2 (0), Ψ1′(0) = Ψ2′(0) можно записать как

A1 + B2 = A2 , kA1 −qB1 = qA2.

Полагая A1 =1, получаем		k −q					2k
	B	k −q	,	A		=	2k	.	(10.27)
	B		,	A		=	k + q	.	(10.27)
Откуда	1 k + q			2			k + q
Откуда		k −q 2
R = B1 2	=	k −q 2		=	1− 1−U0 / E .
A 2		k + q			1+ 1−U0 / E
1

104

Отсюда следует, что при E >U0 существует отличная от нуля

вероятность того, что частица отразится от низкого потенциального порога, т.е. произойдет надбарьерное отражение – чисто квантовый эффект.

Вместе с тем с учётом формул (10.21) и (10.27)

D = A2 2	=	4kq	=	1−U0 / E
A1 2		(k + q)2		(1+ 1−U0 / E )2

и R + D =1.

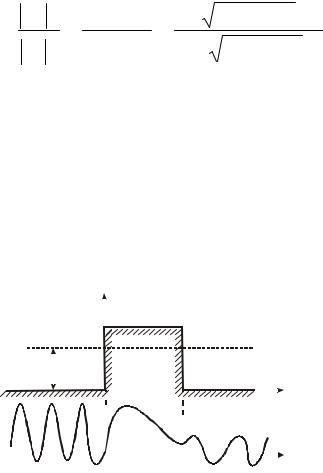
Рассмотрим ПБ простейшей формы для одномерного движения частицы (вдоль оси ОХ). Потенциальная кривая описывается системой

0, x ≤ 0,

U (x) = U0 , 0 < x < l,

0, x ≥ l.

Запишем УШ для областей 1, 2, 3, (рис. 10.6) соответственно:

Ψ3(х) x

Ψ1(х)

Ψ2(х)

Рис. 10.6

∂2Ψ

2Ψ = 0, k 2 =

2mE

(1)

1 + k

∂x2

Ψ2 + q2Ψ

= 0,

k 2

2m (E −U

(2)

∂

∂x2

∂2Ψ

2mE

(3)

3 + k 2Ψ = 0,

k 2

∂x

Функции Ψ1, Ψ2 , Ψ3 представляют собой одно и то же решение в

соответствующих интервалах изменения переменной х. Чтобы это решение было непрерывно вместе с первой производной необходимо выполнение граничных условий

105

Ψ1(0)	= Ψ2 (0),	и	Ψ2 (l) = Ψ3 (l),	(10.28)
Ψ1′(0)	= Ψ2′(0),		Ψ2′(l) = Ψ3′(l).
Запишем общее решение уравнений системы:

(1)Ψ		(x) = A eikx + B e−ikx ,
	1		1	1
(2)Ψ			(x) = A eiqx + B e−iqx		,	(10.29)
	2		2	2
(3)Ψ			(x) = A eikx + B e−ikx .
	3		3	3
	3		3	3

В областях 1 и 3 частица движется как свободная. Поэтому физический смысл выражений (слагаемых) A1eikx и A3eikx – волна, распространяющаяся

вдоль оси Ох соответственно в 1 и 3-й области, а B1e−ikx – волна, отражённая от ПБ, движущаяся против оси Ох. Так как в 3-й области отражённых волн нет, то В3 = 0.

Найдём коэффициенты A1, B1, B2 , A2					, A3 . Для этого решим совместно
системы (10.33) и (10.29):
Ψ1(0) = A1 + B1,Ψ2 (0) = A2 + B2 , так как Ψ1(0) = Ψ2 (0), то
			A1 + B1 = A2		+ B2 ;	(10.30)
Ψ (l) = A eiql + B e−iql			, Ψ (l) = A eikl , т.к. Ψ (l) = Ψ (l), то
2	2	2	3	3	2	3
		A eiql + B e−iql = A eikl .				(10.31)
		2		2	3

Найдём производные:

Ψ1′(0) = (A1eikxik + B1e−ikx (−ik))x=0 = ikA1 −ikB1 = ik(A1

аналогично Ψ2′(0) = iq(A2 − B2 ). Так как Ψ1′(0) = Ψ2′(0), то

k(A1 + B1) = q(A2 − B2 );

Ψ2′(l) = (A2eiqxiq + B2e−iqx (−iq)), Ψ3′(l) = A3eiklik , т.к. Ψ2′(l) iq(A2eiql − B2e−iql ) = ikA3eikl .

Окончательно получаем систему из (10.30)–(10.33):

A1 + B1 = A2 + B2 ,
A eiql + B				e−iql =	A eikl ,
	2	2			3
			q

		= k (A2 − B2 ),
A1 − B1		= k (A2 − B2 ),
						k
(A eiql		− B e−iql )			=	k	A eikl .
(A eiql		− B e−iql )			=	q	A eikl .
	2	2				q	3

− B1),

(10.32)

= Ψ3′(l), то

(10.33)

(10.34)

Сложим почленно первое и третье уравнения системы (10.34):

106

2A1 = A2 + B2 + qk A2 − qk B2 2A1 = (1+ kq)A2 +(1− qk )B2 . (10.35)

Сложим теперь почленно второе и четвёртое уравнения системы (10.34):

2A eiql = (1+	k		)A eikl A		=	1		A eikle−iql (1+			k	).	(10.36)
	q
2		3		2	2			3			q
Вычтем из второго четвёртое уравнение в системе (3.39):
2Вe−iql = (1−	k		)A eikl B		=		1	(1−	k	)A eikl eiql .			(10.37)

	q	3		2	2				q	3

Подставим выражения (10.36) и (10.37) в (10.35):

2A = (1+ q) 1

A eikle−iql (1+ k ) +

1 (1− q)(1− k )A eikleiql

A eikl

(1+

)(1+

)e−iql

+(1−

)(1−

)eiql

k + q

− q q

− k

A eikl

k + q

e−iql +

eiql

4kqA1 = A3eikl [(k + q)2 e−iql

−(k −q)2 eiql ];

4kqe−ikl

(k + q)2 e−iql −(k −q)2 eiql

(10.38)

Преобразуем знаменатель формулы (10.38) согласно формулам Эйлера

iϕ

= cosϕ +isinϕ ,

−iϕ

= cosϕ −isinϕ

или

cosϕ =

iϕ

+ e

−iϕ

) ,

sinϕ =

(eiϕ −e−iϕ )

(10.39)

После преобразований на основе (10.39) формула (10.38) примет вид:

2kqeikl

(10.40)

2kqcosql −i(k + q)2 sin ql

С учётом физического смысла формул (10.19), (10.20) и изменённого для

данного

случая равенства (10.21):

прош

формулы

для

коэффициентов отражения и прозрачности ПБ примут следующий вид:

	jотр		В	2		jпрош			А		2


R =		=	1		; D =		=	3
			1					3
	jпад		A	2		jпад			A	2


			1						1

с выполнением равенства (10.23). Проведём анализ формулы (10.40):

107

Пусть

E >U0 ,

тогда q =

(E −U0 )

– число действительное,

отсюда

= A A * = eikl e−ikl и

4k 2q2

D =

4k 2q

2 cos2 ql +(k 2

+ q2 )2 sin2 ql

Из равенства (10.23)

R =1− D =	(k 2 −q2 )2
		.
	(k 2 + q2 )2 + 4k 2q2ctg 2ql

Получаем неожиданный с точки зрения классической механики результат: частица имеет не равную нулю вероятность отразиться от барьера, несмотря на то, что её энергия превышает высоту ПБ.

2. Пусть теперь E <U0

, тогда

q =

(E −U

0 ) – число

мнимое.

Обозначим в формуле (10.36)

q = if , где f = 1

2m(U

0 − E) ,

4kife−ikl

(10.41)

+if )2 e fl −(k −if )2 e fl

Введём гиперболические функции (гиперболические синус и косинус):

shfl =

(e fl

−e− fl ),

chfl =

(e fl

+ e− fl ).

Формулу (10.41) можно переписать в виде

2ikfe−ikl

(k 2 − f

2 )shfl + 2ikfchfl

тогда

4k 2 f 2

D =

(10.42)

(k 2 − f 2 )sh2 fl + 4k 2 f 2ch2 fl

Замечателен вывод из этой формулы: даже если E <U0 , то есть энергия частицы ниже пика барьера U0 , то частица всё же может пройти через него.

На практике вместо громоздкой формулы (10.42) для приближённых оценок используют приближение при условии e2 fl >>1. Если это

108

неравенство справедливо, то shfl = chfl = 12 e fl и формула (10.42) примет вид

	16k	2	f	2	e−2 fl = D e	−	2	l 2m(U 0	−E)
D =										E <U
							h		,		0	. (10.43)

	(k 2 + f 2 )2				0

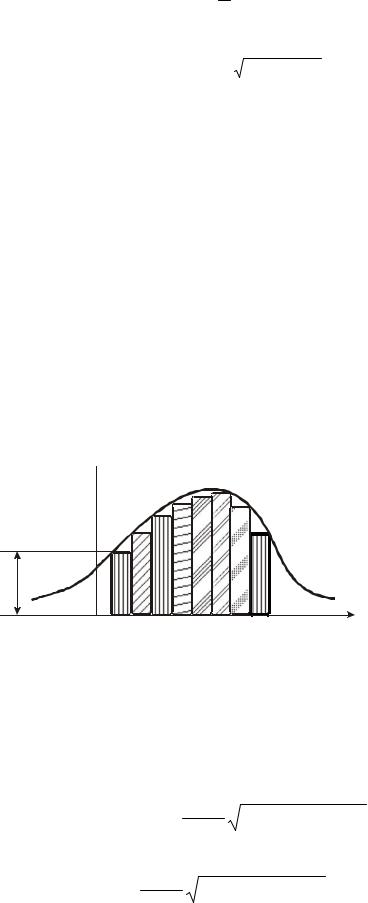
Из формулы (10.43) видно, что вероятность прохождения частицы через барьер тем меньше, чем шире и выше барьер. Характерно, что частица выходит за пределы ПБ с той же энергией, с которой входит в него. Поэтому явление прохождения частицы через барьер называется туннельным эффектом (частица не взбирается на вершину барьера, она как бы проходит под ним через туннель). Туннельный эффект – чисто квантовое явление, которое можно объяснить только с учётом волновых свойств частиц. Он лежит в основе многих физических явлений, например, автоэлектронной или холодной эмиссии электронов из металла. Обобщим полученный для прямоугольного ПБ результат на случай ПБ произвольной формы (рис. 10.7). Для этого представим ПБ в виде последовательности большого числа узких прямоугольных ПБ, расположенных один за другим. Будем считать, что барьер имеет достаточно плавную форму, то есть полагать, что его высота на расстоянии, сравнимом с длинной волны де Бройля, изменяется незначительно. Будем пренебрегать также надбарьерным отражением

частицы.

x1	x2	x
	Рис. 10.7

Волна де Бройля, прошедшая через i-й прямоугольный барьер, представляет собой волну, падающую на (i+1)-й ПБ и так далее.

Верность наступления цепочки взаимообусловленных событий (прохождения частицы через цепочку ПБ) равна произведению вероятностей (прохождения через каждый из барьеров):

	2∆x			=
D = ∏Di ≈ ∏exp −		i	2m(U (xi ) − E)	=
i	h


= exp − ∑2∆xi		2m(U (xi ) − E) ,
	h

109

где ∆xi – ширина i-го барьера, U (xi ) – его высота.

Переходя	в пределе ∆xi	→ 0		от суммирования к интегрированию,
получаем		2 x2
получаем	D = exp −		∫	2m(U (x) − E)dx .
		h	x1
			x1

10.4.Квантовый гармонический осциллятор

Вразделе ”Колебания” нашего курса давалось определение линейного гармонического осциллятора (ЛГО) – так называется модель системы, в которой происходят гармонические колебания, причем, с малыми по сравнению с размерами системы, амплитудами. То есть, возмущения, приводящие к таким колебаниям, также должны быть малы.

Маятник – простейший пример ЛГО. Сила, возникающая в системе с маятником при его возмущении и возвращающая его в положение равновесия, называется квазиупругой.

Второй закон Ньютона для колеблющегося тела можно записать в виде


	d	2	x
ma = m				= −kx , отсюда следует x+	k	x = 0 или x+ω2 x = 0.
	dt 2
					m
Это дифференциальное уравнение свободных незатухающих
гармонических колебаний. Общее его решение имеет вид:
				x(t) = Acos(ωt +ϕ0 ).			(10.44)

Осциллятор при условии (10.44) называется ЛГО. Потенциальная энергия для гармонических колебаний, например для пружинного маятника,

Wп =U = −∫Fxdx = F

= ma = m

= −Aω2sin(ωt +ϕ0 ) =ω2 x

dt 2

mω2 x2

(10.45)

U(x)

n=3

n=2

n=0

n=1

EE2

-x

max

Рис. 10.8

Рис. 10.9

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2811 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.09.2019351.74 Кб2Lab_01_New.doc
#
09.02.2015685.06 Кб3lab_excel_1.doc
#
09.02.2015294.61 Кб7Lab_rab_3.docx
#
09.02.2015422.61 Кб25Lab_rab_4_Fayly.docx
#
09.02.20151.89 Mб26lection_part1-2.pdf
#
09.02.20152.93 Mб20lection_part3.pdf
#
22.03.20163.28 Mб7Lecture 02.pdf
#
22.03.20162.59 Mб6Lecture 07.pdf
#
22.03.201613.56 Кб8lecture marketing.docx
#
22.03.20162.32 Mб45Lecture Notes on Solving Large Scale Eigenvalue Problems.pdf
#
22.03.20163.59 Mб6Lecture_01.pdf