
lection_part3
.pdf
n = |
m3 / 2 |
∞ |
|
EdE |
|
|
||||
|
2 |
|
3 ∫ |
|
|
|
|
. |
(14.8) |
|
2π |
h |
|
E −µ |
|
|
|||||
|
|
0 |
|
|
|
|
|
|
||
|
|
e kБT |
−1 |
|
|
|||||
|
|
|
|
|
|
|
||||
Из формулы (14.8) можно найти значение химпотенциала |
µ. Условие |
|||||||||
(14.8) может выполняться только при отрицательных значениях µ. Если предположить µ > 0, то подынтегральное выражение будет отрицательным,
что невозможно, так как функция распределения по смыслу связана с вероятностью и должна быть неотрицательной. Таким образом, µ ≤ 0 . В
связи с этим производные всегда отрицательны ∂µ / ∂T < 0 , т.е. можно сказать, что химпотенциал µ растет с уменьшением температуры Т, все время оставаясь отрицательной величиной. Химпотенциал µ обращается в
нуль при некоторой температуре Т0 ≠0 К. Обратившись в нуль при Т0 величина µ = 0 и при более низких температурах.
Чтобы выполнялось равенство (14.8), необходимо также предположить, что число частиц в системе уменьшается с уменьшением температуры, что, в свою очередь, невозможно, так как уйти из системы частицы не могут. Поэтому для выполнения равенства (14.8) частицы должны перейти на уровень с нулевой энергией, то есть при Т≤Т0 часть частиц должна находиться на уровне с нулевой энергией, а остальные будут распределены по другим уровням. Описанное явление называется бозе-конденсацией, при абсолютном нуле температуры все частицы бозе-газа будут находиться на нулевом уровне. В этом проявляется одно из свойств бозе-газа.
Оценка температуры конденсации показывает, что при этой температуре все вещества находятся либо в твердом, либо в жидком состояниях, то есть не являются газами, что подтверждается экспериментами. Например, для гелия He при Т≤2,19 К наблюдается своеобразное изменение состояния этого бозегаза. Жидкий гелий состоит при этом из двух компонент: несконденсированной и сконденсированной (сверхтекучей) частей бозе-газа. Обнаружение явления сверхтекучести рассматривается в качестве экспериментального подтверждения теории конденсации бозе-газа. По аналогии рассматривается и явление сверхпроводимости, когда при температурах, близких к абсолютному нулю, образуются бозоны – пары взаимосвязанных электронов – куперовские пары. К данному газу также применима теория бозе-конденсации.
Рассмотрим другие свойства бозе-газа. С учетом формулы (14.8) имеем
∞ |
m3 / 2 |
∞ E3 / 2dE |
|
|
||||||
E = ∫Ef (E)dN(E) = |
|
2 |
|
3 ∫ |
|
|
|
. |
(14.9) |
|
2π |
h |
E −µ |
|
|
||||||
0 |
|
0 |
|
|
|
|
|
|
||
|
e kБT |
−1 |
|
|
||||||
|
|
|
|
|
|
|
||||
171

Из курса общей физики (формула (9.18), лекция 9, часть I настоящего пособия) известно, что давление и энергия в единице объема связаны соотношением P = 2E /(3V ) (у нас объем единичный V=1 м3), тогда
P = |
2m3/ 2 ∞ E3/ 2dE |
|
|
|||||||||
|
2 |
|
|
3 |
∫ |
|
|
|
. |
(14.10) |
||
3π |
h |
E −µ |
|
|
||||||||
|
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
e kБT |
−1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
Покажем, что при выполнении условий |
|
|
|
|
||||||||
|
|
|
|
µ |
|
|
|
|
|
|
|
|
|
e |
kБT |
<<1 |
|
|
|
(14.11) |
|||||
|
|
|
|
|
, |
|
|
|
||||
|
|
|
|
>> µ |
|
|
|
|
|
|||
|
E |
|
|
|
|
|
||||||
Уравнение (14.10) переходит в уравнение Менделеева–Клапейрона, описывающего состояние идеального газа. Для этого воспользуемся малостью величины exp[µ /(kБT )]<<1. Обозначим E/(kБT)=х с учетом
∞ |
3 |
πα−3/ 2 , получим |
табличного интеграла ∫x3/ 2e−αxdx = |
||
0 |
4 |
|
|
|
µ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = |
2m3/ 2 (kБT )5 / 2 ∞ x3/ 2ekБT e−xdx |
= |
|||||||||||||||||
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
3π 2h3 |
|
|
|
µ |
|
|
|
|
|||||||||
|
|
|
|
|
0 1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
−ekБT e |
−x |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
14243 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≈0 |
|
|
|
|
||
= 2m |
3/ 2 |
(kБT ) |
5 / 2 |
|
µ |
∞ |
|
|
|
|
|
|
3/ 2 |
|
БT ) |
5 / 2 |
||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
ekБT ∫x3/ 2e−xdx = m |
|
|
|
(k |
|
|||||||||||||
|
3π 2h3 |
|
|
0 |
|
|
|
|
|
2 2π3/ 2h3 |
||||||||||
|
|
|
|
|
14243 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
=3 |
π / 4 |
|
|
|
|
|
|
|
|
|
|
|
|||
µ
ekБT . (14.12)
С учетом формулы (14.8) уравнение (14.12) должно принять вид уравнения Менделеева–Клапейрона. Для этого необходимо выполнить ряд преобразований. Во-первых, привести формулу (14.8) с учетом замены
∞ |
−αx |
|
π |
|
−3/ 2 |
|
|
E/(kБT)=х и табличного интеграла ∫ xe |
dx = |
α |
к виду |
||||
|
2 |
|
|||||
0 |
|
|
|
|
|
||
|
|
|
|
|
|
172
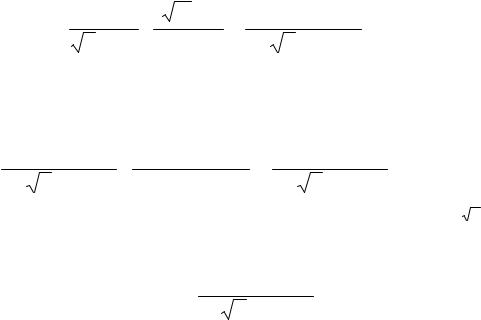
|
n = |
m3 / 2 |
∞ |
|
|
EdE |
= |
m3 / 2 (kБT )3 / 2 |
∞ |
|
x1/ 2dx |
= |
|
||||||||||||||||||||||||||||||
|
|
2 |
|
3 ∫ |
|
E −µ |
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|||||||||||
|
2π |
h |
|
|
|
|
|
|
|
|
|
|
2π |
h |
|
|
|
|
µ |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
e kБT −1 |
|
|
|
|
|
|
|
|
|
|
|
|
ekБT e |
−x |
−1 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
123 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≈0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
m3 / 2 |
(k |
|
T )3 / 2 ∞ x1/ 2ekБT e−xdx |
|
|
|
|
m3 / 2 |
(k |
|
T )3 / 2 |
|
|
∞ |
1/ 2 |
|
−x |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
= |
Б |
= |
Б |
e |
k |
T |
|
e |
dx = |
||||||||||||||||||||||||||||||||||
|
|
|
|
∫ |
|
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
∫ x |
|
||||||||||||||||
|
|
2π 2h3 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2π 2h3 |
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||
|
|
|
1−ekБT e−x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14243 |
|||||||||||||||
|
|
|
|
|
|
|
|
123 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= π / 2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
≈0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
m3 / 2 (k |
|
|
T )3 / 2 |
|
|
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
= |
Б |
|
e |
k |
|
T |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(14.13) |
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2π3 / 2h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Сравнивая формулы (14.13) и (14.12), можно записать уравнение |
|||||||||||||||||||||||||||||||||||||||||||
Менделеева–Клапейрона в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = nkБT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(14.14) |
|||||||
или для произвольного числа молей в более привычном виде |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PV = |
|
m |
RT . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(14.15) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, при выполнении условий (14.11) (энергия частицы много больше химпотенциала) квантовая статистика Бозе–Эйнштейна переходит в классическую статистику Максвелла–Больцмана. При этом возможно получение уравнений классической физики из более общих – квантовых – уравнений.
По аналогии с проведенным выше рассмотрением для бозе-газа
рассмотрим применение квантовой статистики Ферми–Дирака к системе частиц с полуцелым спином с учетом принципа запрета Паули. Такими частицами являются фермионы: электроны, µ-мезоны, нуклоны, а также
атомы, в которых число электронов и нуклонов является нечетным. Такую систему можно рассматривать как ферми-газ, описываемый функцией распределения вида (14.3)
f (E) = |
1 |
|
. |
(14.16) |
|
|
E −µ |
|
|||
|
e kБT |
+1 |
|
||
173
Рассматривая невзаимодействующие частицы в пространстве импульсов, для числа состояний с энергией в интервале [E; E+dE] в единице объема конфигураций (у нас объем единичный V=1 м3) можно по аналогии с выводом формулы (14.7) получить
dN (E) = |
2m3 / 2 E1/ 2dE |
. |
(14.18) |
|
2π 2h3 |
||||
|
|
|
Множитель «2» перед формулой записан с учетом того, что в состоянии с одинаковой энергией могут находиться только два фермиона с противоположными спинами (g(E)=2 согласно принципу запрета Паули).
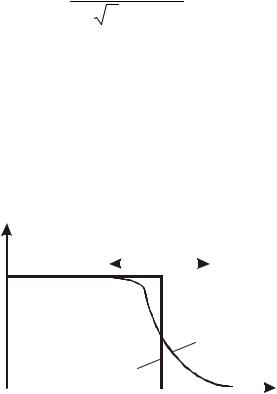
При рассмотрении свойств ферми-газа интерес представляет график зависимости функции распределения Ферми–Дирака от термодинамической температуры и энергии (рис. 14.2).
|
|
f(E) |
|
|
|
|
|
|
|
~kБT |
|
|
|
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T>0K |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
T=0K |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E0=µ |
E |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 14.2 |
|
|
|
||||||||||||
Отметим несколько ключевых моментов: |
|
|
|
|||||||||||||||||||||||
1) при |
µ /(kБT ) >>1 |
|
(тогда |
exp[− µ /(kБT )]≈ 0) |
и Е=0 |
|||||||||||||||||||||
f (E) = |
|
1 |
|
|
|
≈1; |
это означает, что |
пока энергия |
Е много |
|||||||||||||||||
|
E − µ |
|
+1 |
|||||||||||||||||||||||
|
exp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
kБT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
меньше химпотенциала µ (E<< µ), функция распределения f(E) ≈1; |
|
|||||||||||||||||||||||||
2) при E = µ имеем |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
||||||||||
f (E) = |
|
|
= |
|
. |
|
|
|
|
|||||||||||||||||
exp[0]+1 |
2 |
|
|
|
|
|||||||||||||||||||||
В данном случае следует рассказать о таком понятии, как энергия Ферми. При Т=0 К электроны в металле заполняют энергетические уровни, верхний из них и обладает энергией Ферми. Энергия Ферми – это максимально
174
большая энергия, которой обладает электрон в кристалле при температуре 0 К. С точки зрения статистической физики f(E)=1/2 означает, что вероятность заполнения энергетического уровня с энергией Ферми E0= µ при любой
температуре равна 1/2.
3)с дальнейшим ростом энергии Е функция распределения f(E) убывает
ипри E>> µ>>kБT убывание это становится близким к обычному
|
f (E) = |
|
1 |
|
|
|
|
µ − E |
|
|
экспоненциальному |
|
|
|
|
≈ exp |
|
(получаем |
|||
E − µ |
|
|
kБT |
|||||||
|
|
+1 |
|
|
|
|||||
|
|
exp |
|
|
|
|
|
|
||
|
|
kБT |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
функцию распределения Максвелла–Больцмана).
Функция распределения Ферми–Дирака для Т=0 К и Т>0 К заметно отличается лишь в небольшой области энергий порядка kБT.
14.3. Применение методов статистической физики к равновесному (тепловому) излучению
(перед изучением данного материала необходимо ознакомиться с лекцией 7, ч. III данного пособия)
Рассматривается равновесное – тепловое – излучение: сколько энергии в единичном интервале частот в единицу времени излучается, столько же и поглощается. Данное излучение можно представить с использованием модели стоячей волны. По аналогии с выбором фазовой ячейки и вычислении числа состояний с импульсом р в данной ячейке (формула (14.6)) удобно выбрать за основу число стоячих волн, имеющих частоту того или иного бесконечно малого участка спектра
dN (v) = 2 |
4πv2dv |
= |
8πv2dv |
, |
(14.19) |
|
c3 |
c3 |
|||||
|
|
|
|
|||
при этом использовалось известное соотношение |
|
p = h / λ = hv / c , где с – |
||||
скорость света в вакууме, а множитель «2» перед формулой связан с возможностью поляризации волны в двух взаимноперпендикулярных направлениях.
Задача в данном случае сводится к нахождению распределения энергии по частотам в спектре излучения АЧТ по известному распределению числа ЭМВ (14.19).
Так как стоячая волна может рассматриваться как одна колебательная степень свободы, то ее средняя энергия < ε >= 2 1/ 2 kБT = kБT . С учетом
этого английские физики Р.Дж.У.Рэлей (1842–1919) и Дж.Х.Джинс (1877– 1946) независимо друг от друга в 1900 году была получили формулу Рэлея–
175

Джинса (7.7). Опыт показывает, что формула (7.7) справедлива в области малых частот v (больших длин волн λ) и высоких температур Т. Попытка получить из формулы (7.7) закон Стефана–Больцмана (7.5) получила название «ультрафиолетовой катастрофы» (7.8), хотя согласно формуле
(7.5) RTАЧТ ~ T 4 . Сильное расхождение наблюдалось в коротковолновом
спектре (см. рис. 7.1). Подобная неудача объясняется неверным выражением для средней энергии гармонического осциллятора – колеблющихся в узлах кристаллической решетки атомов АЧТ.
В области больших частот v хорошее согласие с опытом давал закон излучения Вина
r |
= C v3 A exp[− Av /T ], |
(14.20) |
v,T |
|
|
где С и А – некоторые константы.
Верное выражение для средней энергии гармонического осциллятора с собственной частотой v и, следовательно, для rv,T было получено в 1900 году
немецким физиком–теоретиком М.К.Э.Л.Планком (1858–1947) на базе его квантовой гипотезы. Согласно квантовой гипотезе Планка свет излучается порциями – квантами с энергией каждого кванта E = hv , где
h = 6,63 10−34 Дж с – постоянная Планка. Таким образом, ТИ можно рассматривать как поток квантов – фотонов. С учетом статистических закономерностей при рассмотрении такого квантового коллектива частиц (фотонов) М.Планк 14 декабря 1900 года на заседании Берлинского физического общества продемонстрировал вывод формулы (7.9). 14 декабря
1900 года считается днем рождения новой – квантовой физики, а формула (7.9), хорошо согласующаяся с опытом, получила название
«закон излучения Планка». Из формулы (7.9) могут быть получены все выше рассмотренные частные случаи (законы) (7.5)– (7.7).
Представим равновесное излучение как газ невзаимодействующих частиц с целым спином – фотонов с энергией E=hv. Число частиц в таком газе есть переменная величина, зависящая от объема и температуры
< n(E) >= |
1 |
= |
1 |
. |
(14.21) |
E |
|
||||
|
|
hv |
|
||
ekБT −1 ekБT −1
Данное выражение справедливо для равновесного излучения при µ = 0
(см. формулу (14.4)). Число фотонов различной поляризации в фазовой ячейке в единичном объеме пространства конфигураций V=1 м3 определяется выражением (14.19). Тогда энергия равновесного излучения, приходящаяся на интервал спектра частот [v; v+dv]
176
dE(v) = hv dN(v) < n(E) >= |
|
8πhv3dv |
|
(14.22) |
||||
|
|
|
|
hv |
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
kБT |
|
|
||
|
c |
3 |
|
e |
−1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
(можно сравнить формулу (14.22) с формулой М.Планка (7.9)).
Считая распределение по частоте непрерывным, можно вычислить полную энергию фотонного газа для единицы объема с учетом табличного
∞ |
x3 |
dx = |
π 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
интеграла ∫ |
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 ex −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hv |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
∞ |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
8πh |
|
v |
dv |
= kБT |
|||||||||||||
|
U = |
∫dE(v) = |
∫ |
|
|
|||||||||||||||||||
|
|
|
|
hv |
|
|
||||||||||||||||||
|
|
|
|
0 |
|
|
|
c3 |
0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
e |
kБT |
|
|
dv = |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
8πh k |
|
T ∞ |
x3dx |
|
|
|
|
8π5k 4 |
T |
4 |
||||||||||
|
|
|
= |
|
|
Б |
|
|
|
|
|
|
|
|
= |
|
|
Б |
|
|
||||
|
|
|
|
|
|
|
|
−1 |
15c3h3 |
|
|
|||||||||||||
|
|
|
|
c3 |
h 0∫ ex |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
123 |
|
|
|
|
|
|
|
|
|
|
|
|||||
= x, |
|
|
|
||
|
|
|
|||
k |
|
T |
|
|
= |
Б |
|
|
|
||
|
|
dx |
|
||
|
h |
|
|
|
|
=σT 4 , |
|
(14.23) |
|||
|
8π5k 4 |
=π 4 /15 |
|
где σ = |
– постоянная Стефана–Больцмана (см. закон Стефана– |
||
Б |
|||
|
15c3h3 |
|
Больцмана (7.5)).
177
Лекция 15. Элементы физики твердого тела – II
1.Теплоемкость твердых тел. Электронный газ в металлах. Понятие о квантовой теории электро- и теплопроводности металлов. Явление сверхпроводимости.
2.Решение уравнения Э.Шредингера для твердого тела. Понятие о зонной теории твердых тел. Металлы, полупроводники и диэлектрики. Их электрические свойства.
15.1.Теплоемкость твердых тел. Электронный газ в металлах. Понятие о
квантовой теории электро- и теплопроводности металлов. Явление сверхпроводимости
(перед изучением данного материала следует ознакомиться с вопросом 11.2, лекция 11, ч. I и вопросом 7.2, лекция 7, ч. II настоящего пособия)
В 1819 году французские физики П.Л.Дюлонг (1785–1838) и А.Т.Пти (1791–1820) экспериментально установили закон, согласно которому молярная теплоемкость (в отличие от удельной) химически простого одноатомного вещества при больших температурах (комнатная и выше) равна 3R, где R=8,31 Дж/(моль К) – универсальная газовая постоянная
CV=3R≈25 Дж/(моль К). |
(15.1) |
Формула (15.1) называется законом Дюлонга–Пти. |
|
Для молярной теплоемкости органических соединений справедлив закон |
|
Неймана–Коппа (1864 г.), согласно которому |
|
CV=3nR, |
(15.2) |
где n – число атомов в соединении. |
|
Закон Дюлонга–Пти достаточно легко объясним |
с помощью |
классической физики. Например, в 1 моле вещества содержится NA частиц, данному твердому телу (ТТ) можно поставить в соответствие 3NA гармонических осцилляторов (три взаимноперпендикулярных направления колебаний – три степени свободы). Тогда энергия теплового движения
E=3NA<ε >, где <ε > – средняя энергия одного осциллятора. В классической физике энергия считается равномерно распределенной по степеням свободы, каждой степени свободы соответствует энергия kБT/2. Энергия гармонического осциллятора складывается из примерно равных потенциальной и кинетической энергий, т.е. <ε >=kБT. Тогда E=3NAkБT=RT, а по определению теплоемкости
CV = (dE / dT )V |
(15.3) |
легко получаем формулу (15.1).
Закон (15.2) справедлив в отсутствие свободных электронов в ТТ, т.е. когда ТТ является диэлектриком. В металлах в тепловом движении участвуют не только атомы (колебательное движение), но и электроны (поступательное движение). Свободные электроны имеют 3 степени свободы, т.е. средняя энергия электрона 3kБT/2. Если валентность атома Z, то полная энергия теплового движения для 1 моля металла складывается из двух слагаемых:
178
первое выражает энергию осцилляторов–атомов в узлах кристаллической решетки, а второе выражает энергию электронного газа в металле
E=3NA kБT+ 3ZNAkБT/2=3RNA(1+Z/2). (15.4)
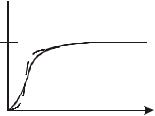
По определению теплоемкости (15.3) даже для одновалентного металла (Z=1) молярная теплоемкость CV=4,5R, что в 1,5 раза больше опытной, выражаемой формулой (15.2). Данная ситуация получила название «катастрофа с теплоемкостью». Вклад электронов в теплоемкость классическая теория объяснить не смогла, ее выводы ограниченно применимы. Делалась попытка объяснить участие электронов в формирование теплоемкости в теории А.Эйнштейна (1907 г.), а затем П.Дебая (1912 г.). Теория Эйнштейна не дала согласия с опытом в области низких температур (рис. 15.1, данные
теории Эйнштейна – пунктир, опыт – сплошная линия).
CV 
3R
T, K
Рис. 15.1
Теория Дебая, также являясь из-за ряда допущений приближенной, при расчете на ЭВМ дает достаточно хорошее согласие с опытом практически для всех температур. Дальнейшее рассмотрение для спорного случая – для низких температур будем проводить согласно теории П.Дебая.
Фононом называется элементарная порция (квант) звуковой энергии с частотой ω и энергией ε = hω , подобно тому, как фотон – квант электромагнитного излучения. И фонон, и фотон являются бозонами. Это означает, что все соотношения, полученные в предыдущей лекции для фотонов, останутся верными и для фононов. Звуковые фононы полностью аналогичны фотонам, ибо и те, и другие описываются одним и тем же законом дисперсии: для фотонов ω = ck , а для звуковых фононов ω = sk , где k – волновое число, с – скорость света в вакууме, s – скорость звука. Степень вырождения (состояния) у фотонов 2 (два взаимноперпендикулярных направления поляризации), а у фонона 3 (в твердом теле (ТТ) звуковые волны могут быть продольными и поперечными, причем имеются две независимые поперечные поляризации). Фотоны могут иметь любую частоту от 0 до ∞, а фононы имеют верхнее ограничение.
Используя формулу (14.22) с заменой h = h /(2π), скорости света с на
среднюю скорость звука s, v на ω = 2πv , для энергии единицы объема кристалла при заданной температуре Т получим
179
E |
= |
3h |
|
ωmax |
|
ω3dω |
|
|
|
|
|||||
V |
|
|
|
∫ |
|
|
|
|
|
|
. |
(15.5) |
|||
π 2 |
s |
3 |
|
|
hω |
|
|
|
|||||||
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
e |
k |
Б |
T |
− |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисляя интеграл (15.5) аналогично интегралу (14.22), см. переход к формуле (14.23), для энергии единичного объема имеем
E = |
|
π 2k |
4 |
T 4 . |
|
|
|
|
Б |
(15.6) |
|||
10h3s3 |
||||||
|
|
|
||||
По определению теплоемкости (15.3)
|
2π 2k 4 |
|
|
C = dE / dT = |
Б |
T 3 . |
(15.7) |
|
|||
V |
5h3s3 |
|
|
|
|
||
Формула (15.3) называется законом Дебая для низкотемпературной теплоемкости, согласно ей CV~T3, что для низких температур согласуется с опытом (рис. 15.1).
В теории Дебая вводится понятие характеристической температуры Дебая, соответствующей максимальной частоте колебаний атомов в узлах кристаллической решетки и, следовательно, максимальной энергии фононов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6π 2 N A s3h3 1/ 3 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
Θ |
Д |
|
= (hω |
max |
) / k |
Б |
= |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
(15.8) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VkБ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Интеграл |
|
энергии |
|
(15.5) |
|
|
в |
|
|
|
теории |
Дебая |
|
с |
|
помощью |
|
замен |
||||||||||||||||||||||||||||||
hω /(kБT ) = x ω = kБTx / h, |
|
dω = kБTdx / h, |
|
xmax = hωmax /(kБT ) , |
||||||||||||||||||||||||||||||||||||||||||||
ΘД = (hωmax ) / kБ приводится к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
E = |
|
3Vh |
ω |
max |
|
|
ω |
3 |
dω |
|
|
|
|
|
|
|
3Vh |
|
k |
Б |
T |
|
4 x |
max |
x |
3 |
dx |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
= |
|||||||
2π 2 s3 |
|
|
|
|
|
hω |
|
|
|
|
2π 2 s3 |
|
|
|
|
|
ex |
|
−1 |
|||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
h |
|
|
0 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e kБT |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 ΘД /T x3dx |
|
|
||||||||||||||
|
N |
A |
k |
Б |
|
9k 3 |
|
|
|
|
|
|
xmax |
x3dx |
|
|
|
|
T |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
Б |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
N A |
|
|
6π |
2 |
s |
3 |
h |
3 T |
|
|
|
∫ |
|
e |
x |
−1 |
|
= 9RT |
|
|
|
|
|
∫ |
|
e |
x |
|
|
= |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
ΘД |
|
|
0 |
|
|
|
−1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 3RT D(T / ΘД ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
(15.9) |
||||||||||||||||||||
Именно в формуле (15.9) и задается характеристическая температура Дебая, выражаемая формулой (15.8), а функция
|
T |
3 ΘД /T |
x |
3 |
dx |
|
|
|||
|
|
|
|
|
|
|||||
D(T / ΘД ) = 3 |
|
|
∫ |
|
|
|
|
=, |
(15.10) |
|
|
e |
x |
−1 |
|||||||
|
ΘД |
0 |
|
|
|
|
||||
180
