lection_part3

которую нельзя вычислить аналитически (ее значения вычисляются численными методами и приводятся обычно в таблицах), называется

теплоемкость согласно формуле (15.7) ~T3, что также согласуется с опытом. Результаты теории плохо согласуются с опытом при T = ΘД из-за

взятой П.Дебаем упрощенной – линейной – зависимости ω от волнового числа (вектора). Однако при подстановке в формулы Дебая данной реальной

– нелинейной – зависимости расчет с помощью ЭВМ также приводит к верным результатам, согласующимся с опытом.

Неудача описания явления теплопроводности металлов также обусловлена либо неучетом электронного газа в металлах в классической – газокинетической – физике, либо неверное рассмотрение поведения этого газа. Например, в классической электро- и теплопроводности металлов теории П.Друде предполагается одновременность столкновений свободных электронов с ионами решетки. В более поздней теории Лоренца последовал отказ от одновременности столкновений, но не было учета поведения электронов как фермионов, т.е. того, что сейчас мы знаем как принцип запрета В.Паули. Учет этого принципа вкупе с применением функции распределения электронов по энергиям (правда, равновесной функции распределения) в теории (1927г.) немецкого физика и математика А.Зоммерфельда (1868–1951) привел к результатам, согласующимся с опытом.

В классической теории Лоренца соответственно для удельных теплопроводности и проводимости получаются выражения

181

где kБ – постоянная Больцмана, τ – среднее время пробега между двумя последовательными столкновениями, n – концентрация электронов, me – масса электронов, Т – температура, CV – теплоемкость, v – средняя скорость электронов, е – модуль заряда электрона.

В квантовой теории А.Зоммерфельда при учете поведения (вклада) электронного газа получаются следующие соответствующие выражения

Видно, что формулы (15.12) и (15.14) совпадают по виду, но получены при кардинально различающихся подходах.

Согласно классической теории электро- и теплопроводности металлов носителями тока и теплоты (высокая теплопроводность металлов) являются свободные электроны. Г.Видеманом (1826–1899) и Францем в 1853 г. экспериментально установлено, что отношение теплопроводности χ к

удельной проводимости γ при данной температуре T есть величина

постоянная – закон Видемана–Франца (формула (7.11), ч. II данного пособия):

15.2. Решение уравнения Э.Шредингера для твердого тела. Понятие о зонной теории твердых тел. Металлы, полупроводники и диэлектрики.

Их электрические свойства

Известно, что твердое тело (ТТ) состоит из атомов, т.е. из ядер атомов и электронов. Ядра занимают положение, совпадающее с положением узлов кристаллической решётки, и совершают малые колебания у данного положения равновесия. Силы взаимодействия между ядрами велики, поэтому внешние силы для деформации кристалла должны быть значительны. Слабее всего с ядрами связаны внешние – валентные электроны, поэтому под действием внешнего поля (по большей части) они могут двигаться поступательно и участвовать в формировании электрического тока.

Для количественной характеристики данного процесса необходимо решать уравнение Шредингера (УШ) для системы очень большого числа частиц (вспомним NA=6,022 1023 моль–1), что в настоящее время напрямую

182

невозможно (даже для системы трёх взаимодействующих частей решение УШ сложно).

Поэтому для решения УШ для ТТ используют различные приближения:

+Vz (R1,..., RN ) +U (rr1,...rrn , R1,..., RN )]Ψ(rr1,...rrn , R1,..., RN ) =

14243 144424443

А. Так как масса ядер тя >> те и ядра в основном колеблются около положения равновесия, а электроны движутся в основном поступательно, то скорость Vя <<Vэл, что при малых смещениях ядер приводит к быстрому

перераспределению электронов. Отсюда можно утверждать, что изменение энергий и волновых функций электронов происходит практически без энергообмена с ядрами. Данное приближение называется адиабатическим (приближение Борна–Оппенгеймера): электроны движутся в поле практически фиксированных ядер, при этом координаты ядер входят как параметры в выражения для Е и Ψ электронов (а не как переменные).

Самое грубое адиабатическое приближение – когда ядра неподвижны,

их кинетическая энергия равна нулю, т.е. электроны движутся в постоянном периодическом поле ядер, при этом энергия взаимодействия ядер между

собой будет константой (V0 ). Соответствующим подбором нулевого уровня можно добиться того, что V0 = 0 , тогда в уравнении (15.16) останутся только

первое, третье, и пятое слагаемые.

Б. Ещё одним приближением, упрощающим решение УШ для ТТ,

является приближение самосогласованного поля (Хартри–Фока): поле всех электронов, определяющее движение каждого электрона, в свою очередь, определяется и им. В данном приближении третье слагаемое в уравнении (15.16) будет иметь вид суммы функций

∑Wi (rri). (15.17)

i

Пятое слагаемое в уравнении (15.16) также можно упростить, представив в виде суммы энергий взаимодействия каждого электрона с полем всех ядер, являющимся для электронов определяющим (электроны же практически не влияют на ядра):

183

состояния данного электрона и не зависят от состояния других электронов, т.е. можно записать без индексов

Трудности решения уравнения (15.20) заключается в определении вида функции V (r ) . Используются различные приближения, т.к. вид V (r ) строго

не определяется ни теоретически, ни практически.

Данные приближения: метод псевдопотенциалов, метод плоских волн, метод функции Грина и так далее, однако качественные результаты (без ЭВМ) можно получить уже в приближении для функции V (r ) в уравнении

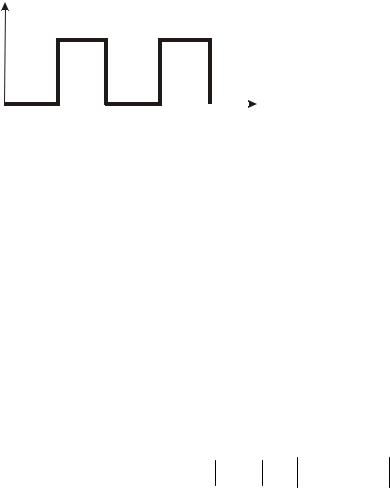
(15.20), называемом моделью Кронига – Пенни: функция V (rr)

представляет собой набор чередующихся потенциальных ям шириной а и потенциальных барьеров шириной b и высотой V0 :

184

Ранее уже указывались требования, налагаемые на ВФ частиц. Однако для электрона в кристалле необходимо учитывать ещё и пространственную периодичность, т.е. учитывать особенности строения кристалла.

В каждом кристалле можно выделить малую область, содержащую все особенности строения (симметрии) данного кристаллического вещества. При перемещении на некоторое расстояние (индивидуальное для каждого вещества) – трансляции – этой элементарной ячейки можно получить весь кристалл целиком (в идеале без дефектов).

Если RT – вектор трансляции, то свойства электрона должны быть

одинаковыми при его координате r и rr+ RT , т.е.

Ψ(rr) 2 = Ψ(rr+ RrT ) 2 .

Это возможно (так как потенциальная энергия электрона в кристалле в силу периодичности U (rr) =U (rr+ RT ) ), если эти две функции отличаются

Функции (15.23) – функции Ф.Блоха (волны Блоха). Теорема Блоха:

ВФ электрона в кристалле представляет собой плоскую бегущую волну, модулированную по амплитуде периодической функцией ϕk (rr) , имеющей

период решётки.

Таким образом, решение (15.22) будем искать в виде функций Блоха

(15.23). Тогда

Ψ(х) =ϕ(х)eikx ,

Ψ′′(x) = (ϕ′(x)eikx +ϕ(x)ikeikx )/ =

=ϕ′′(x)eikx +ϕ′(x)ikeik x +ϕ′(x)ikeikx − k 2ϕ(x)eikx .

Подставляя все это в (15.22) и деля обе части на eikx , получаем

185

− h2 (ϕ′′+ 2ikxϕ′−k 2ϕ) +V (x)ϕ = Eϕ .

2m

При нахождении электрона в ПЯ (см. систему (15.21)):

Если электрон находится в области барьеров (см. систему (15.21)):

Решения для уравнений (15.24) и (15.26) соответственно будем искать в виде

Для определения констант А, В, С, D используем налагаемые на ВФ условия её непрерывности и непрерывности её производных на границе смежных областей (яма–барьер):

ϕ1 =ϕ2ϕ1′ =ϕ2′

Подставив соотношения (15.27), (15.28) в (15.29), получаем систему из четырёх линейных однородных уравнений относительно коэффициентов А, В, С, D. Условием существования нетривиального решения системы является равенство нулю детерминанта (определителя), составленного из коэффициентов при искомых величинах А, В, С, D.

После преобразований получаем уравнение

186

k = f (α, β) = f (E), можно получить представление об энергетическом

спектре электрона в кристалле. Прямое решение уравнения (15.30) вызывает очень большие трудности, поэтому сделаем ряд упрощений, следуя Кронигу

и Пенни. Рассмотрим очень тонкие (b → 0) и высокие (V0 → ∞) барьеры, но при этом так, чтобы величина bV0 была конечной. Это означает, что

Данный параметр определяет эффективную площадь каждого барьера, а также степень его прозрачности для электрона, степень связанности

свободного электрона.

187

2. При Q→ ∞ получаем приближение сильной связи или бесконечно глубокой потенциальной ямы, для которой, как мы знаем,

энергетических уровнях и поэтому слабо взаимодействующему с соседними атомами.

Данное приближение не соответствует валентным, наиболее слабо связанным с ядром электронам, которые будут взаимодействовать с соседними атомами. Нужна более строгая (зонная) теория. Поэтому для проведения качественного анализа необходимо наложить условие Q>>1 (должно быть большим, но конечным), но при этом αa должно слабо отличаться от πn (см. равенство (15.29)), т.е. должно быть

Подставляя разложения (15.35) и (15.36) в формулу (15.32), получим

части в квадрат, имеем

188

С учётом α2 = 2mE / h2 из уравнения (15.38) получаем приближенное выражение для энергии электрона в кристалле:

E0n – энергия электронов на n-м уровне изолированного атома; с образованием кристалла энергия электронов понижается (см. формулу (15.39)), что говорит о том, что образование кристалла энергетически выгодно. Последнее слагаемое определяет пределы изменения энергии электронов на n-ом уровне, т.е. определяет зонный характер энергетического спектра электрона в кристалле, E=f(k).

Согласно более строгому рассмотрению в зонной теории, при сближении атомов для образования кристаллической решётки происходит расщепление дискретных уровней энергии электронов свободных атомов в зоны разрешенных значений энергии, которые разделены зонами запрещённых значений энергии. В пределах зон уровни разрешённых значений энергии располагаются очень близко (разность энергий <0,1 эВ), поэтому в пределах зоны энергетический спектр можно считать

квазинепрерывным.

Верхнюю (последнюю) из заполненных разрешённых зон называют валентной зоной (ВЗ), а следующую за ней зону запрещённых значений энергии – запрещенной зоной (ЗЗ), а следующую свободную разрешённую –

зоной проводимости (ЗП).

Наиболее сильно расщепляются в зоны энергетические уровни валентных электронов свободных атомов (внешние электроны). Именно валентные (внешние) электроны в ВЗ определяют электропроводность, например, металлов, для которых не полностью заполненная ВЗ является и зоной проводимости. При наложении даже слабого электрического поля на кристалл электроны ВЗ могут ускоряться электрическим полем, приобретать

189

дополнительную скорость, т.е. кинетическую энергию, и переходят на более высокие уровни энергии в ВЗ, которые в данном случае свободны.

Электроны ВЗ могут участвовать в электропроводности даже при абсолютном нуле. К металлам (проводникам I рода) относятся вещества, у которых ВЗ либо не полностью заполнена электронами (и является ЗП), либо полностью заполнена, но перекрывается с ЗП, т.е. ширина ЗЗ Eg=0 (gap – англ. скачок, разрыв).

Полупроводниками являются кристаллы, у которых при абсолютном нуле температуры Т=0 К ВЗ полностью заполнена электронами, ЗП пуста, а

ширина ЗЗ Еg ≤ 3 эВ. Название «полупроводники» связано с тем

обстоятельством, что их удельная электропроводность при комнатных температурах имеет промежуточные значения между удельной электропроводностью металлов γ ~106–108 Ом м-1 и диэлектриков γ ~10-10–

10-8 Ом м-1. Характерной особенностью полупроводников является экспоненциальное возрастание γ =f(T) от температуры:

вотличие от металлов, для которых γ уменьшается (удельное сопротивление

ρ= ρ0 (1+αt) растёт линейно с ростом температуры, α =1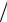273,15 град-1).

Полупроводники делят на прямозонные (центральные максимумы ЗП и ВЗ друг против друга) и непрямозонные (максимумы смещены друг относительно друга) в силу нелинейной зависимости изменения Ec (дно ЗП) (рис. 15.3, а) и Ev (потолок ВЗ) (рис. 15.3, б).

Рис. 15.3

Диэлектриками называются кристаллы, для которых выполняются условия для полупроводников, но Еg ≤ 2 −3 эВ. Электропроводность

диэлектриков возможна только при температурах, больших температуры их плавления; в обычных условиях диэлектрики электрический ток не проводят.

Таким образом, различие между металлами и диэлектриками

качественное, а между полупроводниками и диэлектриками количественное.

190