9.5 Рамки экспериментов с моделью.

Структура имитационной модели гомоморфна структуре изучаемой системы (основное требование).

6. Модели локальных механизмов.

При разработке имитационной модели в качестве элементов её структуры могут использоваться компоненты, представляющие собой аксиоматические, эмпирико-статистические, оптимизационные, эвристические, феноменологические модели. Все они описывают локальные внутрисистемные механизмы, имеют объективный характер и получаются в рамках конкретных дисциплин.

6. Структура и компоненты модели.

В структуре создаваемой имитационной модели отображаются представления её разработчиков о:

 проблеме в целом и способах её исследования;

 назначении модели и её ценности;

 действующих в системе функционально-целевых и причинных отношениях;

 взаимодействии системы с внешней средой.

6. Модель как выполняемая компьютерная программа.

Численные и тем более аналитические методы решений к имитационным моделям неприменимы. Они заменяются "вычислительными прогонами". В каждом прогоне изменение состояний модели обусловлено изменениями значений параметра имитации.

6. Непрерывная и дискретная имитация.

При прогонах во времени (траекторная генерация поведения) время изменяется необратимо и однонаправленно от начального к конечному значению на заданном интервале. Основными механизмами продвижения времени являются методы "конечного шага" и "шага до ближайшего состояния".

9. Системный подход (понятие)

Применяется при разработке контекстов проблем и их концептуальных моделей. Будучи продуктом системного подхода, концептуальные модели служат основой для построения моделей системного анализа. Применение системного анализа связано с обязательной формализацией концептуальных моделей.

9. Системный анализ (понятие)

Применяется при решении задач целостного описания и многоаспектного целенаправленного исследования контекстов прикладных проблем. На этапе системного анализа всякая решаемая задача должна быть сформулирована как задача математическая.

Лекция 2. Динамические системы (введение)

1. Линейный осциллятор

Осцилля́тор (от лат. oscillo — качаюсь) — система, совершающая колебания, то есть показатели которой периодически повторяются во времени.

1. Составление уравнения маятника второго порядка.

Составление уравнения маятника второго порядка:

Fтр=r*x’

Fупр=k*x

Fн=m*x’’

Fтр+Fупр+Fн=0

mx’’+rx’+kx=0 –уравнение маятника(делим наm) и получаем:

x’’+bx’+cx=0

л^2+b*л+с=0 –характеристическое уравнение

2. Особые точки и траектории движения в пространстве параметров линейного осциллятора второго порядка.

D=b^2-4c

D>0;л1,л2 – вещественные

D<0;л1,л2 – комплексно-сопряженные

D=0;л1,л2 – кратные вещественные

3. Получение характеристического уравнения.

Выше выведено

4. Определение особых точек. Типы особых точек. Свойства особых точек.

Особые точки: Узел (устойчивые, неустойчивый) - действительные корни Фокус(устойчивые, неустойчивый) – коплексно-сопряженные корни Центр – мнимые Седло – одно положителное, другое - отрицательный

1. Представление системы в: пространстве параметров; фазовом пространстве; пространстве корней; пространстве решений x(t), x’(t).(смотреть рисунок, распечатать)

1. Нелинейный осциллятор второго порядка

Систему считаем автономной и функции f-непрерывно-дифференцируемые по х

1. Способ получение характеристического уравнения.

Находим А=- Якобиан

Характеристическое уравнение имеет общий вид:

где–spurA– след (След матрицы — это сумма элементов главной диагонали матрицы)

-detA– определитель

Определить особые точки:

0=f(x) = получаем вектор Po(x|)

Характеристических уравнений столько сколько у системы особых точек.

2. Сепаратрисы и особые точки системы в фазовом пространстве.

Свойства особых точек:

1. Особые точки динамической системы x’=f(x)совпадают с точками равновесия статической системы0=f(x)

2. Статическая устойчивость точек равновесия ,

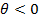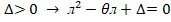
3. Уст.узел и уст. фокус – уст. равновесия статич. системы

Седло, неуст. узел, неуст. фокус – неустойчив. Равновесия статич. системы

СЕПАРАТРИСА - траектория динамической системы с двумерным фазовым пространством, стремящаяся к седловому состоянию равновесия при времени (устойчивая С.) или при (неустойчивая С.).

Сепаратрисы: ,вдоль каждой сепаратрисы можно найти точки разнообразной структуры если рассмотреть эти кривые на графике.

Важную роль имеют линии возможного разрыва: . При переходе через эти линии функцииS1,S2,S3 меняют свой знак!

3. Точечные аттракторы: устойчивый узел; устойчивый фокус.

Аттрактор (англ. attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности.

Точечный аттрактор - это простейший способ привнести порядок в хаос.

Если решение динамической системы асимптотически стремится к особой точке, то такая точка называется устойчивый узел и наоборот неустойчивй узел.

Если решение x(t) иy(t) стремятья к особой точке, при этом осциллируя, то это особоая тчка называется устойчивым фокусом. По мере увеличения времени осцилляция затухает и станоситься все менее заметной и соответсвенно тараекьория динамической системы все ближе и ближе приближается к фокусу, как бы накручивается на него.

Устойчивый центр – это когда маятник зависит от НУ, а если начальные условия (0,0), то он останентся в этом положения бесконечное время, так как НУ=(0,0).