Билет 24

Теорема. (вторая теорема Вейерштрасса) Непрерывная на сегменте функция достигает на этом сегменте своих точных граней.

Доказательство. Проведем доказательство для точной верхней грани. Допустим, что f(x), непрерывная на сегменте [a, b], не принимает ни в одной точке значения

M = f(x), тогда  x  [a, b]: f(x) < M.

Введем функцию: F(x) = > 0 и непрерывна на [a, b]. По теореме 7.2,  A > 0,  x[a,b] : F(x) =  A.  x  [a, b]: f(x)  M - < M.

Но это противоречит тому, что M – наименьшая из верхних граней функции на [a, b]. Полученное противоречие доказывает, что наше предположение неверно и, следовательно, функция достигает на сегменте [a, b] своей точной верхней грани.

Теорема доказана.

//Замечание 1. Для интервала или полусегмента теорема неверна (см. пример перед теоремой).

//Замечание 2. Если f(x) достигает на множестве X своей точной верхней грани, то она имеет на этом множестве максимальное значение, то есть f(x) = f(x), в противном случае функция не имеет на множестве X максимального значения. То же самое отн. к min и inf. Из теоремы 7.3 следует, что если f(x) непрерывна на сегменте [a, b], то она имеет на этом сегменте максимальное и минимальное значения. Ограниченная, но разрывная на сегменте функция может не иметь на этом сегменте минимального и максимального значения.

Пример. (здесь рисунок)

f(x) = . f(x) =1, минимального значения нет.

Примеры.

1. f(x) = x равномерно непрерывна на (- , ).

В самом деле,   > 0 возьмем  =  (тем самым  зависит только от  и не зависит от x).

Если x''-x' <  = , то f(x'')-f(x')= x''-x'< , а это и означает по определению, что данная функция непрерывна на всей числовой прямой.

2. f(x) = на X = {0 < x  1}.

Эта функция непрерывна на (0, 1), но не является равномерно непрерывной.

(здесь рисунок) какойто

В самом деле, возьмем  = 1 и возьмем x' = , x'' = . Тогда   > 0  N: x' - x'' < , но при этом f(x') - f(x'') = n - (n + 2) = 2 >  = 1. Тем самым, для указанного  не найдется нужного . Это и означает, что данная функция не является равномерно непрерывной на [0, 1].

и прологарифмируем его по основанию e: здесь так как функция ln(u) непрерывна в точке u=e, то переставляя местами знак предела и знак непрерывной функции получим: или

Билет 25

Следствие (прохождение непрерывной функции через любое промежуточное значение) (2 т.Коши)

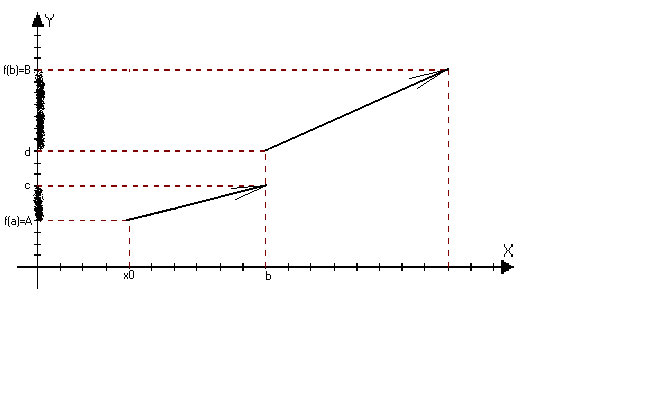
Пусть функция f(x) непрерывна на [a, b], f(а) = A, f(b) = B А≠В. Тогда  С [A, B]  c  [a, b]: f(c) = C.

Доказательство.

Рассмотрим функцию g(x) = f(x) - C. Пусть , для определённости, A < C < B. Тогда

g(a) = f(a) - С = A - C < 0, g(b) = f(b) - C = B - C > 0. Кроме того, g(x) непрерывна на сегменте

[ a, b]. Следовательно, по теореме «Если f(x) непрерывна на [a, b] и f(а) и f(b) – разных знаков, то  c  [a, b]: f(c) = 0», то c  [a, b]: g(c) = 0, то есть f(c) - C = 0  f(c) = C, что и требовалось доказать.

Следствие:

Если F(x) непрерывна на промежутке Х то ее значение сами сплошь заполняют промежуток Х=(inff(x), supf(x)).

Доказательство: Пусть м=инфинум М=супремум возьмем  у (м, М). Тогда  х1 и х2: м≤f(x1)<y<f(x2) ≤M

По 2 теореме Коши:  х:f(x)=у, то есть все значения из (м,М) явл значениями f(x).

Определение: Последовательность {x_n} называется бесконечно малой, если  ε > 0  Nε: при  n > Nε выполняется: x_n < ε.

1. бм+бм=бм

2. бм-бм=бм

3. бм*огр=бм

Все члены = одному числу С, то С=0

Б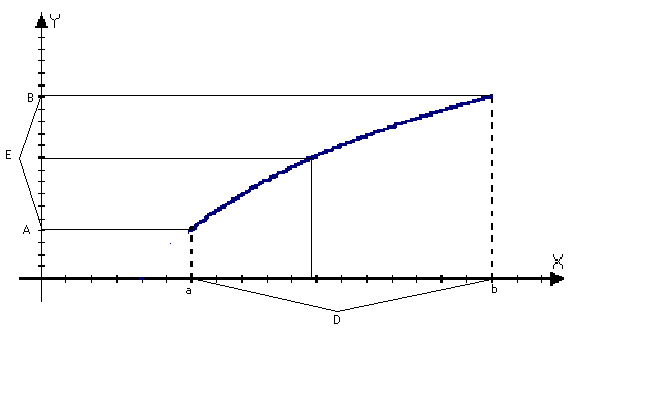 ИЛЕТ 26

Теорема: (о существование и непрерывности обратной функции) «Без доказательства»

Пусть на множестве D задана непрерывная возрастающая или убывающая функция y=f(x). Тогда на множестве её значений Е определена обратная ей функция x=g(y), которая непрерывна и возрастает или убывает на множестве Е.

Непрерывность элементарных функций.

1. y = sin x, (- < x < +).

Ранее мы доказали непрерывность функции sin x в точке x = 0.

Докажем непрерывность sin x в произвольной точке а. Для этого нужно доказать, что

sin x = sin a, или что sin x - sin a  0 при x  a. Воспользуемся формулой

sin x - sin a = 2sin cos .

Если x  a, то  0, поэтому sin  0, а так как 2cos - ограниченная функция, то sin x - sin a  0, что и требовалось доказать. Непрерывность sin x в любой точке доказана.

Рассмотрим теперь функцию у = , Х =[-  x  ]. На этом сегменте функция y = sin x является непрерывной и возрастающей (возрастание следует из формулы

sin - sin = 2sin cos ).

Следовательно, по теореме об обратной ф-ции, множеством значений данной функции является сегмент

Y = [sin(- ), sin( )] = [-1, 1], на Y= [-1, 1] существует обратная функция x = arcsin y, возрастающая и непрерывная на [-1, 1].