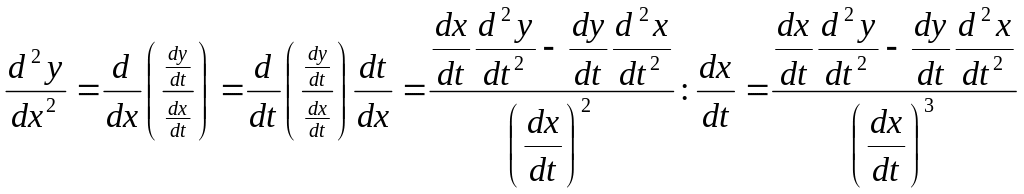Билет 30

Производная сложной функции.

Рассмотрим сложную функцию: y = f(t), где t = (x), то есть y = f((x))  F(x).

Теорема Пусть функция t = (x) дифференцируема в точке х₀, а функция y = f(t) дифференцируема в точке t₀, где t₀ = (х₀). Тогда сложная функция F(x) = f((x)) дифференцируема в точке х₀, и имеет место формула F'(х₀) = f'(t₀)'(х₀) = f'((х₀))'(х₀).

Доказательство:

Нужно доказать, что приращение функции y = F(x) = f((x)) в точке х₀ можно представить в виде: y = f'(t₀)'(х₀)x + (x)x, (1), где (x)  0 при x  0. (0) = 0. Зададим в точке х₀ приращение аргумента х, равное x. Тогда функция t = (x) получит приращение t = ( х₀ + х) - (х₀). Так как t = (x) дифференцируема в точке х₀ +, то t можно представить в виде : t = '(х₀)x + (x)x. (2), где (x)  0 при x  0. (0) = 0. Приращению t соответствует приращение y = f(t₀+t) + f'(t₀), функции y = f(t). Так как y = f(t) дифференцируема в точке t₀, то y можно представить в виде: y = f'(t₀) t + (t)t. (2), где (t)  0 при t  0. (0) = 0. (3)

Подставляя (2) в (3), получим:

y = f'( t₀ )('(х₀)x + [f'(t₀)(x) + '(х₀) + (x)]x, где [f'(t₀)(x) + '(х₀) + (x)]  (x). Очевидно, что (x)  0 при х  0, х  0.

Тем самым доказано равенство (1), и, значит, 4.4 доказана

Билет 31 Теорема

Пусть функции y=f(x) удовлетворяет всем условиям теоремы о обратной функции и имеет в точке производную , тогда обратная функция так же имеет производную в соответствующей точке и справедлива формула (6).

Дадим аргументу y обр. ф-ции в точке приращение тогда в силу строгой монотонности обр. ф-ции ее приращение в точке будет отлично от 0 и поэтому можно записать 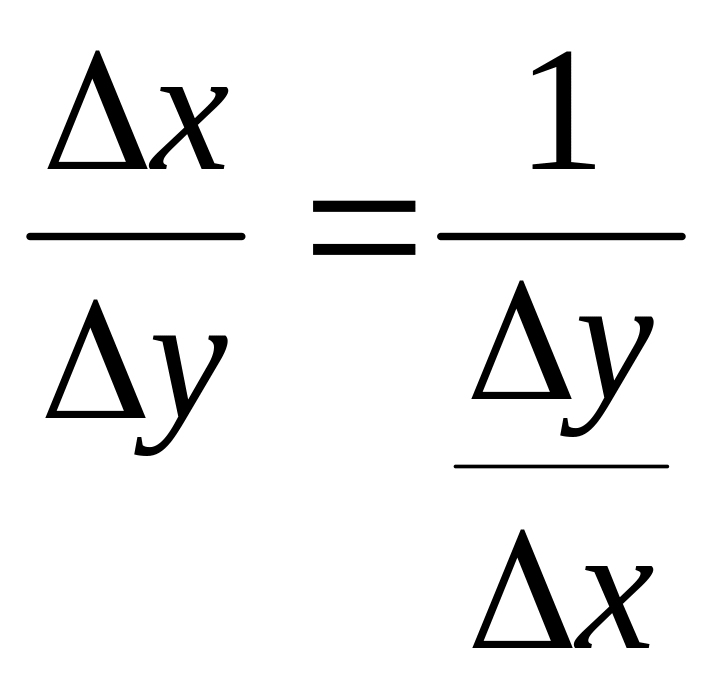. Перейдем в этом равенстве к пределу при (при этом в силу непрерывности функции y=f(x) в т. ).

Следовательно предел слева также и по определению производной есть производная .

Окончательно: .

Геометрическая иллюстрация.

имеем:

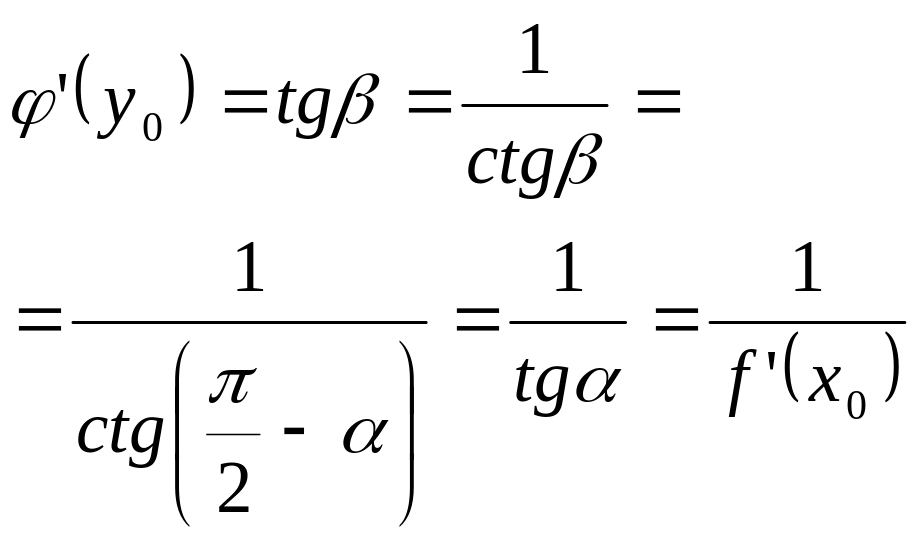
Дифференцирование функций, заданных параметрически.

Если функция y = f(x) задана в виде: , причем функция φ(t) имеет обратную функцию t = Φ(x), то у = ψ(Φ(х)), и . (18.7)

Полученная формула дает возможность находить производную функции, заданной параметрически, без определения непосредственной зависимости у от х.

Пример.

х = а(1 – cos t), y = a(t – sin t) – параметрические уравнения кривой, называемой циклоидой. Найдем у΄(х): х΄(t) = asin t, y΄(t) = a(1-cost), .

Таблица производных

y=sinx

(sinx)’=lim(^∆x0)[sin(x+∆x)-sinx]/∆x=lim(^∆x0)[2sin(∆x/2)cos((2x+∆x)/2)]/∆x=lim[2(∆x/2)cos(x+(∆x/2))]/∆x=cosx

(sinx)’=cosx

y=cos(x)

(cos(x))’=lim[cos(x+∆x)-cos(x)]/∆x=lim[-2sin(∆x/2)sin((2x+∆x)/2)]/∆x=lim[-2(∆x/2)sin(x+(∆x/2))]/∆x=-sinx

(cos(x))’=-sinx

y=tg(x)

(tg(x))’=(sin(x)/cos(x))’=[(sin(x))’cos(x)-(cos(x))’sin(x)]/cos²x=[cos²x+sin²x]/cos²x=1/cos²x

(tg(x))’=1/cos²x

y’(x)=lim[(x+∆x)ⁿ-xⁿ]/∆x=lim[xⁿ(1+(∆x/x))-1]/∆x=/∆x/x0,∆x0\=lim[xⁿ(∆x/x)n]/∆x=nx^n-1

(xⁿ)’=nx^n-1

БИЛЕТ 32

Пусть функция y=f(x) дифференцируема на некотором отрезке [ab]. В таком случае ее производная представляет собой тоже некоторую функцию х. Продифференцировав эту функцию, мы получим так называемую вторую производную (или производную второго порядка) функции f(x). Продолжая эту операцию, можно получить производные третьего, четвертого и более высоких порядков. При этом f`(x) будем называть производной первого порядка.

Определение 19.1. Производной n-го порядка (или n-й производной) от функции f(x) называется производная (первого порядка) от ее (n-1)-й производной.

Обозначение: у⁽ⁿ⁾=(y^(n-1))΄=f⁽ⁿ⁾(x). Производные 2-го и 3-го порядка обозначаются соответственно y′΄ и y΄′΄.

Примеры.

1. Найдем производную 3-го порядка от функции y=x³-5x²+3x+12.

y΄=3x²-10x+3, y΄΄=(y΄)΄=6x-10, y΄΄΄=(y΄΄)΄=6.

2. Получим общую формулу для производной n-го порядка функции y=a^bx.

y΄=a^bx·lna·b, y΄΄=lna·b(a^bx)΄=a^bx·ln²a·b²,…, y⁽ⁿ⁾=a^bx·lnⁿa·bⁿ.

Свойства производных высших порядков.

Основные свойства производных высших порядков следуют из соответствующих свойств первой производной:

1. (cf(x))⁽ⁿ⁾=c·f⁽ⁿ⁾(x).

2. (f(x)+g(x))⁽ⁿ⁾=f⁽ⁿ⁾(x)+g⁽ⁿ⁾(x).

3. Для y=x^m y⁽ⁿ⁾=n(n-1)…(n-m+1)x^m-n. Если m – натуральное число, то при n>m y⁽ⁿ⁾=0.

4. Можно вывести так называемую формулу Лейбница, позволяющую найти производную n-го порядка от произведения функций f(x)g(x):

.

Заметим, что коэффициенты в этой формуле совпадают с соответствующими коэффициентами формулы бинома Ньютона, если заменить производные данного порядка той же степенью переменной. Для n=1 эта формула была получена при изучении первой производной, для производных высших порядков ее справедливость можно доказать с помощью метода математической индукции.

5. Получим формулу для второй производной функции, заданной параметрически. Пусть x = φ(t), y = ψ(t), t₀ ≤ t ≤ T. Тогда 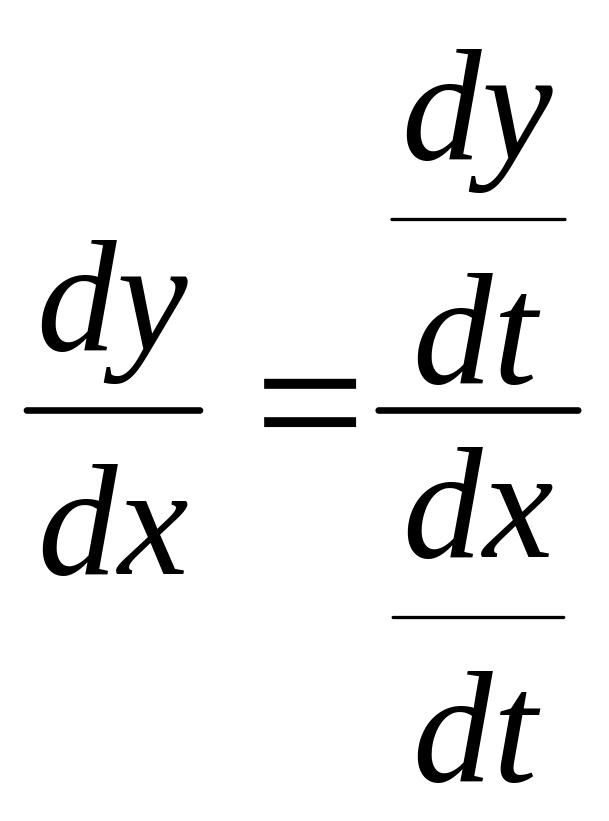. Следовательно,