2. Показниковий розподіл

Випадкову величину Х називають розподілену за показниковим законом розподілу, якщо щільність її ймовірностей має вигляд

, де >0.

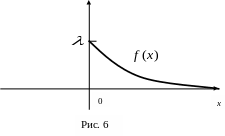
Показниковому розподілу задовольняють: час телефонної розмови, час безвідмовної роботи годинника.

Графік щільності показникового розподілу має вигляд рис. 6.

3. Нормальний розподіл

Випадкову величину Х називають розподіленою нормально, якщо щільність її ймовірностей має вигляд

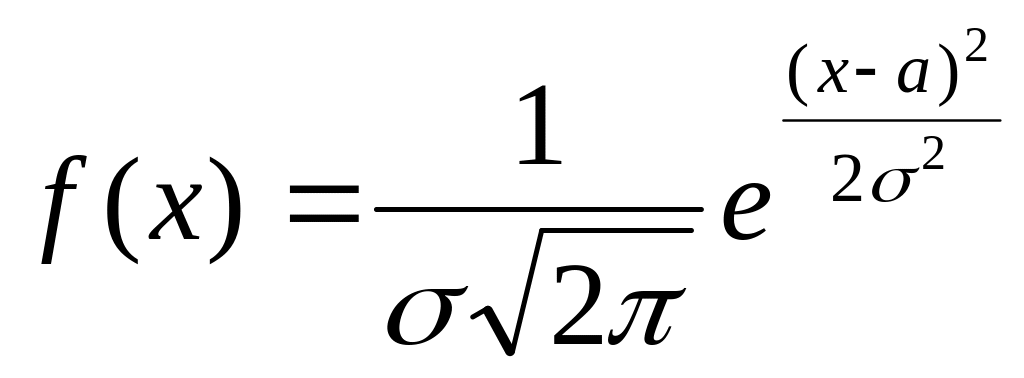, де а і – параметри розподілу.

Графік щільності нормального розподілу називають кривою Гауса і зображають рис. 7.

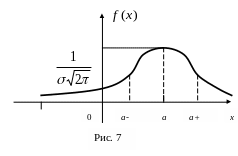
1) точки та – точки перегину.

2) max в точці , .

Для неперервних випадкових величин також можна розглядати числові характеристики. Вони обчислюються за допомогою щільності розподілу.

Числові характеристики ннв

Означення. Математичним сподіванням неперервної випадкової величини Х, заданої щільністю розподілу , називається число, яке обчислюється за формулою

Якщо неперервна випадкова величина приймає значення на відрізку [a;b] та має щільність ймовірностей , то її математичне сподівання знаходиться за формулою

Задача 5. Випадкова величина задана щільністю розподілу

Знайти математичне сподівання.

Розв’язання. .

Відповідь: .

Для неперервної випадкової величини дисперсія обчислюється за формулою:

(17)

або

(18)

Задача 6. Випадкова величина задана щільністю розподілу

Знайти дисперсію та середнє квадратичне відхилення.

Розв’язання У задачі 5 знайдено математичне сподівання .

М(Х²)= . За формулою (18) знаходимо дисперсію

.

Відповідь: , 0,2357.

Правило трьох сигм

Якщо випадкова величина Х розподілена нормально, то , тобто ймовірність того, що абсолютна величина відхилення Х від її математичного сподівання прямує до нуля, а це означає, що – практично достовірна подія.

У практиці це правило використовують так: якщо закон розподілу випадкової величини Х невідомий, але , тоді можна припустити, що Х розподілена нормально.

6.2. Закон великих чисел та центральна гранична теорема

Граничні теореми, що встановлюють граничні закони розподілу випадкових величин, об’єднують загальною назвою – центральна гранична теорема

Теорема

(Нерівність Чебишова)

Для будь-якої випадкової величини Х ймовірність того, що вона відхиляється від свого математичного сподівання більше, ніж на число , завжди менша, ніж , тобто:

(19)

У статистиці частіше використовують нерівність Чебишева для середнього квадратичного відхилення:

Граничні теореми які встановлюють відповідність між теоретичними та дослідними характеристиками випадкових подій. Об’єднують загальною назвою – закону великих чисел.

Нехай Х випадкова величина, яка має математичне сподівання М(Х) і дисперсію D(X). Нехай Х₁, Х₂, ..., Х_п випадкові величини, які мають ті ж параметри розподілу, що й Х.

Візьмемо нову випадкову величину . Застосуємо нерівність Чебишова для випадкової величини :

.

Наслідком цієї нерівності є твердження: .

Тобто середнє арифметичне результатів випробування зі зростанням п все точніше відображає математичне сподівання досліджуваної випадкової величини.