3.11. Обратная функция

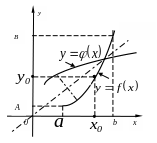
На рисунке изображен график функции , промежуток - область определения функции,

- область изменения функции. Для каждого значения аргумента из области найдётся единственное значение функции , ринадлежащее области .

Поменяем ролями переменные х и у, т.е. за аргумент (т.е. независимую переменную) возьмём у, тогда зависимой переменной (т.е. функцией) будет х.

На чертеже аргументу соответствует значение функции .

Такая зависимость называется обратной и её уравнением будет также , но функция х задана здесь в неявной форме. Если из этого равенства выразить х, то получим обратную зависимость в явной форме: . Областью определения этой функции будет промежуток , а областью изменения функции будет .

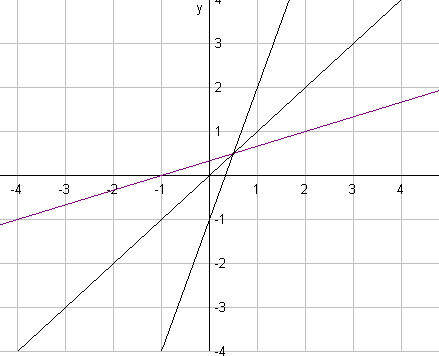
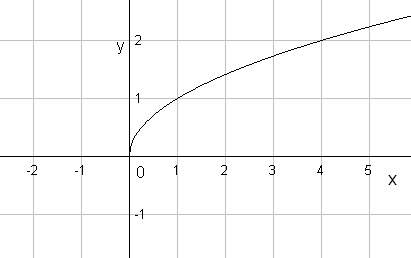
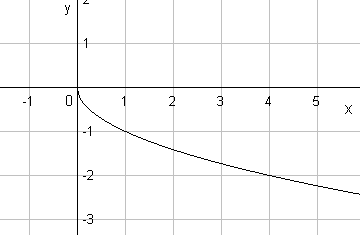
Графиком функции будет та же самая кривая, но смотреть на него надо по особенному: осью аргумента является вертикальная ось, а осью значений функции – горизонтальная. Чтобы исключить это неудобство, т.е. как обычно ось аргумента расположить горизонтально (слева направо), а ось значений функции вертикально (снизу вверх), надо поменять ролями буквы х и у, т.е. записать обратную зависимость в виде .Функции и различаются только обозначениями переменных. Поэтому, чтобы из графика (или, что то же, функции ) получить график функции , достаточно поменять ролями оси Ох и Оу, т.е. повернуть плоскость чертежа вокруг биссектрисы первого координатного угла на 180° ; другими словами, . для получения графика обратной функции в привычной системе координат надо график прямой функции отразить симметрично относительно прямой у = х.

Пример. Для функции найти обратную. Построить графики прямой и обратной функций.

Решение.

Из уравнения выражаем х : .
Меняем ролями х и у : . Это и будет обратная функция.

Проблема существования обратной функции

Всегда ли для функции существует обратная? Не всегда! На этот счёт существует теорема:

Если функция в некоторой области монотонна (или возрастает или убывает), то для неё в этой области существует обратная.

Пример.

На рисунке изображен график функции . На интервале эта функция не является монотонной. Следовательно, для неё не существует обратной функции: для одного значения у существует два ( а не одно !) значение х.

Если же функцию рассмотреть на промежутке , то функция будет монотонной и для неё существует обратная: . На промежутке функция также монотонная, для неё существует обратная : (см. рис.).