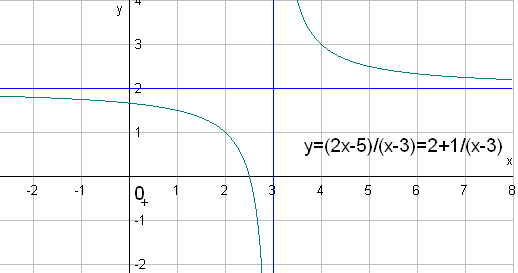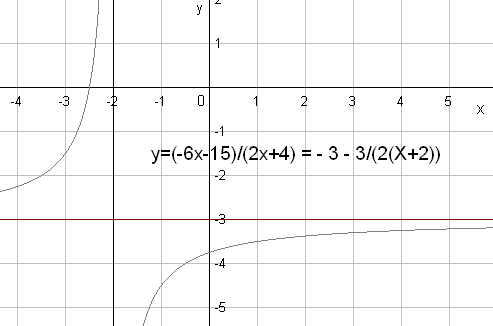- •Математические обозначения. Таблицы
- •Латинский алфавит
- •1.2. Греческий алфавит
- •1. 3. Математические обозначения
- •Некоторые исторические факты математических символов
- •Важнейшие постоянные
- •1.8. Некоторые степени чисел 2, 3, 5
- •1.9. Факториалы
- •Перевод градусной меры в радианную
- •Арифметика
- •Признаки делимости
- •2.2. Средние величины
- •Действительные числа
- •Действия над дробями
- •Пропорции
- •3.4. Абсолютная величина действительного числа (модуль)
- •Формулы сокращенного умножения
- •Квадратные уравнения
- •Разложение на множители
- •Аргумент, функция
- •Элементы поведения функции
- •Возрастающие и убывающие функции (монотонные функции)
- •Четные и нечётные функции
- •Периодические функции
- •Корни функции
- •Чтение графиков функций
- •3.11. Обратная функция
- •Проблема существования обратной функции
- •3.13. Основные элементарные функции
- •3.14. Степени и корни
- •3.16. Целая рациональная функция (или многочлен)
- •3.17. Квадратичная функция
- •3.18. Рациональная функция
- •3.19. Дробно-линейная функция
- •3.20. Показательная функция
- •3.21. Логарифмы. Логарифмическая функция
- •3.22. Гиперболические функции
- •Определения
- •Основные соотношения
- •3.22.3. Графики гиперболических функций
- •3.24. Соединения (размещения, перестановки, сочетания)
- •Бином ньютона
- •3.26. Комплексные числа
- •3.26.1. Комплексные числа в алгебраической форме
- •3.26.2. Тригонометрическая форма комплексного числа
- •Действия над комплексными числами в тригонометрической форме
- •3.26.3. Показательная форма комплексного числа
- •3.27. Элементарные приёмы построения
- •3.27.1. Преобразования графиков
- •3.27.2. Сложение графиков
- •3.28. Графики некоторых функций, содержащие
- •3.29. Прогрессии
- •Арифметическая прогрессия
3.16. Целая рациональная функция (или многочлен)
![]() ,
,
![]()
- многочлен степени
n;
![]() -
коэффициенты многочлена,
-
коэффициенты многочлена,
![]() -
коэффициент при старшем
члене,
-
коэффициент при старшем
члене,
![]() -
свободный член многочлена.
-
свободный член многочлена.
3.17. Квадратичная функция
Примером целой
рациональной функции является квадратичная
функция
![]() ;
здесь
-
коэффициенты, причём
;
здесь
-
коэффициенты, причём
![]() ,
,
![]() -
любые числа.
-
любые числа.
Графиком функции является парабола.
Частные случаи:
![]()
a>0
a<0 |
Примеры: (1): (3): (5): (8): |
Общий случай:
![]() .
Выражение
.
Выражение
![]() - дискриминант,
- дискриминант,
![]() -
корни квадратного трехчлена,
-
корни квадратного трехчлена,
![]() - абсцисса вершины параболы.
- абсцисса вершины параболы.
x1 х0 x2
Дискриминант
D
> 0
– два различных корня (парабола
пересекает ось Ох в двух точках):
|
X1 ,2
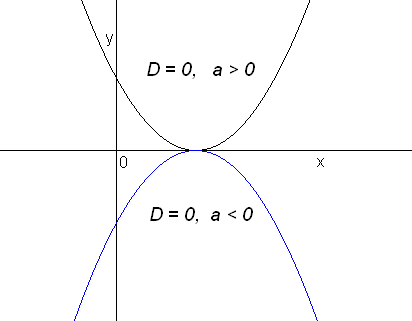
Дискриминант D = 0 – корни равные (парабола касается оси Ох) :
|
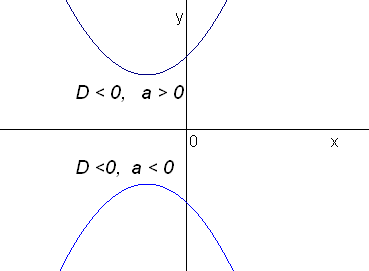
Дискриминант
D
< 0
– действительных корней нет (парабола
не пересекает и не касается оси Ох)
|
3.18. Рациональная функция
Отношение двух многочленов называется рациональной функцией
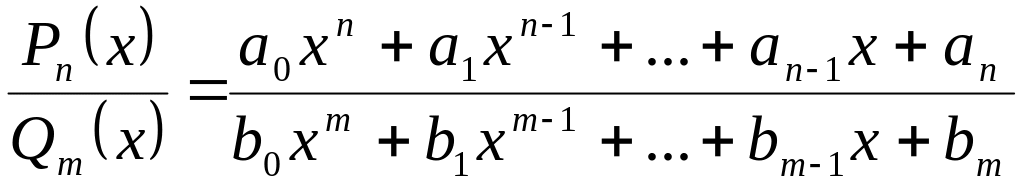 .
.
Если
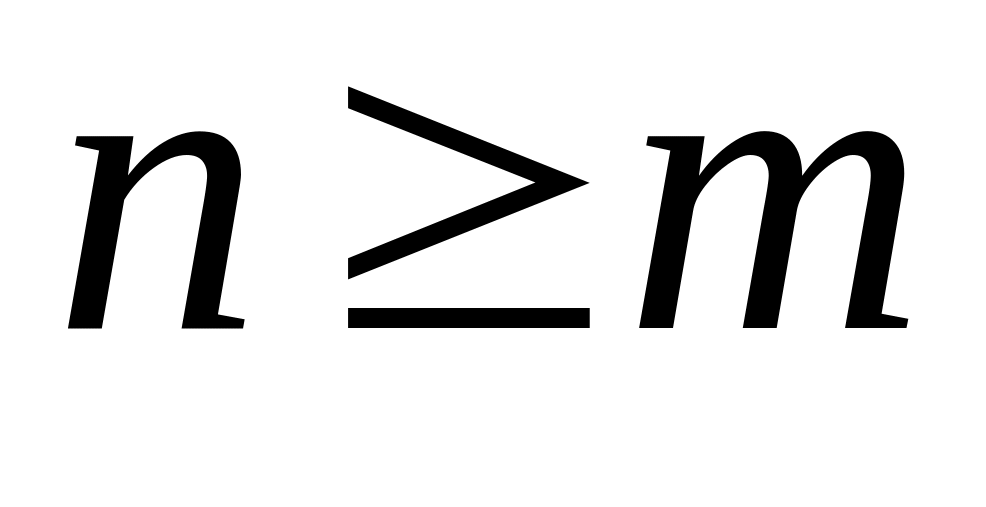 ,
то рациональная функция (рациональная
дробь) называется неправильной,
если
,
то рациональная функция (рациональная
дробь) называется неправильной,
если
 ,
то правильной.
,
то правильной.Если дробь
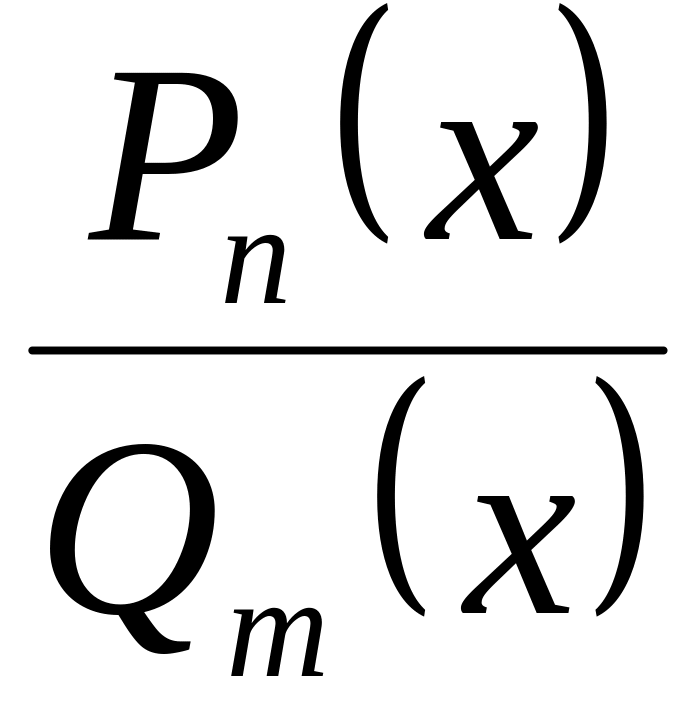 - неправильная,
её всегда можно представить в виде
- неправильная,
её всегда можно представить в виде
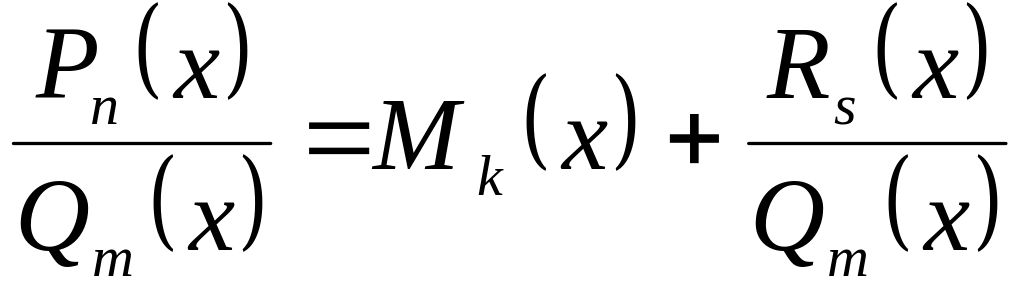 ,
где дробь
,
где дробь
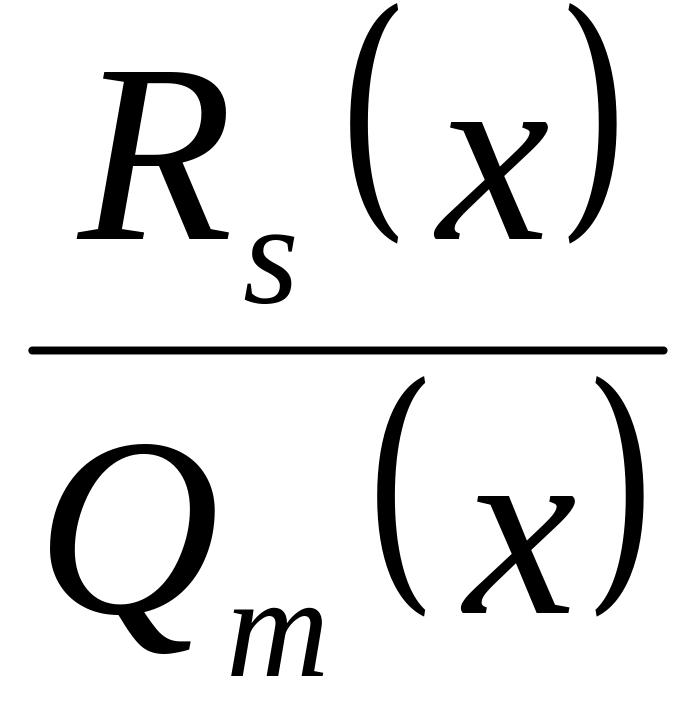 - правильная
(
- правильная
(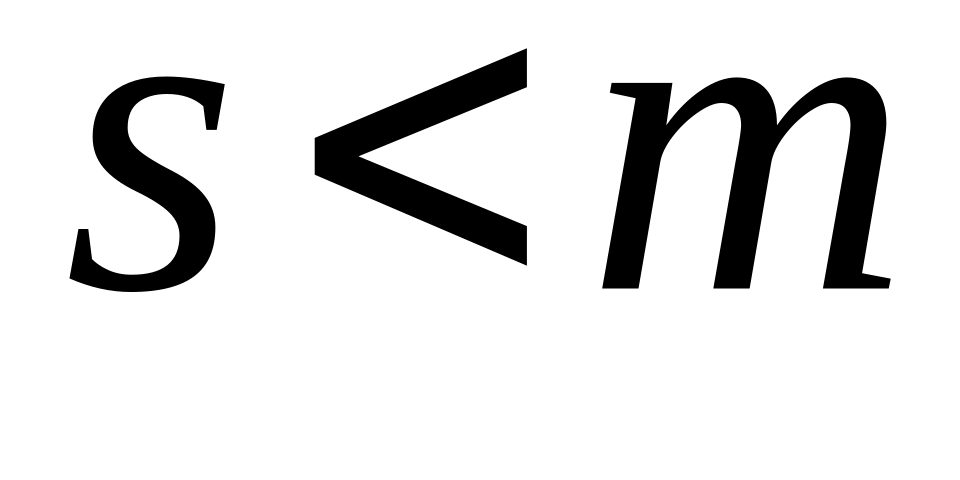 ).
Этого можно достигнуть с помощью деления
“ уголком”.
).
Этого можно достигнуть с помощью деления
“ уголком”.
Пример.
|
3.19. Дробно-линейная функция
Простейшим случаем
рациональной функции является
дробно-линейная функция
![]() ,
где
коэффициенты
,
где
коэффициенты
![]() -
любые числа
и определитель
-
любые числа
и определитель
![]() .
Это условие означает, что
.
Это условие означает, что
![]() Графиком этой функции является гипербола
со смещённым центром и асимптотами,
параллельными осям координат.
Графиком этой функции является гипербола
со смещённым центром и асимптотами,
параллельными осям координат.
Примеры.
|
|
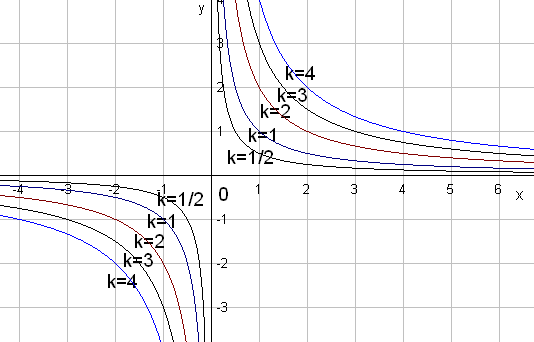
Частным случаем
дробно-линейной функции является функция
![]() .
Её графиком является гипербола с центром
в начале координат (асимптотами являются
оси координат). По-другому функцию
называют законом обратной пропорциональности,
k
– коэффициент пропорциональности.
.
Её графиком является гипербола с центром
в начале координат (асимптотами являются
оси координат). По-другому функцию
называют законом обратной пропорциональности,
k
– коэффициент пропорциональности.
|
|
3.20. Показательная функция
(0<a<1) ( a>1)
|
|
3.21. Логарифмы. Логарифмическая функция
1). Если
![]() то
то
![]() ,
( а
> 0,
а
1,
b>0
).
,
( а
> 0,
а
1,
b>0
).
Логарифмы, взятые по основанию 10, называются десятичными, а по основанию е = 2,718281828459...- натуральными и обозначаются, соответственно, lg , ln .
Из определения логарифмов имеем
![]() -
основное логарифмическое тождество.
-
основное логарифмическое тождество.
2). Свойства логарифмов
8.
|
11.
12.
13. При a > 1
При 0 < a < 1 наоборот,
|
Определение.
Функция,
обратная показательной функции
![]() ,
где
,
где
![]() ,
называется логарифмической функцией
и обозначается
,
называется логарифмической функцией
и обозначается
![]()
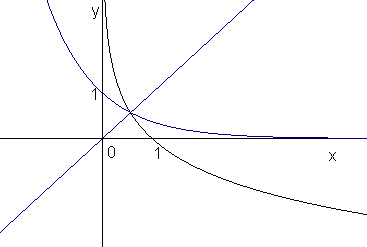
График логарифмической функции. Он симметричен графику
показательной функции относительно биссектрисы 1-го и 3-го координатных углов
|
|
4) Графики логарифмической функции при различных основаниях a

![]()
![]()
![]()
![]()
![]()
![]()