
- •1. Закон Кулона. Закон сохранения заряда. Принцип суперпозиции.
- •2. Электростатическое поле (напряженность электростатического поля, поле точечного покоящегося электрического заряда, потенциальность поля)
- •3. Основная задача электростатики (для точечных зарядов в вакууме, для произвольного объемного, поверхностного и линейного распределения зарядов)
- •4. Дифференциальные операторы (оператора (набла), дивергенция функции divF, ротор функции rotF)
- •5. Безвихревой характер электростатического поля
- •6. Поток вектора напряженности
- •7. Теорема Гаусса (в том числе - для точечного заряда)
- •8. Применение теоремы Гаусса для расчета полей - поле бесконечной, прямой, равномерно заряженной нити
- •9. Применение теоремы Гаусса для расчета полей - поле бесконечной, равномерно заряженной плоскости
- •10. Применение теоремы Гаусса для расчета полей - поле сферической, равномерно заряженной поверхности
- •11. Теорема Гаусса в дифференциальной форме (вакуум).
- •12. Уравнение Пуассона (вакуум).
- •13. Плотность заряда для точечного заряда (δ-функция).
- •14. Поле Диполя.
- •15. Диэлектрики и вектор поляризации.
- •16. Основная задача электростатики для поля в диэлектрике (истинные и связанные заряды).
- •17. Уравнение Пуассона для поля в диэлектрике.
- •19. Теорема Гаусса для поля в диэлектрике (интегральная форма).
- •20. Закон Кулона в диэлектрике (Теорема Гаусса для поля в диэлектрике).
- •21. Свойства проводников
- •22. Метод изображений (для бесконечно проводящей плоскости и сферы)
- •23. Электроемкость уединенного проводника
- •24. Конденсатор – Сферический конденсатор
- •25. Конденсатор – Плоский конденсатор
- •26. Конденсатор – Соединения конденсаторов
- •27. Энергия заряженного проводника
- •28. Энергия электростатического поля
- •29. Ток и плотность тока
- •1. Работа тока (вдоль произвольного контура, мощность и удельная мощность тока)
- •2. Интегральные закона Ома (для участка цепи, содержащего эдс - определение эдс и сопротивления участка цепи; для замкнутого проводника; для участка цепи не содержащего эдс)
- •3. Закон Ома в дифференциальной форме.
- •4. Тепловое действие тока (закон Джоуля-Ленца в дифференциальной и интегральной формах)
- •5. Правила Кирхгофа.
- •6 . Постулат Ампера
- •7. Закон Био-Савара-Лапласса
- •8. Силовое действие магнитного поля – закон Ампера
- •9. Закон Ампера: сила Лоренца, сила Ампера
- •10. Силовое действие магнитного поля – принцип действия электромотора
- •11. Силовое действие магнитного поля – принцип действия электромотора.
- •12. Калибровочная инвариантность магнитного поля
- •13. Применение закона бсл для расчета магнитных полей – поле бесконечного, прямого проводника с постоянным током.
- •14. Применение закона бсл для расчета магнитных полей – поле кругового проводника с постоянным током.
- •15. Закон полного тока – уравнение Пуассона для магнитного поля.
- •16. Закон полного тока (в дифференциальной и интегральной формах)
- •17. Применение закона полного тока для расчета магнитных полей – поле бесконечного, прямого проводника с постоянным током.
- •18. Применение закона полного тока для расчета магнитных полей – поле бесконечного соленоида с постоянным током.
- •19. Теорема Гаусса для магнитного поля.
- •20. Магнитный момент.
- •21. Магнитная восприимчивость
- •22. Закон полного тока для магнитного поля в магнетике
- •23. Уравнение Пуассона для магнитного поля в магнетике
- •24. Векторный потенциал магнитного поля в магнитной среде
- •25. Типы магнетизма (Суперпарамагнетизм, Антиферромагнетизм (Клапаны вращения), Ферримагнетизм, Ферромагнетизм (Ферромагнитные материалы), Парамагнетизм, Диамагнетизм)
- •26. Магнетизм вещества.
1. Работа тока (вдоль произвольного контура, мощность и удельная мощность тока)
По
определению (![]() ),
плотность тока обеспечивает перенос
зарядов из одной точки пространства в
другую – т.е. совершает работу.
Соответственно, на элементарном
перемещении dr плотность тока j совершает
элементарную работу
),
плотность тока обеспечивает перенос
зарядов из одной точки пространства в
другую – т.е. совершает работу.
Соответственно, на элементарном
перемещении dr плотность тока j совершает
элементарную работу
![]() ,
где
,
где
![]() - удельное сопротивление вещества (в
котором течёт ток.)
- удельное сопротивление вещества (в
котором течёт ток.)
Таким
образом, работа тока вдоль произвольного
контура L:
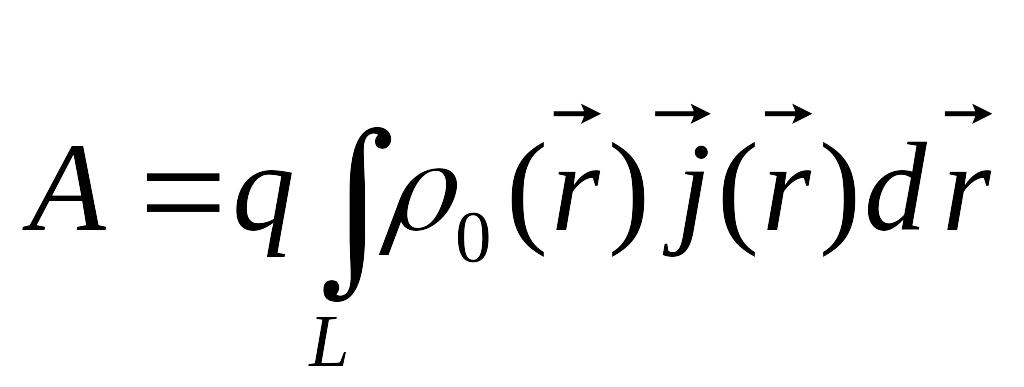 .
Заметим, что работа зависит от формы
контура L.
.
Заметим, что работа зависит от формы
контура L.
Работу
в единицу времени называют мощностью
– следовательно мощность тока
 =>
=>

Мощность
тока N – характеристика данной точки
пространства (с радиус-вектором r, т.е.
дифференциальная характеристика) –
мощность, приходя-щуюся на элементарный
объём dV, называеют удельной мощностью
![]() .
.
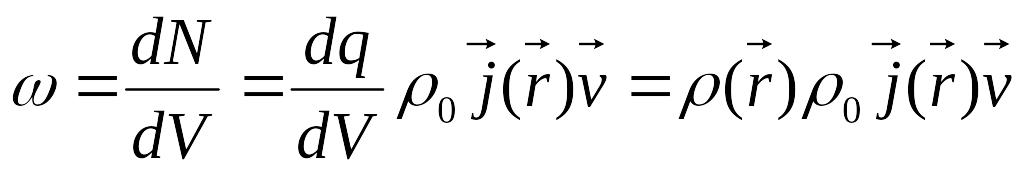 =>
=>
![]()
2. Интегральные закона Ома (для участка цепи, содержащего эдс - определение эдс и сопротивления участка цепи; для замкнутого проводника; для участка цепи не содержащего эдс)
Рассмотрим движение зарядов внутри проводника. Согласно , элементарная работа плотности тока по перемещению заряда
Эту
же работу можно рассматривать как работу
электрического поля
![]() .
Как и любое силовое поле, электрическое
поле можно разделить на две составляющие
– потенциальное (т.е. электростатическое)
и непотенциальное:
.
Как и любое силовое поле, электрическое
поле можно разделить на две составляющие
– потенциальное (т.е. электростатическое)
и непотенциальное:
![]() .
.
Тогда, интегрируя выражения для работы, можно получить :
В
силу равенства элементарных работ
плотности тока и электрического поля
![]() . Проинтегрируем это равенство по всему
объёму V проводника (очевидно, V=SL):
. Проинтегрируем это равенство по всему
объёму V проводника (очевидно, V=SL):
 (*1)
(*1)
Вычислим
сначала интеграл от поля:
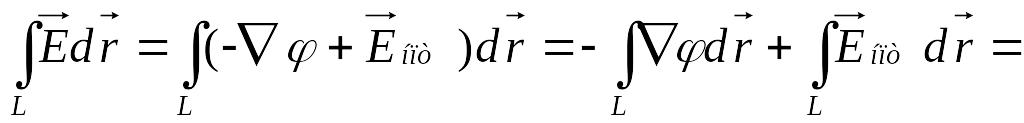
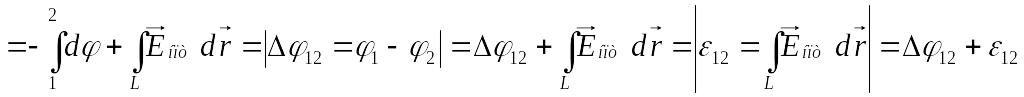
Здесь
![]() - разность потенциалов на участке цепи,
соответственно,
- разность потенциалов на участке цепи,
соответственно,
![]() - называют электродвижущей силой (ЭДС)
на участке цепи.
- называют электродвижущей силой (ЭДС)
на участке цепи.
Из
опытных фактов очевидно, что эти величины
не зависят от конфигурации сечение
проводника в любой его точке, т.е.
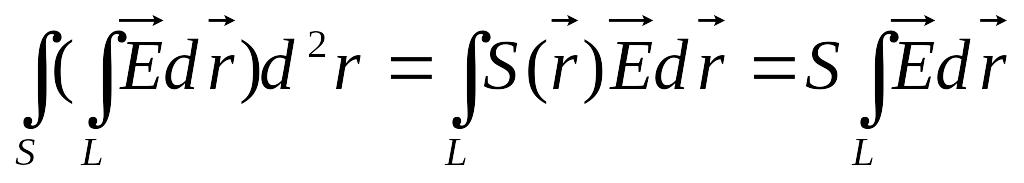 .
.
Займёмся
теперь интегралом от плотности тока:
 =
=
= .
.
Таким
образом уравнение (*1) принимает вид:
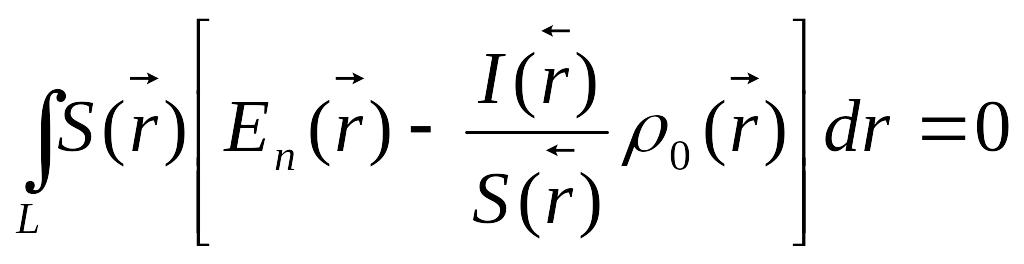 ,
здесь
,
здесь
![]() - проекция вектора Е на dr
- проекция вектора Е на dr
Отношение
 - есть среднее значение плотности тока
в сечении проводника с радиус-вектором
r.
- есть среднее значение плотности тока
в сечении проводника с радиус-вектором
r.
Это
означает, что выражение в квадратных
скобках не зависит от конфигурации
сечения проводника в любой его точке,
т.е.
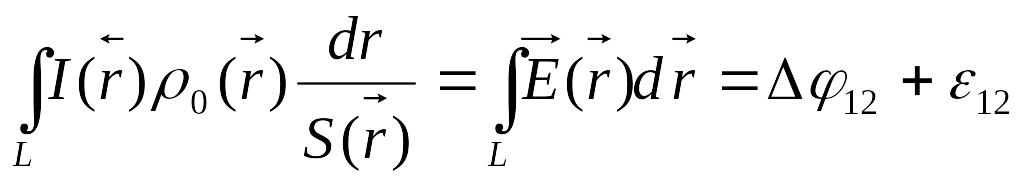 .
.
Если
проводник достаточно гладкий и однородный,
так, что сила тока в проводнике в любой
его точке постоянна, то
 .
.
![]() -
это Интегральный закон Ома для участка
цепи, содержащего ЭДС. Величину
-
это Интегральный закон Ома для участка
цепи, содержащего ЭДС. Величину
![]() - называют напряжением на участке цепи,
соответственно, произведение
- называют напряжением на участке цепи,
соответственно, произведение
![]() - называют падением напряжения на
сопротивление
- называют падением напряжения на
сопротивление
![]() .
Здесь,
.
Здесь,
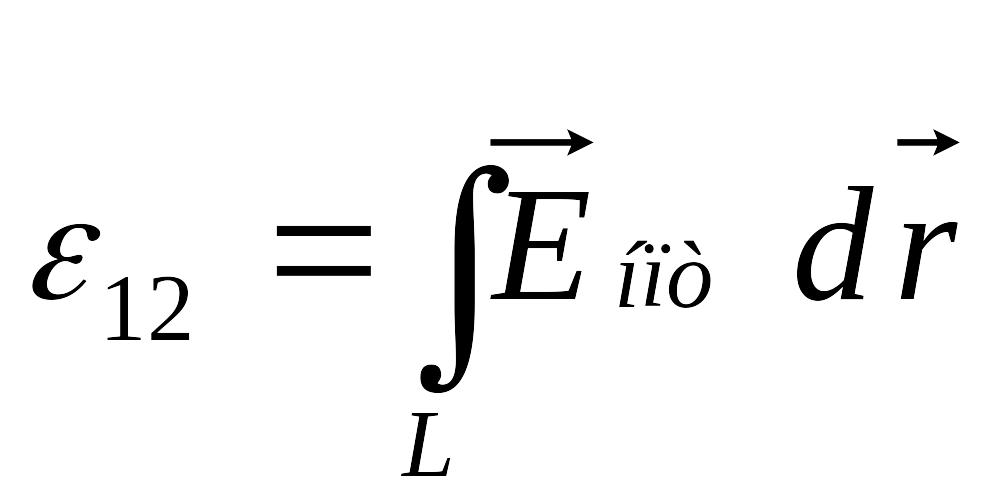 - ЭДС,
- ЭДС,
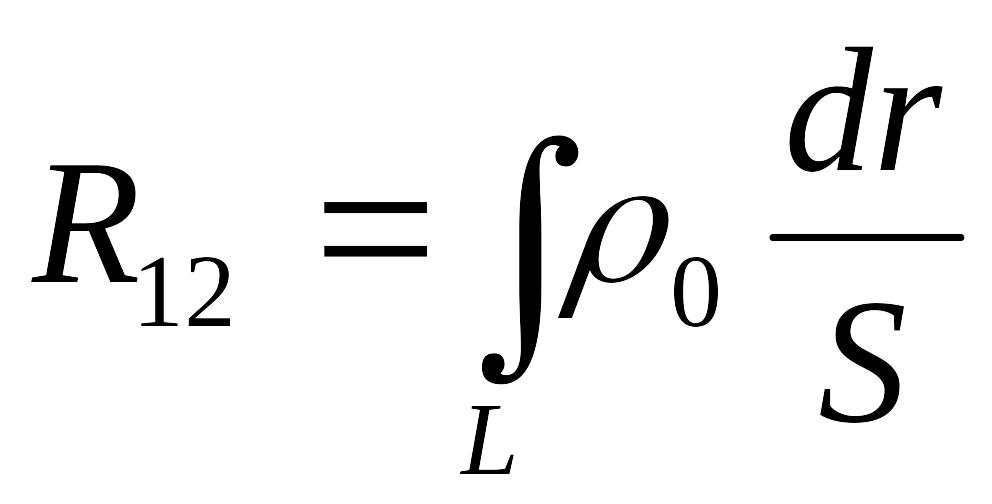 - сопротивление.
- сопротивление.
Ч астные
случаи:
астные
случаи:
Для
замкнутого проводника, очевидно
![]() ,
и мы получаем интегральный закон Ома
для замкнутой цепи:
,
и мы получаем интегральный закон Ома
для замкнутой цепи:
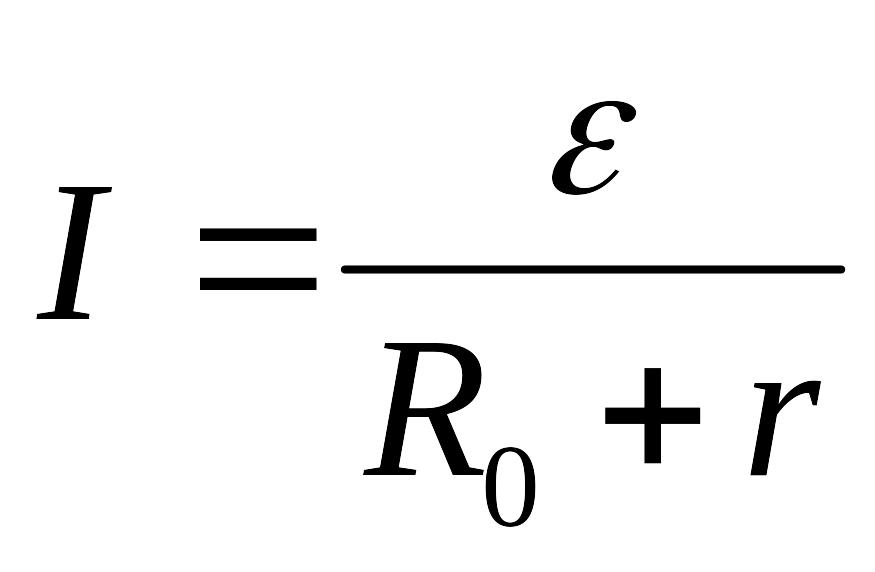 .
Здесь
.
Здесь
![]() ,
причём
,
причём
![]() - сопротивление внешней цепи, r –
(внутреннее) сопротивление ЭДС,
- сопротивление внешней цепи, r –
(внутреннее) сопротивление ЭДС,
![]() - алгебраическая сумма всех ЭДС в цепи.
- алгебраическая сумма всех ЭДС в цепи.
Если
![]() ,
то получаем интегральный закон Ома для
участка цепи, не содержащего ЭДС.
,
то получаем интегральный закон Ома для
участка цепи, не содержащего ЭДС.
![]()
![]() .
.
Отметим, что напряжение на участке цепи , в общем случае, НЕ равно падению напряжения IR на сопротивлении R.
3. Закон Ома в дифференциальной форме.
Как мы уже выяснили, элементарная работа по перемещению зарядов внутри проводника может быть выражена через плотность тока: .
Эту же работу можно рассматривать как работу электрического поля . В силу равенства элементарных работ плотности тока и электрического поля .
Откуда
получаем:
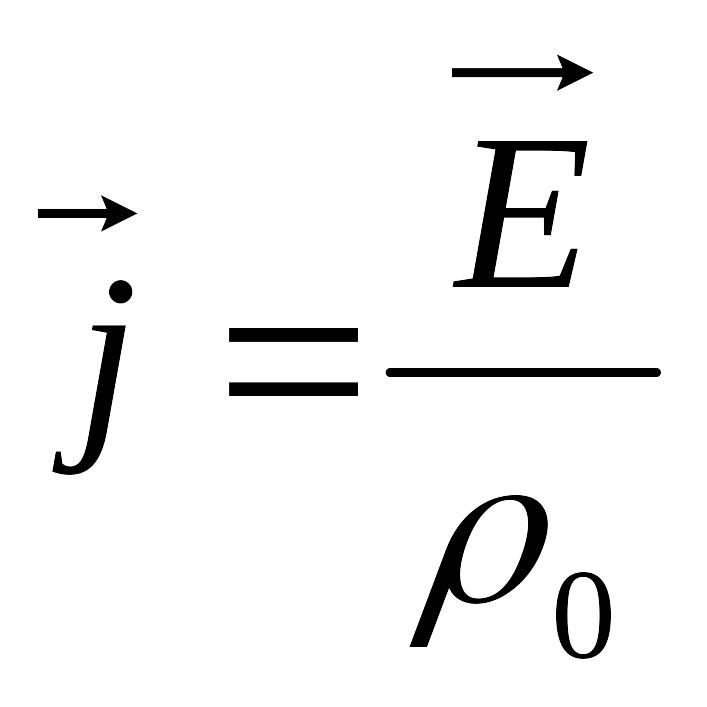 => закон Ома в дифференциальной форме
=>
=> закон Ома в дифференциальной форме
=>![]() .
.
Плотность тока в любой точке проводника пропорциональна напряжённости электрического поля в этой точке.
Величину
![]() называют
удельной проводимостью.
называют
удельной проводимостью.
