
- •1. Закон Кулона. Закон сохранения заряда. Принцип суперпозиции.
- •2. Электростатическое поле (напряженность электростатического поля, поле точечного покоящегося электрического заряда, потенциальность поля)
- •3. Основная задача электростатики (для точечных зарядов в вакууме, для произвольного объемного, поверхностного и линейного распределения зарядов)
- •4. Дифференциальные операторы (оператора (набла), дивергенция функции divF, ротор функции rotF)
- •5. Безвихревой характер электростатического поля
- •6. Поток вектора напряженности
- •7. Теорема Гаусса (в том числе - для точечного заряда)
- •8. Применение теоремы Гаусса для расчета полей - поле бесконечной, прямой, равномерно заряженной нити
- •9. Применение теоремы Гаусса для расчета полей - поле бесконечной, равномерно заряженной плоскости
- •10. Применение теоремы Гаусса для расчета полей - поле сферической, равномерно заряженной поверхности
- •11. Теорема Гаусса в дифференциальной форме (вакуум).
- •12. Уравнение Пуассона (вакуум).
- •13. Плотность заряда для точечного заряда (δ-функция).
- •14. Поле Диполя.
- •15. Диэлектрики и вектор поляризации.
- •16. Основная задача электростатики для поля в диэлектрике (истинные и связанные заряды).
- •17. Уравнение Пуассона для поля в диэлектрике.
- •19. Теорема Гаусса для поля в диэлектрике (интегральная форма).
- •20. Закон Кулона в диэлектрике (Теорема Гаусса для поля в диэлектрике).
- •21. Свойства проводников
- •22. Метод изображений (для бесконечно проводящей плоскости и сферы)
- •23. Электроемкость уединенного проводника
- •24. Конденсатор – Сферический конденсатор
- •25. Конденсатор – Плоский конденсатор
- •26. Конденсатор – Соединения конденсаторов
- •27. Энергия заряженного проводника
- •28. Энергия электростатического поля
- •29. Ток и плотность тока
- •1. Работа тока (вдоль произвольного контура, мощность и удельная мощность тока)
- •2. Интегральные закона Ома (для участка цепи, содержащего эдс - определение эдс и сопротивления участка цепи; для замкнутого проводника; для участка цепи не содержащего эдс)
- •3. Закон Ома в дифференциальной форме.
- •4. Тепловое действие тока (закон Джоуля-Ленца в дифференциальной и интегральной формах)
- •5. Правила Кирхгофа.
- •6 . Постулат Ампера
- •7. Закон Био-Савара-Лапласса
- •8. Силовое действие магнитного поля – закон Ампера
- •9. Закон Ампера: сила Лоренца, сила Ампера
- •10. Силовое действие магнитного поля – принцип действия электромотора
- •11. Силовое действие магнитного поля – принцип действия электромотора.
- •12. Калибровочная инвариантность магнитного поля
- •13. Применение закона бсл для расчета магнитных полей – поле бесконечного, прямого проводника с постоянным током.
- •14. Применение закона бсл для расчета магнитных полей – поле кругового проводника с постоянным током.
- •15. Закон полного тока – уравнение Пуассона для магнитного поля.
- •16. Закон полного тока (в дифференциальной и интегральной формах)
- •17. Применение закона полного тока для расчета магнитных полей – поле бесконечного, прямого проводника с постоянным током.
- •18. Применение закона полного тока для расчета магнитных полей – поле бесконечного соленоида с постоянным током.
- •19. Теорема Гаусса для магнитного поля.
- •20. Магнитный момент.
- •21. Магнитная восприимчивость
- •22. Закон полного тока для магнитного поля в магнетике
- •23. Уравнение Пуассона для магнитного поля в магнетике
- •24. Векторный потенциал магнитного поля в магнитной среде
- •25. Типы магнетизма (Суперпарамагнетизм, Антиферромагнетизм (Клапаны вращения), Ферримагнетизм, Ферромагнетизм (Ферромагнитные материалы), Парамагнетизм, Диамагнетизм)
- •26. Магнетизм вещества.
8. Применение теоремы Гаусса для расчета полей - поле бесконечной, прямой, равномерно заряженной нити
Для расчёта электростатического поля зарядов, с заданным распределением, по теореме Гаусса нужно:
1. Выбрать замкнутую поверхность, охватывающую эту систему зарядов, следующим образом:
- поверхность не соприкасается с заряженным телом
- поверхность является эквипотенциальной
- поверхность является образующей какой-либо(из известных) систем координат
2. Записать теорему Гаусса для выбранной поверхности и
- вычислить поток, учитывая эквипотенциальность выбранной поверхности
- вычислить заряд, учитывая симметрию
распределения заряда
вычислить заряд, учитывая симметрию
распределения заряда
![]()
![]()
![]()
Поле бесконечной, прямой, равномерно заряженной нити
Линейную
плотность заряда на нити
![]() будем
считать постоянной. Из физических
соображений ясно, что эквипотенциальной
поверхностью для нити является
коаксиальная цилиндрическая поверхность
– с торцевыми «заглушками» на
бесконечности. Для любой точки боковой
поверхности цилиндра вектор напряженности
E
параллелен вектору нормали к боковой
поверхности dSб
будем
считать постоянной. Из физических
соображений ясно, что эквипотенциальной
поверхностью для нити является
коаксиальная цилиндрическая поверхность
– с торцевыми «заглушками» на
бесконечности. Для любой точки боковой
поверхности цилиндра вектор напряженности
E
параллелен вектору нормали к боковой
поверхности dSб
Таким
образом теорема Гаусса для нити принимает
вид
![]()
И
после несложных преобразований получаем
![]() ,
где «a»
расстояние от нити(радиус цилиндра).
,
где «a»
расстояние от нити(радиус цилиндра).

9. Применение теоремы Гаусса для расчета полей - поле бесконечной, равномерно заряженной плоскости
Для расчёта электростатического поля зарядов, с заданным распределением, по теореме Гаусса нужно:
1. Выбрать замкнутую поверхность, охватывающую эту систему зарядов, следующим образом:
- поверхность не соприкасается с заряженным телом
- поверхность является эквипотенциальной
- поверхность является образующей какой-либо(из известных) систем координат
2. Записать теорему Гаусса для выбранной поверхности и
- вычислить поток, учитывая эквипотенциальность выбранной поверхности
- вычислить заряд, учитывая симметрию распределения заряда
Поле бесконечной, равномерно заряженной плоскости
Поверхностную
плотность заряда на плоскости
![]() будем считать постоянной. Из физических
соображений ясно, что эквипотенциальной
поверхностью для плоскости является
поверхность параллелепипеда – с боковыми
поверхностями на бесконечности. Любую
бесконечную плоскость можно представить
как множество бесконечных прямых –
потому для любой точки поверхностей
параллелепипеда, параллельных заряженной
плоскости, вектор напряженности E
параллелен вектору нормали к поверхности
dSII.
будем считать постоянной. Из физических
соображений ясно, что эквипотенциальной
поверхностью для плоскости является
поверхность параллелепипеда – с боковыми
поверхностями на бесконечности. Любую
бесконечную плоскость можно представить
как множество бесконечных прямых –
потому для любой точки поверхностей
параллелепипеда, параллельных заряженной
плоскости, вектор напряженности E
параллелен вектору нормали к поверхности
dSII.
Т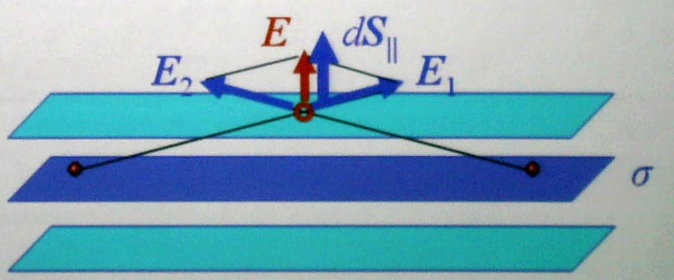 аким
образом теорема Гаусса для плоскости
принимает вид
аким
образом теорема Гаусса для плоскости
принимает вид
![]() и
после несложных преобразований получаем
и
после несложных преобразований получаем
![]()
«Напряженность поля над и под плоскостью одинакова по величине и не зависит от расстояния от плоскости.»
10. Применение теоремы Гаусса для расчета полей - поле сферической, равномерно заряженной поверхности
Для расчёта электростатического поля зарядов, с заданным распределением, по теореме Гаусса нужно:
1. Выбрать замкнутую поверхность, охватывающую эту систему зарядов, следующим образом:
- поверхность не соприкасается с заряженным телом
- поверхность является эквипотенциальной
- поверхность является образующей какой-либо(из известных) систем координат
2. Записать теорему Гаусса для выбранной поверхности и
- вычислить поток, учитывая эквипотенциальность выбранной поверхности
- вычислить заряд, учитывая симметрию распределения заряда
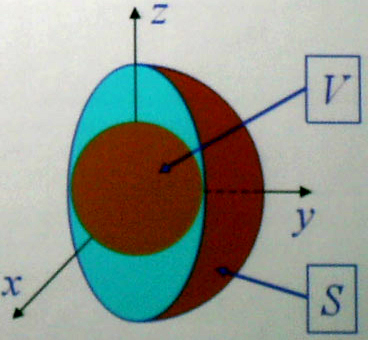
Поле сферической, равномерно заряженной поверхности
П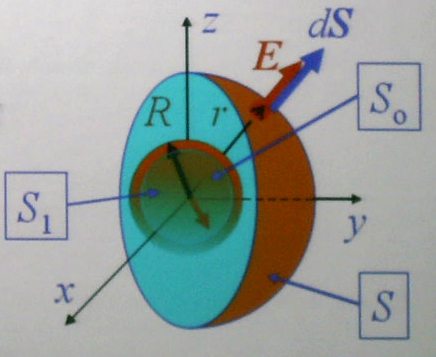 оверхностную
плотность заряда на сфере S0
будем считать постоянной.
Очевидно, что эквипотенциальной
поверхностью
для сферической поверхности является
сфера. Для любой точки поверхности сферы
S(охватывающей
заряженную сферу S0
и проходящей
через точку с радиус-вектором r,
в которой вычисляется поле), вектор
напряжённости E
параллелен
вектору нормали
к поверхности dS.
Таким образом теорема Гаусса для
сферической, равномерно заряженной
поверхности принимает вид
После
несложных преобразований получаем
оверхностную
плотность заряда на сфере S0
будем считать постоянной.
Очевидно, что эквипотенциальной
поверхностью
для сферической поверхности является
сфера. Для любой точки поверхности сферы
S(охватывающей
заряженную сферу S0
и проходящей
через точку с радиус-вектором r,
в которой вычисляется поле), вектор
напряжённости E
параллелен
вектору нормали
к поверхности dS.
Таким образом теорема Гаусса для
сферической, равномерно заряженной
поверхности принимает вид
После
несложных преобразований получаем
![]() для
для
![]() (вне сферы S0)
(вне сферы S0)
Д ля
электростатического поля внутри
заряженной сферы
ля
электростатического поля внутри
заряженной сферы
![]()
Поле внутри заряженной частицы равно нулю.
