
- •Министерство образования и науки рф
- •Рабочая программа преподавания дисциплины
- •3. Содержание дисциплины
- •Темы курсовых работ по менеджменту
- •Список литературы
- •Учебная литература дополнительная
- •Лабораторный практикум по дисциплине тема №1 «использование мыслительной техники в управлении»
- •2. Доли и проценты
- •3. Составление системных и квадратных уравнений
- •Ответы и решения
- •1. Общеобразовательные, логические
- •2. Доли проценты
- •3. Coctabлehиe cиctemhыx и квадратных уравнений
- •Практикум по изучению оценки личности
- •Таблички итогов
- •Тема №3. Использование swot- анализа в менеджменте
- •Тема №4. Проектирование и реформирование осу
- •Тема №5. Реализация проектов при ограниченных финансовых ресурсах. Метод «затраты - эффект»
- •2. Динамическое программирование.
- •Задания для выполнения лабораторной работы
- •Контрольные вопросы
- •Тема №6. Применение «венгерского» метода для решения задачи о назначениях реализации проектов
- •2.1. Лабораторная работа № 6
- •2.2. «Венгерский метод»
- •2.3. Задания для выполнения лабораторной работы
- •Контрольные вопросы
- •Библиографический список
- •Тема №7. Деловая игра: использование коллективных методов принятия решений
- •Тема №8. Формирование эффективной команды с использованием психогеометрического метода
- •Применение метода экспертных оценок в задачах принятия решений
- •Введение
- •Тема занятия 1. Оценка согласованности мнений экспертов при выборе наиболее значимых мероприятий
- •Исходные теоретические положения метода экспертных оценок
- •Пример: полный статистический анализ экспертных оценок
- •Тема занятия 2. Выбор мероприятий на основе анализа индивидуальных экспертных мнений
- •2.1 Метод борда
- •2.2 Правило большинства голосов
Контрольные вопросы
1. Какие исходные данные нужны для построения зависимости «затраты - эффект»?
2. Как строится зависимость «затраты - эффект»?
3. Какой анализ можно провести по графику «затраты - эффект»?
Тема №6. Применение «венгерского» метода для решения задачи о назначениях реализации проектов
Цель: получение навыков использования "венгерского" метода для решения задач дискретного программирования.
Время выполнения лабораторной работы: 2 часа.
2.1. Лабораторная работа № 6
МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА
ЗАДАЧИ О НАЗНАЧЕНИЯХ
Стандартная
задача о назначениях формулируется
следующим образом: пусть имеется n
рабочих мест и n
кандидатов на эти места. Назначение
кандидата i на
рабочее место j
связано с затратами
![]() (
(![]() )
на выполнение соответствующего вида
работ. Требуется так распределить
кандидатов по n
рабочим местам, чтобы каждый кандидат
был загружен одним и только одним видом
работ, а суммарные затраты на реализацию
всех видов работ были минимальны. К этой
задаче сводится повседневная задача
распределения рабочей силы между
работами по любым видам работ.
)
на выполнение соответствующего вида
работ. Требуется так распределить
кандидатов по n
рабочим местам, чтобы каждый кандидат
был загружен одним и только одним видом
работ, а суммарные затраты на реализацию
всех видов работ были минимальны. К этой
задаче сводится повседневная задача
распределения рабочей силы между
работами по любым видам работ.
Математическая модель данной задачи имеет следующий вид:
![]() ,
(2.1)
,
(2.1)
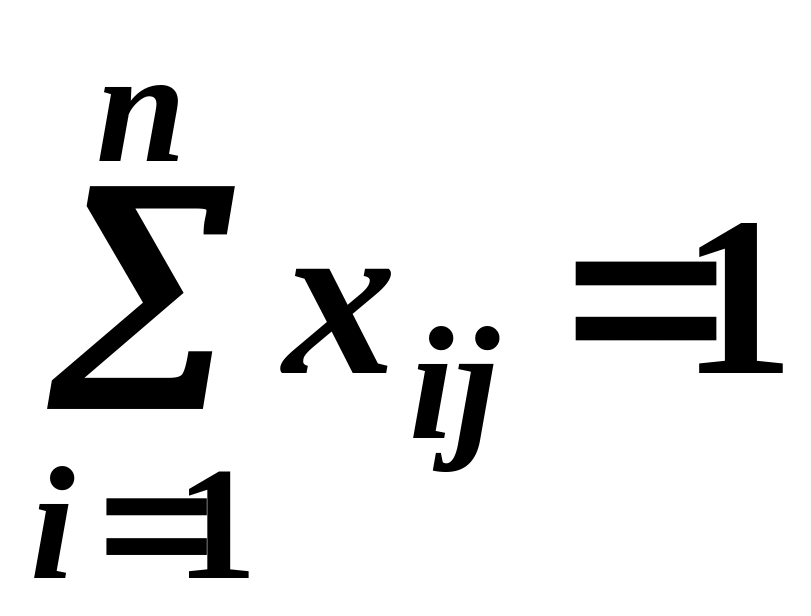 ,
,
![]() ,
(2.2)
,
(2.2)
![]() ,
,
![]() ,
(2.3)
,
(2.3)
![]() .
(2.4)
.
(2.4)
Здесь
![]() =1,
если кандидат i
назначается на рабочее место j,
и
=0
в противном случае.
=1,
если кандидат i
назначается на рабочее место j,
и
=0
в противном случае.
Условия
(2.2) и (2.3) говорят о том, что в каждой
строке и в каждом столбце матрицы
![]() имеется ровно по одной единице. Условие
(2.3) означает, что каждый кандидат может
быть назначен только на одно рабочее
место, а условие (2.2) - что на каждое
рабочее место должен быть назначен один
кандидат.
имеется ровно по одной единице. Условие
(2.3) означает, что каждый кандидат может
быть назначен только на одно рабочее
место, а условие (2.2) - что на каждое
рабочее место должен быть назначен один
кандидат.
Число
различных булевых матриц размерности
![]() ,
у которых в каждом столбце и каждой
строке стоит ровно по одной единице,
равно
,
у которых в каждом столбце и каждой
строке стоит ровно по одной единице,
равно
![]() .
Поэтому решение задачи путем прямого
перебора булевых матриц
,
т.е. вычисления и сравнения значений
функции (2.1) на множестве всех булевых
матриц размерности
,
практически невозможно при сколько-нибудь
больших n. Из – за
этого для её решения применяются
специальные методы, среди которых одним
из наиболее эффективных является
"венгерский" метод.
.
Поэтому решение задачи путем прямого
перебора булевых матриц
,
т.е. вычисления и сравнения значений
функции (2.1) на множестве всех булевых
матриц размерности
,
практически невозможно при сколько-нибудь
больших n. Из – за
этого для её решения применяются
специальные методы, среди которых одним
из наиболее эффективных является
"венгерский" метод.
Перейдём к изложению данного метода и введём следующее определение:
Элементы матрицы называются независимыми, если никакая пара из них не расположена в одном столбце или одной строке.
Таким образом задача о назначениях заключается в нахождении n независимых элементов матрицы С, обладающих минимальной суммой.
2.2. «Венгерский метод»
0-я итерация ( "приведение исходной матрицы C" ).
1.
В каждой строке i
матрицы C ищется
минимальный элемент
![]() ,
который затем вычитается из всех
элементов строки i.
Это обеспечивает получение в каждой
строке нулевых элементов.
,
который затем вычитается из всех
элементов строки i.
Это обеспечивает получение в каждой
строке нулевых элементов.
2.
В преобразованной матрице
![]() ,
полученной после применения к матрице
C
пункта 1, для каждого столбца j
ищется минимальный элемент
,
полученной после применения к матрице
C
пункта 1, для каждого столбца j
ищется минимальный элемент
![]() ,
который затем вычитается из каждого
элемента столбца j.
Это гарантирует получение в каждом
столбце нулевых элементов.
,
который затем вычитается из каждого
элемента столбца j.
Это гарантирует получение в каждом
столбце нулевых элементов.
k-я
итерация (k![]() 1,
"подсчет числа независимых нулей").
На этой итерации используется
справедливость следующего утверждения:
максимальное количество независимых
нулей в матрице совпадает с минимальным
числом строк и столбцов, содержащих
нули матрицы. Поэтому определяется
минимальное число линий, которыми можно
вычеркнуть все нули в матрице.
1,
"подсчет числа независимых нулей").
На этой итерации используется
справедливость следующего утверждения:
максимальное количество независимых
нулей в матрице совпадает с минимальным
числом строк и столбцов, содержащих
нули матрицы. Поэтому определяется
минимальное число линий, которыми можно
вычеркнуть все нули в матрице.
Если
число таких линий n, то
в матрице n независимых нулей,
и по преобразованной матрице
![]() выписываем результат: в матрице
на месте нулевых элементов матрицы
стоят единицы, а на месте ненулевых
элементов - нули. Если этих линий меньше
n, то переходим к k+1-й
итерации.
выписываем результат: в матрице
на месте нулевых элементов матрицы
стоят единицы, а на месте ненулевых
элементов - нули. Если этих линий меньше
n, то переходим к k+1-й
итерации.
k+1-я
итерация. Среди всех незачеркнутых
элементов матрицы ищем
![]() .
Обозначим незачёркнутые элементы
матрицы
через
.
Обозначим незачёркнутые элементы
матрицы
через
![]() ,
зачёркнутые один раз через
,
зачёркнутые один раз через
![]() ,
зачеркнутые дважды -
,
зачеркнутые дважды -
![]() .
Произведём преобразование матрицы по
следующей формуле:
.
Произведём преобразование матрицы по
следующей формуле:
![]() (2.5)
(2.5)
и переходим к k-му этапу.
Пример
Есть 5 мероприятий и 5 фирм, которые могут реализовать эти мероприятия; матрица затрат
![]()
где — затраты, если для реализации i-го мероприятия назначается фирма j.
Распределить реализацию мероприятий по фирмам таким образом, чтобы суммарные затраты были минимальными.
0-я итерация (приведение матрицы):
min
![]()
![]()
![]()
![]()
1 – я итерация (подсчёт числа независимых нулей).


Число независимых нулей равно 4.
2-я
итерация
![]() .
Преобразуем матрицу по формуле (2.5) при
.
Преобразуем матрицу по формуле (2.5) при
![]() :
:
![]()
3-я
итерация Находим минимальное число
линий, которыми можно перечеркнуть все
нули в матрице
![]() (число независимых нулей):
(число независимых нулей):
![]()

Число независимых нулей в матрице равно 5. В следующей матрице выделены независимые нули:

Соответствующая матрица «назначений» имеет вид:
![]()
т.е.
для того, чтобы получить минимальные
затраты
![]() = 12 + 7 + 14 + 22 + 18 = 73, необходимо, чтобы
1-е мероприятие выполнялось 1-й фирмой;
2-е мероприятие выполнялось 4 – й фирмой,
3 – е мероприятие – 2 – й фирмой, 4 – е
мероприятие – 3 – й фирмой, а 5 – е
мероприятие – 5 – й фирмой.
= 12 + 7 + 14 + 22 + 18 = 73, необходимо, чтобы
1-е мероприятие выполнялось 1-й фирмой;
2-е мероприятие выполнялось 4 – й фирмой,
3 – е мероприятие – 2 – й фирмой, 4 – е
мероприятие – 3 – й фирмой, а 5 – е
мероприятие – 5 – й фирмой.
