
- •Глава 4. Матричные игры §1. Основные понятия теории игр
- •1. Конфликтные ситуации
- •2. Основные понятия теории игр
- •1. Приведение игры к матричной форме
- •2. Примеры матричных игр
- •3. Максиминная и минимаксная стратегии игроков
- •Максиминная стратегия, принцип максимина
- •Минимаксная стратегия
- •4. Седловая точка матричной игры
- •Нахождение седловой точки платежной матрицы
- •5. Оптимальные стратегии, их устойчивость
- •§3. Матричные игры в смешанных стратегиях
- •1. Понятие смешанной стратегии
- •2. Функция выигрыша игры в смешанных стратегиях
- •Реализация смешанной стратегии
- •3. Оптимальные стратегии, решение игры
- •5. Свойства оптимальных стратегий
- •Решение игры в смешанных стратегиях
- •Доминирование стратегий
- •§4. Графический метод решения матричной игры
- •1. Игра
- •2. Игра
- •§5. Решение матричной игры путем ее сведения к задаче линейного программирования
- •Контрольные вопросы к главе
5. Свойства оптимальных стратегий
Оптимальные стратегии имеют ряд свойств,
которые используются в различных методах
их нахождения. Так как функция выигрыша
![]() линейна по каждому из своих аргументов
при фиксированном значении другого
аргумента, то из условия (3.4) следует
линейна по каждому из своих аргументов
при фиксированном значении другого
аргумента, то из условия (3.4) следует
Теорема 3.3 (критерий оптимальности стратегий). Пусть ν — цена игры с платежной матрицей А. Тогда
а) вектор
![]() будет оптимальной стратегией игрока 1
в том и только в том случае, если для
любой чистой стратегии
будет оптимальной стратегией игрока 1
в том и только в том случае, если для
любой чистой стратегии
![]() игрока 2 выполняется неравенство
игрока 2 выполняется неравенство
![]() ; (3.5)
; (3.5)
б) вектор
![]() будет оптимальной стратегией игрока 2
в том и только в том случае, если для
любой чистой стратегии
будет оптимальной стратегией игрока 2
в том и только в том случае, если для
любой чистой стратегии
![]() игрока 1 выполняется неравенство
игрока 1 выполняется неравенство
![]() . (3.6)
. (3.6)
Таким образом, при проверке оптимальности смешанной стратегии игрока можно ограничиться чистыми стратегиями его противника.
В оптимальной смешанной стратегии
обычно используется лишь часть чистых
стратегий игрока. Будем называть чистую
стратегию
![]() игрока 1 (игрока 2) активной, если она
входит в его оптимальную стратегию с
положительной вероятностью (частотой),
т.е.
игрока 1 (игрока 2) активной, если она
входит в его оптимальную стратегию с
положительной вероятностью (частотой),
т.е.
![]() .
.
Свойства активных стратегий описывает следующая теорема.
Теорема 3.4. Пусть { , , ν} — решение матричной игры. Тогда
а) если
![]()
б) если
![]() .
.
Иными словами, если чистая стратегия игрока является активной, то его выигрыш в ситуации, образованной этой чистой стратегией и оптимальной стратегией другого игрока, равен цене игры.
Решение игры в смешанных стратегиях
Теорему 3.4 можно использовать для нахождения решения игры, в которой каждый из игроков имеет две чистых стратегии.
Пример 3.2. Найдем решение игры с платежной матрицей из примера 3.1:
|
В1 |
В2 |
|
A1 |
2 |
3 |
х1 |
A2 |
4 |
2 |
х2 |
|
y1 |
y2 |
|
Так как максимин = 2, а минимакс = 3, то эта игра не имеет седловой точки, а значит и решения в чистых стратегиях. Найдем ее решение в смешанных стратегиях. Известно, что в любой игре 2х2, не имеющей седловой точки, все чистые стратегии, входящие в оптимальные стратегии игроков, являются активными.
Пусть (х1, х2) и (у1, у2) — оптимальные стратегии игроков, а ν — цена игры. Тогда из теоремы 3.4 следует, что выигрыш игрока 1 в ситуации, образованной его оптимальной стратегией (х1, х2) и первой чистой стратегией (1, 0) игрока 2, равен цене игры, т.е. 2х1 + 4х2 = ν.
Используя эту теорему в ситуации, когда игрок 1 применяет свою оптимальную стратегию (х1, х2), а игрок 2 — свою вторую чистую стратегию (0, 1) получаем, что 3х1 + 2х2 = ν. Кроме этого имеем, что х1 + х2 = 1, как сумма вероятностей.
Таким образом, оптимальную стратегию игрока 1 и цену игры можно найти из системы уравнений:
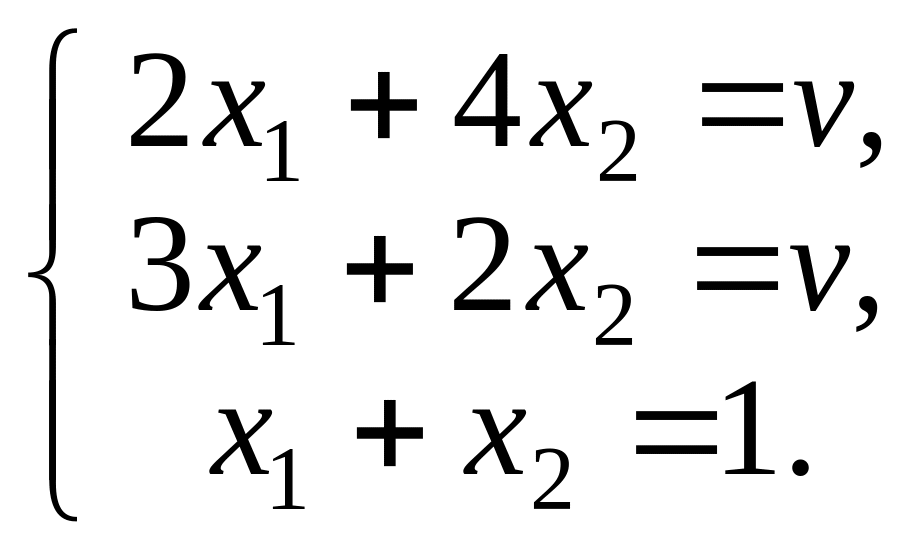
Вычтя из первого уравнения второе, получим, что -х1 + 2х2 = 0. Следовательно, х1 = 2х2. Подставляя в третье уравнение, получим, что х1 = 2/3, х2 = 1/3 и ν = 8/3.
Для определения оптимальных стратегий игрока 2 снова используем теорему 3.4 в ситуации, когда игрок 1 применяет свою первую чистую стратегию (1, 0), а игрок 2 — свою оптимальную стратегию (у1, у2). Так как цена игры равна 8/3, то получаем уравнение: 2у1 +3у2 = 8/3.
Поскольку у1 + у2 = 1, как сумма вероятностей, оптимальную стратегию игрока 2 можно найти из системы уравнений:
![]()
Ее решение: у1 = 1/3 и у2 = 2/3. Значит, решение игры:
х* = (1/3, 2/3); у* = (1/3, 2/3); ν = 8/3.
Пример 3.3. Найдем решение игры в орлянку. Ее матрица имеет вид:
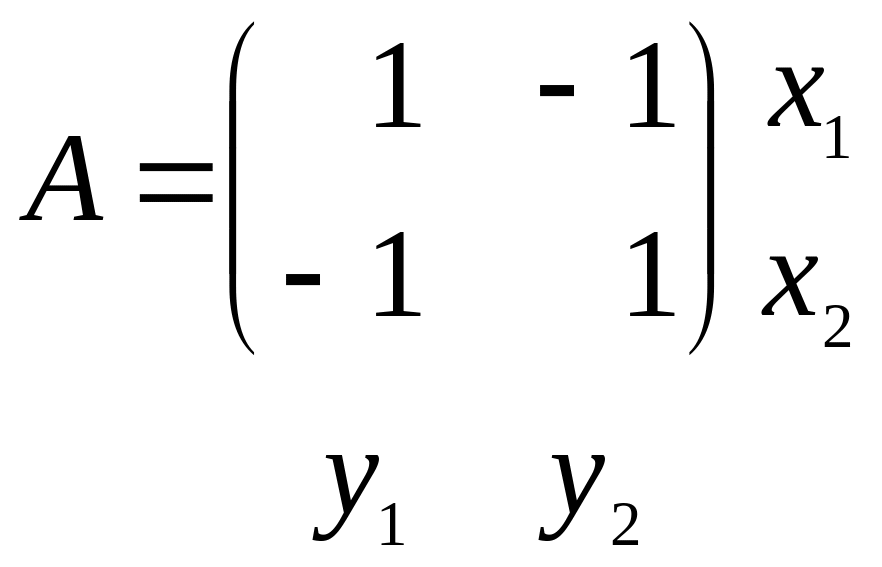
Оптимальную стратегию игрока 1 и цену игры найдем из системы уравнений:
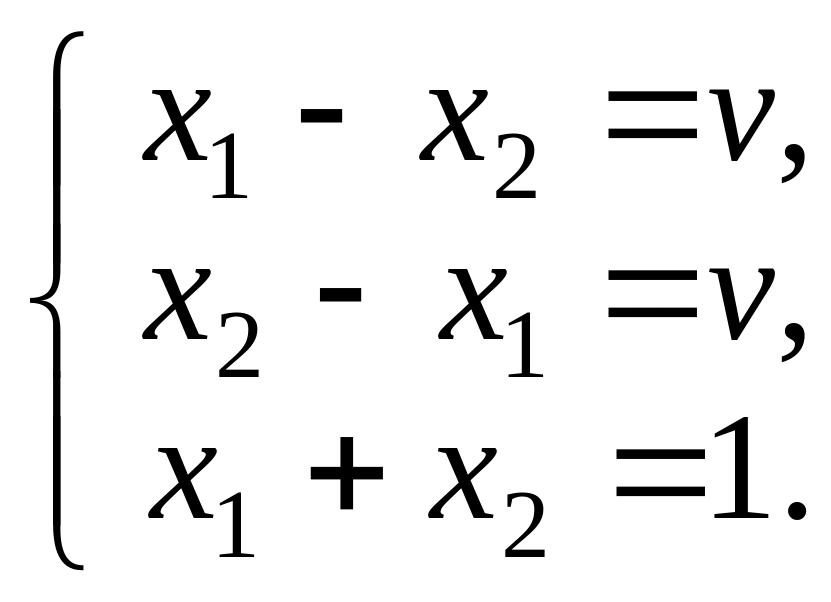
Вычтя из первого уравнения второе,
получим, что
![]() .
Следовательно,
.
Следовательно,
![]() ,
а ν = 0.
,
а ν = 0.
Оптимальную стратегию игрока 2 находим из системы уравнений:
![]()
Ее решение:
![]() .
Таким образом, игра в орлянку имеет
решение:
.
Таким образом, игра в орлянку имеет
решение:
![]() ,
,
![]() и ν = 0,
и ν = 0,
что полностью соответствует полученным ранее результатам.
Из теоремы 3.4 вытекает следующее правило отбраковки чистых стратегий игрока.
Теорема 3.5.
Пусть ν — цена
игры, вектор
![]() — оптимальная смешанная стратегия
игрока 1, а вектор
— оптимальная смешанная стратегия
игрока 1, а вектор
![]() — оптимальная смешанная стратегия
игрока 2. Тогда
— оптимальная смешанная стратегия
игрока 2. Тогда
1) если
![]() ,
,
2) если![]() .
.
Иными словами, если выигрыш (проигрыш) игрока 1 (игрока 2) в ситуации, образованной его чистой стратегией и оптимальной стратегией другого игрока, меньше (больше) цены игры, то такая чистая стратегия не может быть активной. В любой оптимальной смешанной стратегии вероятность ее использования равна нулю. Такие чистые стратегии могут быть исключены из рассмотрения без изменения множества решений игры. Это позволяет уменьшить размерность игры и упрощает нахождение ее решения.
