1. Приведение игры к матричной форме

Рассмотрим конечную антагонистическую игру. Будем считать, что число стратегий игрока 1 равно m, а число стратегий игрока 2 равно n. Обозначим = {А₁, А₂,…, А_m} — множество стратегий игрока 1, а  = {B₁, B₂,… , B_n} — множество стратегий игрока 2. Эти стратегии называют чистыми.

Партия в такой игре сводится к тому, что игроки выбирают свои стратегии, а затем подсчитываются их выигрыши. Отметим, что, выбирая свою стратегию, ни один из игроков точно не знает, какой выбор сделает его противник, хотя и может делать гипотезы относительно его поведения.

Обозначим Н(х, у) — выигрыш¹ игрока 1, если он выбрал стратегию х, а игрок 2 — стратегию у. Тем самым, на множестве всех пар (х, у), где определена функция Н, которая называется функцией выигрыша игрока 1 или просто функцией выигрыша.

Так как игра является антагонистической, то выигрыш игрока 2 составит величину -Н(х, у) или, что то же самое, его проигрыш будет равен Н(х, у). Ясно, что игроку 1 выгодно, чтобы значение Н(х, у) было как можно больше, а игрок 2 хочет сделать его как можно меньше. Таким образом, при выборе своих стратегий оба игрока имеют дело с одной и той же функцией Н, но игрок 1 стремится ее максимизировать, а игрок 2 — минимизировать.

Обозначим а_ij = Н(A_i, B_j) — выигрыш игрока 1 (проигрыш игрока 2), если он использует стратегию А_i, а игрок 2 — стратегию B_j. Тогда можно определить матрицу А размерности mxn, которая называется матрицей выигрышей или платежной матрицей.

.

В этой матрице строка с номером i соответствует стратегии А_i игрока 1 и содержит значения его выигрышей в зависимости от ответа игрока 2. Столбец с номером j соответствует стратегии В_j игрока 2 и содержит его проигрыши в зависимости от ответа игрока 1.

Если такая матрица составлена, то говорят, что игра приведена к матричной форме. К этой форме можно привести любую конечную антагонистическую игру. Поэтому такие игры называют матричными.

В дальнейшем мы обычно будем представлять стратегии игроков в платежной матрице в явном виде. Тогда она будет выглядеть так:

	В1	В2	…	Вn
A1	a11	a12	…	a1n
A2	a21	a22	…	a2n
…	…	…	…	…
Am	am1	аm2	…	amn

После приведения игры к матричной форме партия состоит в выборе игроком 1 строки, а игроком 2 — столбца этой матрицы. Выигрыш игрока 1 и, соответственно, проигрыш игрока 2 равен элементу, находящемуся на их пересечении.

2. Примеры матричных игр

Рассмотрим несколько конфликтных ситуаций, моделями которых являются матричные игры.

Пример 2.1 (конкуренция фирм на рынке). Две фирмы конкурируют на рынке. Первая фирма (игрок 1) выпускает три вида продукции, а вторая фирма (игрок 2) — четыре вида продукции. Каждая из них хотела бы продавать на рынке один из своих товаров. Однако конкурентоспособность их продукции различна и в зависимости от того, какой товар будет продавать ее конкурент, это может привести как к получению прибыли, так и к убыткам.

Предположим, что величина прибыли фирмы всегда равна убыткам ее конкурента, т.е. суммарная прибыль обеих фирм всегда равна нулю. Тогда описанную ситуацию можно смоделировать как антагонистическую игру. Будем считать, что выигрыш игрока (фирмы) равен размеру полученной им прибыли и известна матрица А = (а_ij) выигрышей первой фирмы в зависимости от ситуации, сложившейся на рынке.

.

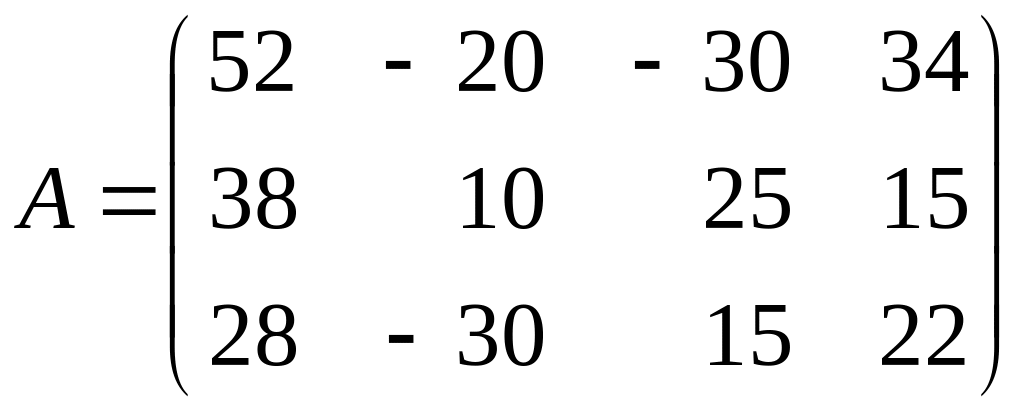В i-й строке этой матрицы находятся размеры а_ij прибыли (млн. руб.), которую получит первая фирма при продаже i-го товара, если вторая фирма будет представлена на рынке j-м товаром. Отрицательная величина а_ij говорит о том, что в данной ситуации первая фирма терпит убытки, а прибыль получает вторая фирма.

Игрок 1 (первая фирма) имеет три чистых стратегии {А₁, А₂, А₃}, где А_i — продажа на рынке i-го вида продукции, соответствующие строкам матрицы А. Игрок 2 (вторая фирма) имеет четыре чистых стратегии {В₁, В₂, В₃, В₄}, где B_j — продажа на рынке j-го вида продукции, которые соответствуют столбцам матрицы А. Нужно определить оптимальную стратегию каждой из фирм.

Пример 2.2 (учет потребительского спроса). Фирма планирует выпустить новую модель одежды. Спрос потребителей на эту модель точно не известен, но можно предположить, что его величина характеризуется четырьмя возможными состояниями (В₁, В₂, В₃, В₄). С учетом этих состояний проводится анализ трех возможных вариантов выпуска модели (А₁, А₂, А₃). Каждый из них требует определенных затрат и обеспечивает различный эффект. Прибыль (млн. руб.), которую получит фирма при выборе данного варианта выпуска модели и соответствующем уровне спроса определяется матрицей:

.

Нужно определить, какую модель следует выпускать фирме.

Эту ситуацию также можно рассматривать как игру двух лиц, в которой игрок 1 — фирма, а игрок 2 — покупательский спрос. Чистыми стратегиями игрока 1 являются варианты выпуска моделей {А₁, А₂, А₃}, которым соответствуют строки матрицы А. Чистые стратегии игрока 2 — уровни спроса на продукцию фирмы {В₁, В₂, В₃, В₄} (столбцы матрицы А). Если игрок 1 выберет строку i , а игрок 2 — столбец j матрицы А, то выигрыш игрока 1 (проигрыш игрока 2) будет равен значению элемента а_ij.

Пример 2.3 (игра в орлянку). Игроки одновременно показывают друг другу по одной монете. Если их выборы совпадают, т.е. оба игрока показывают «орел» или «решку», то игрок 1 выигрывает единицу. В противном случае такую же величину выигрывает игрок 2. Предполагается, что игра повторяется несколько раз. Нужно определить, какой тактики должен придерживаться каждый игрок, чтобы максимизировать свой средний выигрыш.

В этой игре игрок 1 имеет только два возможных хода: показать «орел» (А₁) или показать «решку» (А₂). Они являются его чистыми стратегиями. Такие же чистые стратегии (В₁ — «орел» и В₂ — «решка») имеет и игрок 2. Матрица этой игры имеет такой вид:

.

Игрок 1 выбирает строку, а игрок 2 — столбец матрицы А. Пусть, например, игрок 1 выбрал первую строку: показал «орел». Тогда, если игрок 2 выбрал первый столбец («орел»), то игрок 1 выигрывает величину а₁₁ = 1, а игрок 2 проигрывает эту величину.

Если же игрок 2 выбрал второй столбец («решка»), то игрок 1 выигрывает величину а₁₂ = -1, т.е. проигрывает 1, а игрок 2 выигрывает 1. Аналогично определяется результат партии, если игрок 1 выберет вторую строку.