2. Игра

Предположим, что первый игрок имеет m чистых стратегий, а второй игрок — две чистых стратегии, т.е. , а .

Тогда платежная матрица игры выглядит так:

.

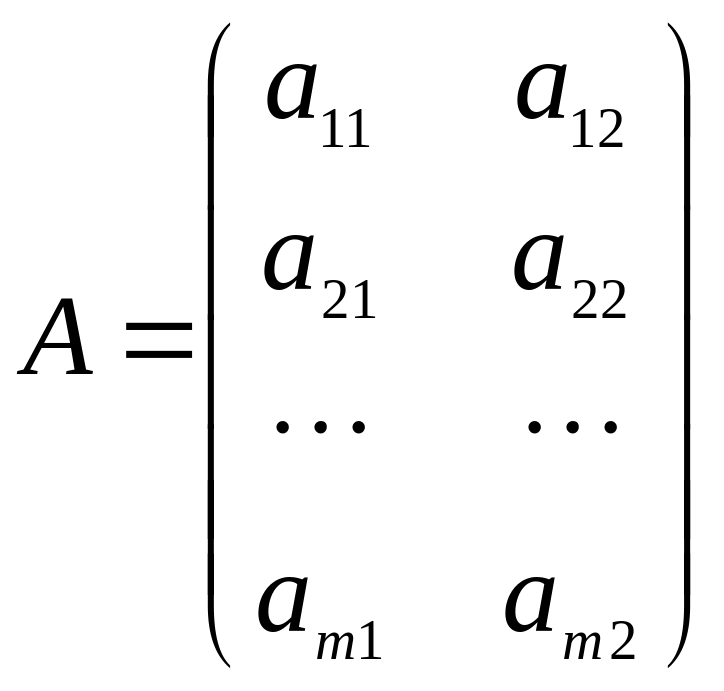Множество смешанных стратегий игроков имеет следующий вид:

• для игрока 1 — ;

• для игрока 2 — .

Обозначим — проигрыш игрока 2 в ситуации, когда он выбрал смешанную стратегию , а игрок 1 — свою чистую стратегию . Тогда ясно, что

.

Обозначим — максимально возможный проигрыш игрока 2 при выборе им стратегии . По теореме 3.1 для игрока 2 оптимальной будет стратегия , которой соответствует значение , дающее минимум функции на отрезке [0, 1], т.е.

.

Функция будет выпуклой кусочно-линейной функцией на отрезке [0, 1]. Она является верхней огибающей семейства прямых { }; а ее минимум равен цене игры, т.е. .

По теореме 3.5 все стратегии игрока 1, для которых < , могут быть отброшены. Как правило, активными будут лишь две стратегии этого игрока, что также позволяет свести решение игры к случаю .

Использование графического метода в этом случае аналогично описанному выше. Проиллюстрируем его на следующем примере.

Пример 4.2. Нужно найти решение игры, задаваемой матрицей

.

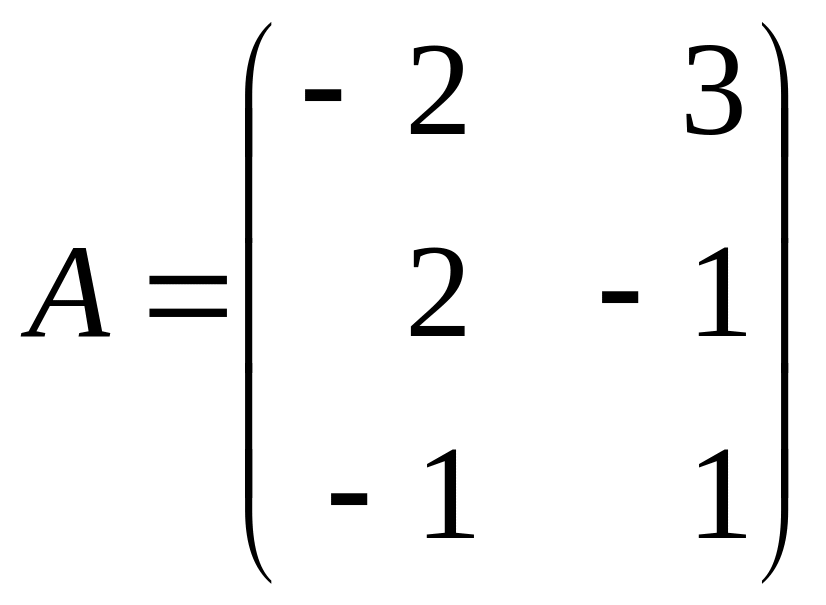Проверим, есть ли у этой игры решение в чистых стратегиях. Для этого найдем и . Так как они не равны друг другу, то решения в чистых стратегиях нет.

На оси Ot плоскости tOR отложим единичный отрезок [0, 1]. Каждой его точке t соответствует смешанная стратегия игрока 2. Затем через точки 0 и 1 проведем линии, перпендикулярные оси Ot.

На первом перпендикуляре, совпадающем с осью OR, отложим значения элементов первого столбца матрицы А — проигрыши игрока 2 при выборе им чистой стратегии . На втором перпендикуляре отложим значения элементов второго столбца — проигрыши игрока 2 при выборе им чистой стратегии .

Затем соединим отрезками прямых точки на перпендикулярах, соответствующие чистым стратегиям игрока 1 — строкам матрицы А. Эти отрезки прямых являются графиками функций , задаваемых следующими уравнениями:

П

Рис. 4.2. Графический метод решения игры

остроим их верхнюю огибающую — график функции . На рис. 4.2 она представлена ломаной АВС. Ее точка В, имеющая минимальную ординату, является графическим решением игры.

Из рисунка видно, что точка В лежит на пересечении отрезков прямых  и . Значит, активными стратегиями игрока 1 являются стратегии и  . Стратегия в его оптимальной смешанной стратегии не используется, т.е. . Поэтому третью строку матрицы А можно вычеркнуть и рассмотреть игру с платежной матрицей

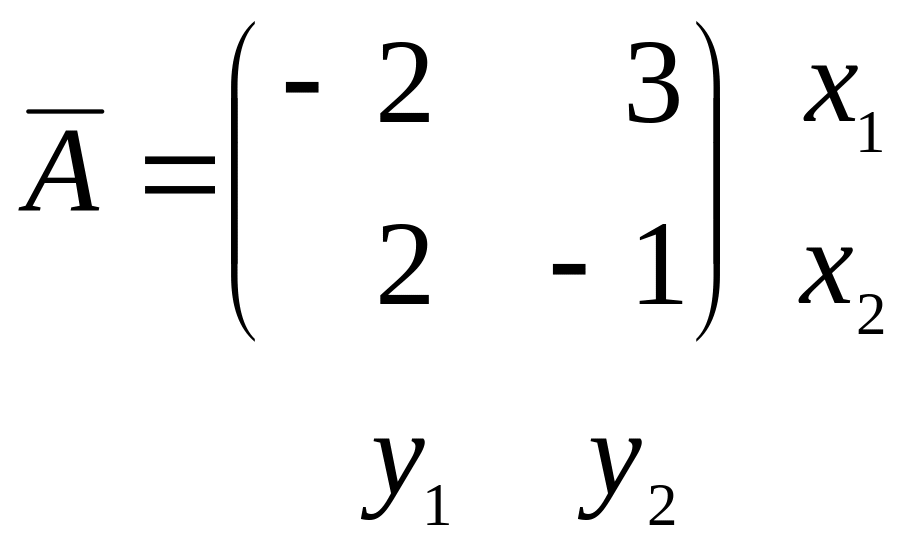
Для определения цены этой игры и оптимальной смешанной стратегии игрока 1 следует решить систему уравнений:

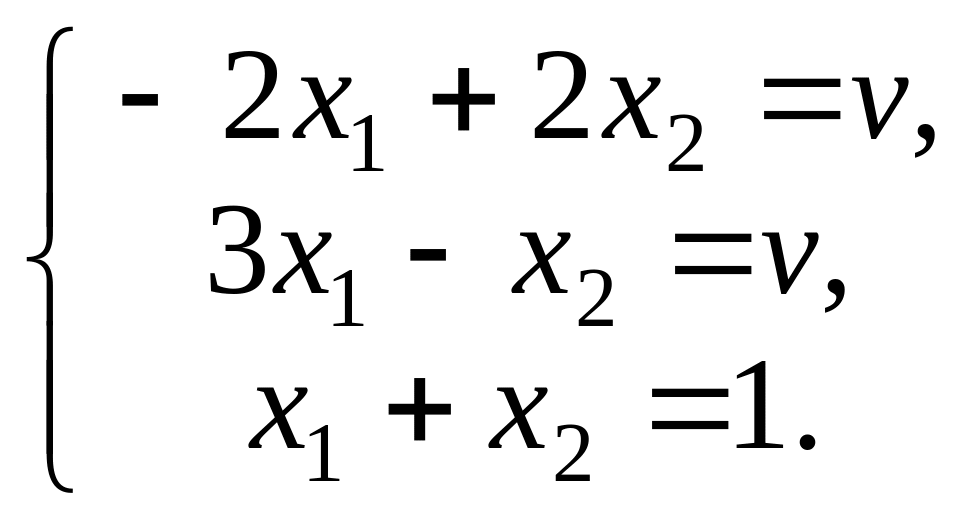
Вычтя из первого уравнения второе, получим, что . Значит, , а .

Для нахождения коэффициентов активных стратегий игрока 2 нужно решить систему уравнений:

Ее решение: . Итак, исходная игра имеет решение:

.

§5. Решение матричной игры путем ее сведения к задаче линейного программирования

Общим методом решения матричной игры, не имеющей седловой точки, является ее сведение к задаче линейного программирования. Пусть игрок 1 имеет m чистых стратегий, а игрок 2 — n чистых стратегий. Тогда матрица игры имеет вид:

	В1	В2	…	Вn
A1	a11	a12	…	a1n	х1
A2	a21	a22	…	a2n	х2
…	…	…	…	…	…
Am	am1	аm2	…	Amn	хm
	y1	y2	…	уn

Для нахождения оптимальной стратегии игрока 1 и цены игры следует решить задачу линейного программирования.

Задача игрока 1

ν → max, (5.1)

(5.2)

, (5.3)

. (5.4)

В этой задаче m + 1 переменная и n + 1 ограничение общего вида. Переменными в ней являются цена игры ν и вектор смешанных стратегий х = (х₁,…, х_m) игрока 1. Переменная ν может быть любого знака, а все компоненты вектора х должны быть неотрицательны, причем их сумма равна единице. Ограничения (5.2) — это условия оптимальности смешанной стратегии х (см. теорему 3.3). Ищется максимальное значение переменной ν (цены игры).

Аналогично, нахождение оптимальной стратегии игрока 2 и цены игры можно свести к решению следующей задачи линейного программирования.

Задача игрока 2

w → min, (5.5)

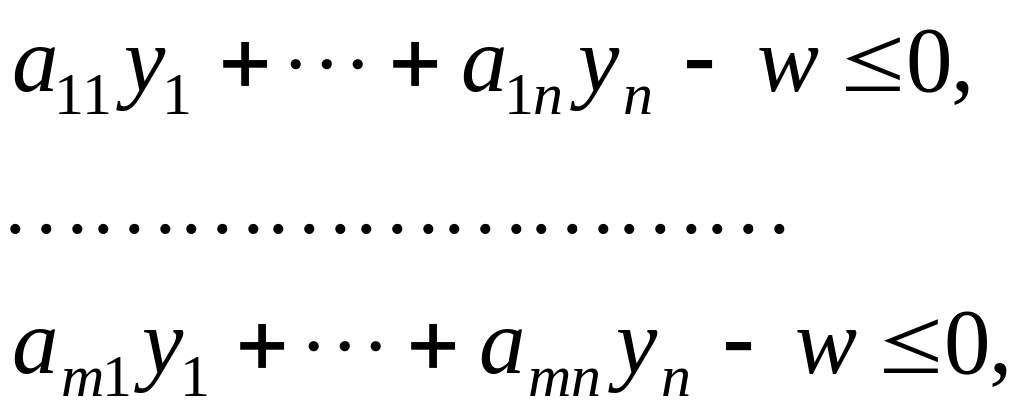(5.6)

, (5.7)

. (5.8)

Она содержит n + 1 переменную и m + 1 ограничение общего вида. Ее переменные: вектор стратегий у = (у₁,…, у_n) игрока 2 и цена игры w. Неравенства (5.6) — это условия оптимальности смешанной стратегии у (см. теорему 3.3). Ищется минимальное значение переменной w.

Легко проверить, что эти задачи являются двойственными. Поэтому для нахождения решения игры достаточно решить любую из них. Если найдено решение задачи 1, то вектор оптимальных оценок ограничений (5.2) будет оптимальной смешанной стратегией игрока 2. Соответственно, если найдено решение задачи 2, то вектор оптимальных оценок ограничений (5.6) будет оптимальной смешанной стратегией игрока 1.

Пример 5.1. Пусть дана матричная игра с платежной матрицей

.

Тогда пара двойственных задач, эквивалентная этой матричной игре, имеет такой вид:

Задача игрока 1:

,

Задача игрока 2:

w → min,

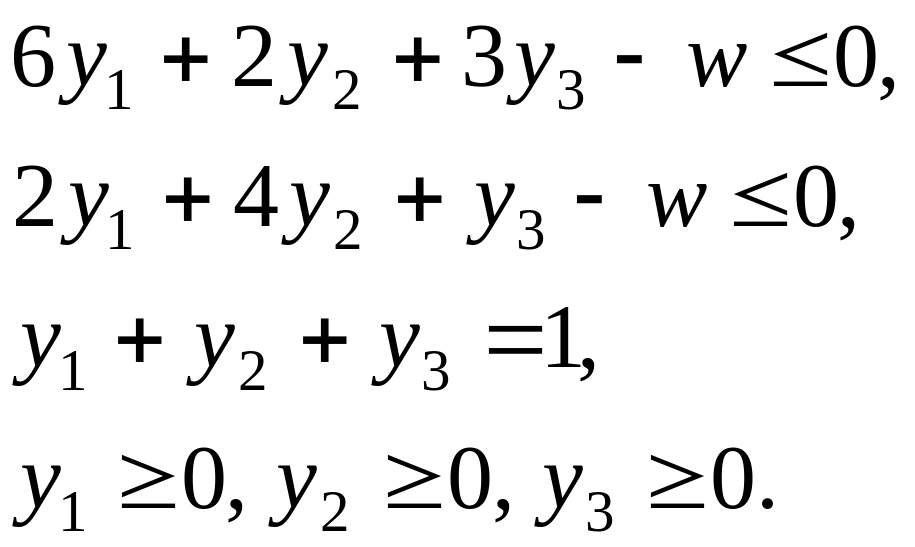
Решив задачу 1 симплекс-методом, получим следующие результаты:

х^* = (0.75, 0.25); у^* = (0, 0.5, 0.5); v^* = 2.5.

Здесь компоненты вектора у^* — оптимальной смешанной стратегии игрока 2 — являются оптимальными оценками общих ограничений-неравенств в задаче 1.

Таким образом, решение матричной игры сводится к решению пары двойственных задач линейного программирования. Можно доказать, что для любой платежной матрицы эти задачи всегда имеют оптимальные решения. Поэтому справедливость основной теоремы матричных игр о разрешимости любой игры в смешанных стратегиях является следствием теоремы двойственности для задачи линейного программирования.

Оказывается, что если задача линейного программирования имеет оптимальное решение, то ей можно сопоставить матричную игру, в которой множества оптимальных стратегий игроков совпадают с множествами оптимальных планов исходной и двойственной ей задачи линейного программирования. Таким образом, между матричными играми и задачами линейного программирования существует тесная связь, и для нахождения решения задачи, принадлежащей одному из этих классов, можно использовать методы, созданные для решения задач из другого класса.