Аксиомы вероятности

В математике даётся следующее определение понятия вероятность: каждому событию A ставится в соответствие вещественное число P(A), удовлетворяющее следующим трём аксиомам:

1. Неотрицательность. P(A)0,

2. Нормированность. P(Ω)=1,

3. Аддитивность (аксиома сложения). Если A_iA_j= при i≠j, то 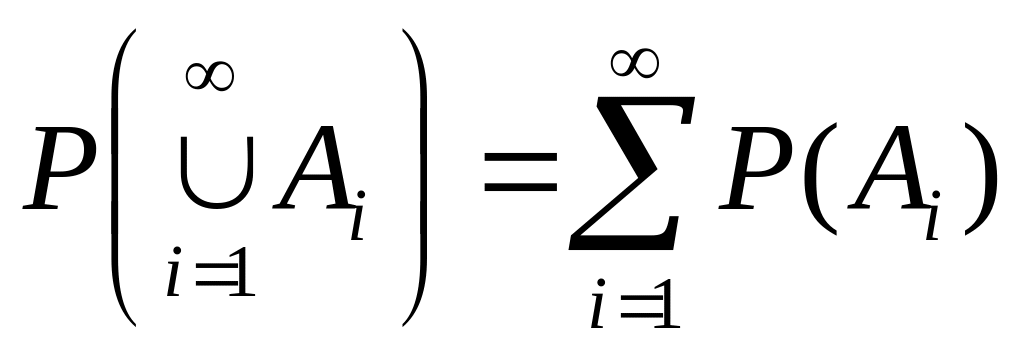, или то же самое в развёрнутом виде: P(A₁A₂A₃…A_n…)=P(A₁)+P(A₂)+P(A₃)+…+P(A_n)+… . В частности для двух событий: если AB=, то P(AB)=P(A)+P(B). Или то же самое словами: Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий.

Теперь возникает закономерный вопрос гуманитария: «Почему так, и какая связь этого с житейским пониманием вероятности». Выше было установлено, что вероятность приближённо равна частоте (при достаточно большом количестве испытаний) и «приближается» к ней при неограниченном увеличении числа испытаний (я всё-таки глагол «приближается» пишу в кавычках, так как ни о какой монотонности убывания величины |f–p| не может быть и речи). И житейские представления о вероятности, кроме как с понятием частоты, связать не с чем. Убедимся в выполнении свойств частоты, соответствующих трём аксиомам вероятности.

1. Частота равна отношению двух неотрицательных чисел (числа наступивших событий и количества испытаний) и не может быть отрицательной.

2. Если событие достоверное, то оно происходит при любом испытании. Число появлений события совпадает с числом экспериментов. Оказываются равными числитель и знаменатель дроби, равной частоте. Поэтому частота появления достоверного события равна единице.

3. Разберём простейший случай. Пусть событий не бесконечно много, а всего два. Пусть поведено N испытаний, событие A произошло K раз, а событие B наступило L раз. Причём, поскольку A и B несовместные события, то одновременно они произойти не могли, и, следовательно, хотя бы одно из этих событий наступило столько же раз, сколько наступило ровно одно из них, то есть (K+L) раз. Тогда частота наступления события A равна K/N, частота наступления события B равна L/N, а частота наступления хотя бы одного из этих событий равна (K+L)/N. И действительно справедливо равенство K/N+L/N=(K+L)/N.

Теперь остаётся надеяться (а математик аксиомы постулирует, не испытывая никаких психологических проблем), что у вероятности свойства такие же как и у частоты.

Следствия из аксиом вероятности

1. Вероятность противоположного события P(A ) = 1 – P(A).

Доказательство. Поскольку A A =  и A A = Ω, то по нормированности вероятности и аксиоме сложения: 1 = P(Ω) = P(A A) = P(A) + P(A ). Следовательно P(A ) = 1 – P(A), как впрочем и P(A) = 1– P(A ). Это свойство часто используется при нахождении вероятностей реализации хотя бы одного из некоторого набора событий. Обычно гораздо проще найти вероятность противоположного события (заключающееся в том, что должны будут одновременно реализоваться все события из этого набора) и вычесть её из единицы.

2. Вероятность невозможного события P()=0.

Д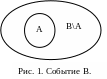 оказательство. Поскольку  = Ω\Ω =Ω, то по вероятности противоположного события P(Ω )=1 – P(Ω)=1–1=0.

3. Монотонность вероятности. Если AB, то P(A) ≤ P(B).

Доказательство. Разобьём событие B на два несовместных события A и B\A (см. рис. 1). Теперь из A(B\A)= и A(B\A)=B по аксиоме сложения следует, что P(B)=P(A)+P(B\A). Но по неотрицательности вероятности P(B\A) ≥ 0 и поэтому P(B) = P(A) + P(B\A) ≥ P(A) + 0 = P(A). Это свойство названо монотонностью, поскольку напоминает определение возрастающей функции на промежутке, согласно которому большему значению аргумента соответствует большее значение функции.

4. Ограниченность вероятности. P(A) ≤ 1.

Доказательство. Любое событие AΩ. По свойству монотонности и аксиоме нормированности P(A) ≤ P(Ω) = 1.

5. П 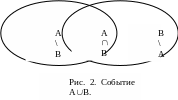равило сложения. P(AB)=P(A)+P(B)–P(AB). В отличие от аксиомы сложения здесь события A и B какие угодно (в аксиоме сложения они были обязательно несовместные).

Доказательство. Разобьём событие AB на три несовместных события A\B, B\A и AB (см. рис. 2). Теперь из того, что AB=(A\B)(B\A)(AB), и попарной несовместности этих трёх событий, то есть из того, что (A\B)(B\A)=, (A\B)(AB)= и (B\A)(AB)=, согласно аксиоме сложения следует, что P(AB)=P(A\B)+P(B\A)+P(AB). Заметим, что при этом разбиении, событие A автоматически окажется разбитым на два несовместных события: A\B и AB. И из того, что (A\B)(AB)= и A=(A\B)(AB) по аксиоме сложения следует, что P(A)=P(A\B)+P(AB). Аналогичное явление произойдёт и с событием B. Оно тоже будет разбито на два несовместных события: B\A и AB. И из того, что (B\A)(AB)= и B=(B\A)(AB) по аксиоме сложения следует, что P(B)=P(B\A)+P(AB). Теперь из трёх полученных равенств с помощью арифметики можно доказать требуемое утверждение: Подставляя второе и третье равенства, в первое, получим

P(AB)=P(A)–P(AB)+P(B)–P(AB)+ P(AB)= P(A)+P(B)–P(AB).

6. Неравенство для совокупности событий. 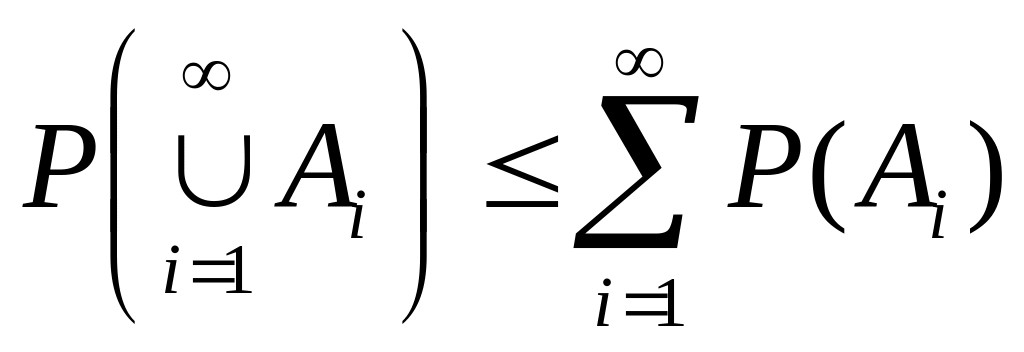, или то же самое в развёрнутом виде: P(A₁A₂A₃…A_n…) ≤ P(A₁)+P(A₂)+P(A₃)+…+P(A_n)+… . В частности для двух событий: P(AB) ≤ P(A)+P(B).

Доказательство проведём только для двух событий. По правилу сложения P(AB)=P(A)+P(B)–P(AB). По неотрицательности вероятности P(AB) ≥ 0. Следовательно, P(AB)=P(A)+P(B)–P(AB) ≤ P(A)+P(B)–0=P(A)+P(B). Напомним, что равенство наступает при AB=.