2. Схема Бернулли
● Вероятности
В чем состоит схема Бернулли? Запишите формулу для вероятности
успехов в серии
испытаний по схеме Бернулли и
приведите пример ее применения.
Выведите формулу для вероятности успехов в серии испытаний по схеме Бернулли.
● Наиболее вероятное число успехов
Выведите формулу для наиболее вероятного числа успехов в серии испытаний по схеме Бернулли.
Пусть – вероятность успехов в серии независимых испытаний с вероятностью успеха в каждом испытании. При каком вероятность достигает максимума? Совпадает ли это число с математическим ожиданием количества успехов? Чему равна сумма
?
Может ли наиболее вероятное число успехов в схеме Бернулли отличаться от математического ожидания числа успехов на 2? Ответ обоснуйте.
● Вероятности при больших значениях
Запишите локальную приближенную формулу Лапласа, приведите основные свойства функции Гаусса
и укажите ее график. При каких
условиях данная формула дает хорошее
приближение? Какие условия применимости
отличают эту формулу от приближенной
формулы Пуассона?
Запишите интегральную приближенную формулу Лапласа и приведите основные свойства функции Лапласа
.
При каких условиях данная формула
дает хорошее приближение?
Укажите выражение для функции Лапласа . Докажите нечетность функции и нарисуйте график
.
Чему равно
?
Используя интегральную приближенную формулу Лапласа, выведите формулу для оценки отклонения относительной частоты события от вероятности наступления в одном опыте.
● Предельная теорема Пуассона
Сформулируйте и докажите предельную теорему Пуассона.
Запишите приближенные формулы Пуассона. При каких условиях они дают хорошее приближение? Приведите пример их применения.
3. Дискретные случайные величины
● Функция распределения случайной величины
Что такое случайная величина? Что такое дискретная случайная величина? Что называется функцией распределения случайной величины? Приведите пример функции
,
которая является функцией распределения
некоторой дискретной случайной
величины
,
объясните, почему это так и постройте
ее график.Сформулируйте основные свойства функции распределения случайной величины и продемонстрируйте их на примере.
Может ли график функции распределения быть прямой линией? Ответ обоснуйте.
Что такое дискретная случайная величина? Может ли таблица
рассматриваться как закон распределения дискретной случайной величины?
Дана дискретная случайная величина с законом распределения
Что является ее
функцией распределения
?
Постройте график
и опишите его точки разрыва. Как
вычисляется вероятность
?
● Типичные законы распределения дискретных случайных величин
Что называется геометрическим распределением с параметром ? Приведите пример опытов, в котором определена случайная величина, распределенная по геометрическому закону с параметром .
Что называется биномиальным распределением с параметрами и ? Приведите пример опытов, в котором определена случайная величина, распределенная по биномиальному закону.
Какой закон распределения называется законом Пуассона? В чем состоит связь этого закона с предельной теоремой Пуассона (приближенной формулой Пуассона)?
● Независимые дискретные случайные величины
Как определяется независимость случайных величин? Игральную кость бросают
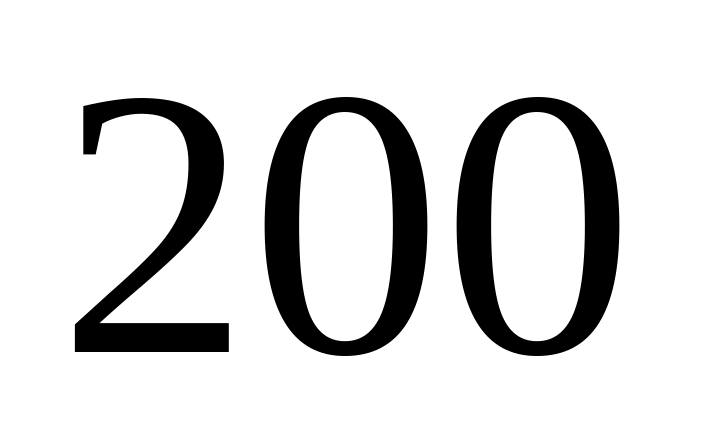раз. Пусть
– число выпадений грани
;
– число выпадений грани
.
Будут ли зависимыми случайные
величины
и
?
Ответ обоснуйте.
Пусть
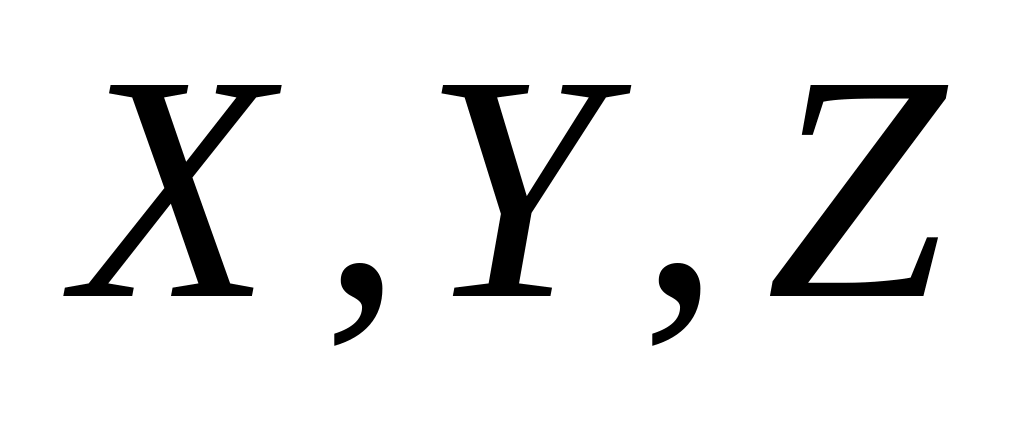– независимые случайные величины,
принимающие с вероятностью
значения 0 и 1. Верно ли, что
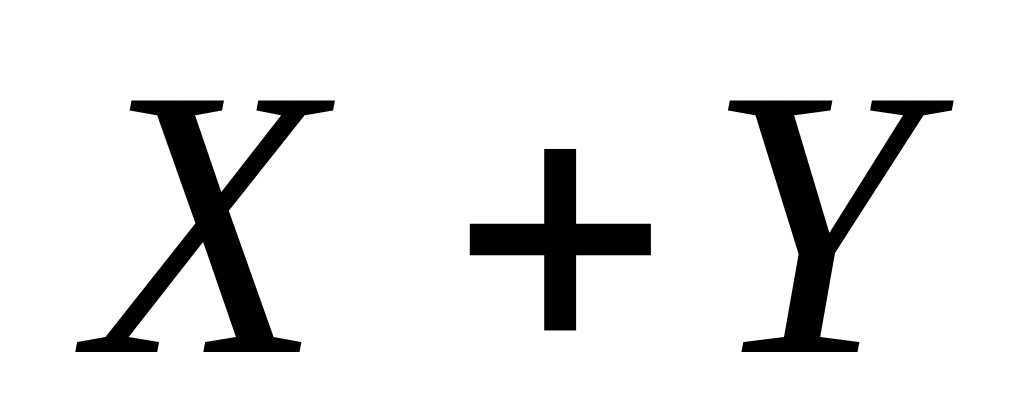и
–
независимые случайные величины?
Ответ обоснуйте.
● Математическое ожидание и дисперсия дискретной случайной величины
Дайте определение математического ожидания дискретной случайной величины. Поясните его смысл на примере случайной величины с двумя возможными значениями, исходя из статистического определения вероятности.
Перечислите основные свойства математического ожидания дискретной случайной величины. Объясните, что понимается под суммой и произведением случайных величин?
Приведите (с обоснованием) пример дискретного распределения вероятностей, для которого не существует математическое ожидание.
Может ли математическое ожидание дискретной случайной величины, принимающей целые значения, быть числом нецелым? Ответ обоснуйте.
Пусть – дискретная случайная величина, принимающая только неотрицательные значения и имеющая математическое ожидание
.
Докажите, что
.Докажите, что если и
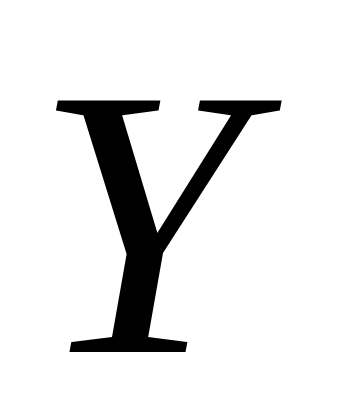– независимые дискретные случайные
величины, принимающие конечное
множество значений, то
.
Докажите, что если и – дискретные случайные величины, принимающие конечное множество значений, то
.
Как определяется и что характеризует дисперсия дискретной случайной величины ? Перечислите основные свойства дисперсии.
Докажите, что если – дискретная случайная величина, то
.
Пусть – дискретная случайная величина. Может ли выполняться неравенство
?
Ответ обоснуйте.
Докажите, что если и – независимые случайные величины, то
.Пусть – дискретная случайная величина, распределенная по биномиальному закону с параметрами и . Докажите, что
.
Докажите, что для биномиальной случайной величины с вероятностью успеха в каждом из независимых испытаний выполняется равенство
.
Пусть – дискретная случайная величина, распределенная по закону Пуассона с параметром
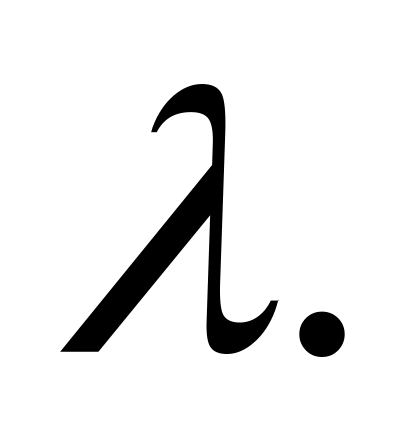Докажите, что
.Пусть – дискретная случайная величина, распределенная по геометрическому закону с параметром
Докажите, что
Пусть – дискретная случайная величина, распределенная по геометрическому закону с параметром Докажите, что
● Ковариация и коэффициент корреляции
Как определяется ковариация Cov
случайных величин
и
?
Докажите, что
Cov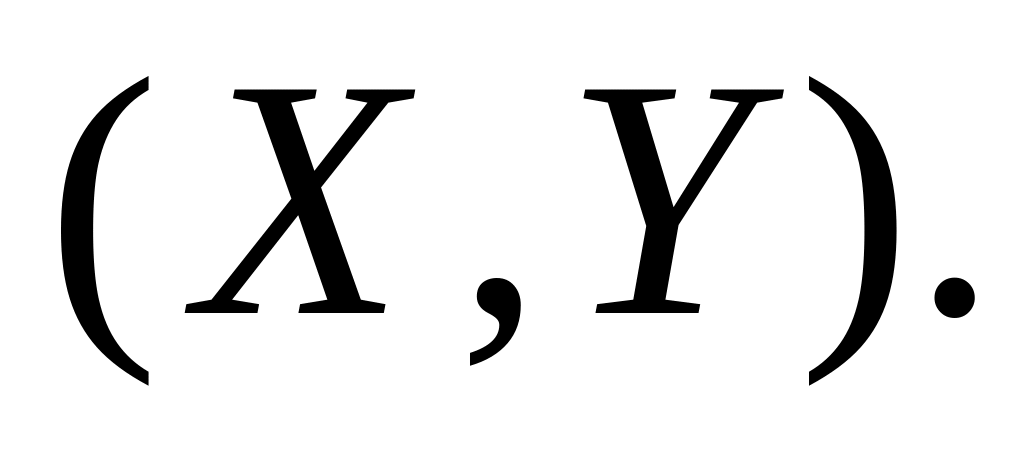
Сформулируйте основные свойства ковариации Cov случайных величин и . Докажите, что Cov
.Как определяется коэффициент корреляции
случайных величин
и
?
Каковы основные свойства коэффициента
корреляции? Что можно сказать о
и
,
если
Докажите, что коэффициент корреляции
случайных величин
и
удовлетворяет условию
.
Что можно сказать о
и
,
если
?
Если
Чему равен и Cov при условии независимости случайных величин
?
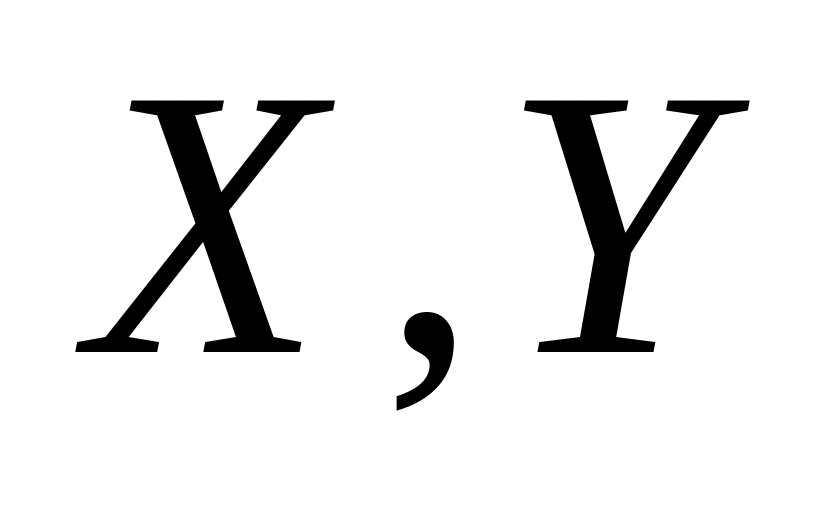Что можно сказать о
,
если
,
где
и
– некоторые числа
?
Ответ обоснуйте.