2.3. Область визначення та множина значень функції, заданої

аналітично

Означення 5. Областю визначення функції називається сукупність усіх тих значень аргументу х, для яких значення у, обчислені за формулою, будуть дійсними числами.

Якщо спеціально не обумовлено, то під областю визначення функції розуміють область допустимих значень незалежної змінної х, при яких функція y=f(x) має зміст.

Наприклад, областю визначення функції є напівінтервал , оскільки х-10  0; якщо ж змінна х позначає час, то природно розглядати додаткову умову х  0 і тоді областю визначення функції буде відрізок X=[0, 10].

Якщо , то у приймає дійсні значення лише при х² - 9  0  х²  9 х  3, тобто х  -3 та х  3.

Таким чином, областю визначення цієї функції буде наступне об’єднання множин X = (-; -3)  (3; +).

Означення 6. Множиною значень функції y=f(x) називається сукупність усіх значень у, коли х змінюється в області визначення функції.

Так, для функції множиною значень буде напівінтервал .

2.4. Деякі властивості функцій

Функція є змінною величиною, тому вона може бути зростаючою або спадною, обмеженою (зверху або знизу, або зверху та знизу). Крім цих властивостей часто використовують властивості парності та періодичності.

Монотонність. Функція y=f(x) називається зростаючою (спадною) на проміжку Х, якщо більшому значенню аргументу із цього проміжку відповідає більше (менше) значення функції.

Нехай і . Тоді функція зростає на проміжку Х, якщо , і спадає, якщо (рис. 1). Якщо ж для і випливає нерівність ( ), то функцію y=f(x) називають неспадною (незростаючою) на проміжку Х.

Зростаючі (спадні) і неспадні (незростаючі) функції називають монотонними.

y=f(x)

Y

Y

f(x₂)

y=f(x)

f(x₁)

f(x₁)

f(x₂)

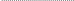
О

a

b

x₁

x₂

X

О

a

b

x₁

x₂

X

Рис. 1

Обмеженість. Функція y=f(x) називається обмеженою на проміжку Х, якщо існує таке додатне число М > 0, що  f(x)   М для будь-якого х  Х. В протилежному випадку функція називається необмеженою.

Наприклад, функція y=sin x обмежена на всій числовій осі, оскільки

 sin x   1 для будь-якого х  R.

Парність і непарність. Функція y=f(x) називається парною, якщо для будь-якого значення х з області визначення f(-x)= f(x) і непарною, якщо . В іншому випадку функція y=f(x) називається функцією загального вигляду.

Наприклад, функція y= x² є парною ( так як f(-x)= (-х)² = x² і f(-x)= f(x)), а функція y= x³ є непарною ( так як f(-x)= (-х)³ = -x³ і f(-x)= -f(x)).

Разом із тим функція y= x²+ x³ є функцією загального вигляду, оскільки f(-x)= (- x)²+ (-x)³ = x² - x³ і f(-x) f(x) і f(-x) - f(x).

Відмітимо, що графіки парних функцій симетричні відносно осі ординат, а непарних функцій – симетричні відносно початку координат (рис. 2).

Рис. 2

Періодичність. Функція y=f(x) називається періодичною з періодом Т0, якщо для будь-якого числа х з області визначення функції f(x+Т) =f(x).

Найменше додатне число Т, що задовольняє цю рівність, називається періодом функції. Наприклад, для функції маємо період Т=2, оскільки для будь-якого х, , аналогічно для функції періодом є число Т= .

Приклад. Знайти найменший додатній період функції , де k, b ­– числа.

Розв’язання. Нехай Т – шуканий період. За означенням періодичної функції маємо

,

або

.

Ввівши позначення і підставивши значення z замість в останню рівність, дістанемо .

Оскільки найменшим додатним періодом синуса є , то , звідки .

Користуючись одержаним результатом, можна стверджувати, що періодом функції є число , а функції – число .