Розділ 3. ГРАНИЦЯ ЗМІННОЇ ТА ФУНКЦІЇ

Границя числової послідовності. Основні теореми про границі числових послідовностей. Число е. Натуральні логарифми. Границя функції на нескінченності і в точці. Однобічні границі. Основні теореми про границі функції. Нескінченно малі та нескінченно великі величини. Розкриття деяких невизначеностей. Дві важливі границі. Задача про неперервне нарахування відсотків. Неперервність функції. Класифікація точок розриву функції. Неперервність функції в точці і на відрізку. Властивості неперервних функцій.

3.1. Границя числової послідовності

Означення 1. Якщо за певним законом кожному натуральному числу n поставлено у відповідність цілком визначене число , то кажуть, що задана числова послідовність

Іншими словами, числова послідовність – це функція натурального аргументу: .

Розглянемо, наприклад, послідовність . Зобразимо задану послідовність точками на числовій прямій (рис. 1).

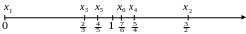
Рис. 1.

Легко бачити, що з ростом n, члени послідовності як завгодно близько наближаються до 1. При цьому стає все меншим і меншим, тобто з ростом n буде менший за будь-яке, як завгодно мале додатне число.

Означення 2. Число a називається границею числової послідовності , якщо для будь-якого, як завгодно малого додатного числа , знайдеться такий номер , що для всіх членів послідовності з номерами має місце нерівність .

Якщо числова послідовність має границю а, то вона називається збіжною (до числа а) і ми пишемо

. (1)

Зауважимо, що інколи замість (1) пишуть просто при .

За допомогою логічних символів (кванторів) (для всіх, для всякого), (існує, знайдеться) і (слідує) означення границі числової послідовності можна записати так:

.

Приклад 1. Виходячи з означення границі числової послідовності довести, що .

Дійсно, згідно означення границі

.

З останньої нерівності випливає, що . Звідки . Тоді за N можна взяти цілу частину , тобто . Наприклад, при . Це означає, що задана послідовність має границю число 1.

Приклад 2. Нехай . Покажемо, що . Взявши довільне , розглянемо нерівність і вияснимо, для яких n вона справедлива. Маємо:

Таким чином, взявши за N найближче до справа додатне ціле число, будемо мати, що справедлива для всіх N>n, що означає справедливість рівності .

3.2. Основні положення про границі числових послідовностей

1⁰. Збіжна послідовність має тільки одну границю.

2⁰. Збіжна послідовність завжди обмежена.

3⁰. Якщо члени збіжної послідовності задовольняють нерівність , то і .

4⁰. Якщо члени двох збіжних послідовностей і задовольняють нерівностям , то і .

Означення 3. Послідовність називається:

зростаючою, якщо для всіх n,

неспадною, якщо для всіх n,

спадною, якщо для всіх n,

незростаючою, якщо для всіх n.

Усі такі послідовності називаються монотонними. Справедливі наступні фундамен­тальні теореми, які ми приймемо без доведення.

Теорема 1 (Гур’єва або про порушника і двох конвоїрів). Якщо члени трьох послідовностей , і задовольняють нерівностям і при цьому послідовності і мають одну і ту ж границю а, то і послідовність має границю а, тобто .

Теорема 2 (достатня умова збіжності послідовності). Обмежена монотонна послідовність завжди має скінчену границю, тобто є збіжною.

Приклад 3. Довести, що послідовність має скінчену границю, тобто збігається.

Доведення. Покажемо, що ця послідовність обмежена. Для цього запишемо її загальний член у вигляді , звідки випливає, що .

Дослідимо цю послідовність на монотонність. Розглянемо часту .

Таким чином, , тобто послідовність зростаюча, а отже, за теоремою 2 вона має скінчену границю. Легко переконатись, що .