Розділ 4. Похідна і диференціал функцій однієї змінної

4.1. Похідна функції в точці Нехай функція визначена в деякому околі точки .

Означення 1. Похідною функції в точці називають границю відношення приросту функції до приросту аргументу , коли довільним чином прямує до нуля. Якщо існує границя відношення , то її позначають через: , , або . Таким чином математично похідна в точці визначається за формулою:

. (1)

Означення 2. Операцію знаходження похідної функції називають диференціюванням цієї функції. Функцію , яка має похідну в точці , на­зивають диференційованою в точці . Якщо функція має похідну в кожній точці деякого проміжку, то вона називається диференційованою на цьому проміжку.

Приклад 1. Для функції знайти похідну, користуючись означенням. Як відомо, задана функція неперервна в кожній точці інтервалу визначення .

Маємо

.

Очевидно, що

. Отже .

4.2. Деякі задачі, що приводять до поняття похідної

1. Задача про швидкість руху. Механічний зміст похідної

Нехай тіло рухається прямолінійно вздовж деякої осі із швидкістю . Починаючи з деякого часу , за час тіло пройде шлях . Тоді середня швидкість руху тіла буде .

Коли проміжок часу зменшується , тоді наближається до швидкості руху в момент , що відповідає початку проміжку .

Означення 3. Миттєвою швидкістю (або швидкістю в момент часу ) називають границю відношення приросту шляху до приросту часу , коли , тобто

. (2)

Таким чином робимо висновок: похідна є величиною миттєвої швидкості в момент , тіла, що рухається за законом .

2. Задача про дотичну. Геометричний зміст похідної

Нехай задана функція . Графіком цієї функції на площині буде деяка крива лінія.

Означення 4. Дотичною до кривої в точці (точки дотику) називають граничне положення січної , коли точка , рухаючись вздовж кривої, прямує до точки дотику (Рис. 1).

Точка має координати та . Тому .

Якщо , то і тому . А отже, . (3)

Тому, рівняння дотичної буде

або . (3)

Таким чином похідна дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою , тобто .

3. Задача про продуктивність праці. Економічний зміст похідної

Нехай функція виражає кількість виробленої продукції u за час t. Необхідно знайти продуктивність праці в момент часу t₀ .

Очевидно за період часу від t₀ до t₀ + t кількість виробленої продукції зміниться від значення до . Тоді середня продуктивність праці за цей відрізок часу . Продуктивність праці в момент часу t₀ можна визначити як граничне значення середньої продуктивності за період часу від t₀ до t₀ + t при t0, тобто

. (4)

Отже похідна обсягу виробленої продукції за часом є продуктивність праці в момент часу t. У цьому полягає економічний зміст похідної.

Приклад 2. Розглянемо виробничу функцію, яка зв’язує кількість виробленої продукції Q і кількість затраченої праці L (для фірми це може бути чисельність персоналу) вигляду .

Граничну продуктивність праці будемо шукати користуючись означенням похідної:

.

Підставляючи в одержану формулу значення L, легко знайти відповідні величини граничної продуктивності праці. Для прикладу візьмемо:

.

Результати обчислень наведено в таблиці

L	1	9	100	2500	22500
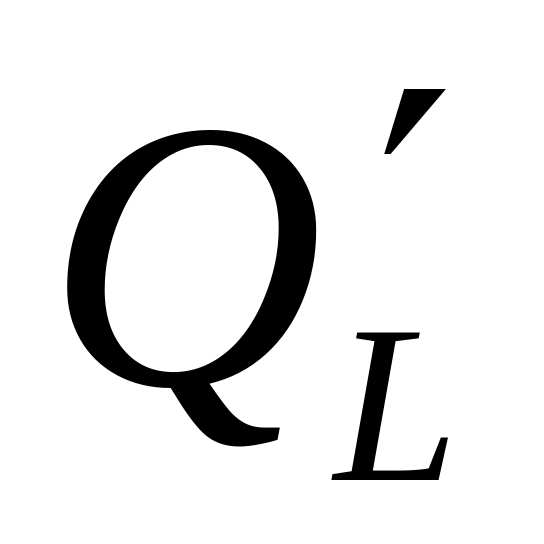
	146	46	11	-1	-3

Із наведеної таблиці видно, що гранична продуктивність праці зменшується з ростом чисельності персоналу і, починаючи з деякої кількості стає від’ємною. Це означає, що при подальшому збільшені персоналу продуктивність праці буде падати. На практиці таке часто спостерігається. Якщо для виконання певної роботи залучається багато виконавців, вони починають заважати один одному.