I,j,k : IntType;

Begin

{Обратный ход}

k:= 0;

For i:=1 to N do

begin

X[i]:= B[i]/A[i,i];

k:= k+1;

{Заполнение Form1.ProgressBar2}

Form1.ProgressBar2.Position:=Round(100*k/N);

end;

End; {Solution}

procedure Jordan(N:IntType;Var A:TMatrix; Var B:TVector; Var X:TVector);

{Реализация метода Жордана}

Var

I, j, k : IntType;

S : String;

Flag : Boolean;

begin

Form1.Memo1.Visible:= True;

Form1.Memo1.Clear;

FactorizJordan(N,A,B); {Факторизация}

SolutionJordan(N,A,B,X); {Решение}

Form1.Memo1.Lines.Add('Решение СЛАУ методом Жордана');

For i := 1 to N do

Form1.Memo1.Lines.Add(Format('X[%d] = %f', [i, X[i]]));

For i:= 1 to N do

Form1.StringGrid1.Cells[N+3, i]:= FloatToStrF(1.0*X[i],ffGeneral,3,3);

end;

1.1.6.8. Факторизация

Матица коэффициентов может быть разложена в произведение нижней треугольной и верхней треугольной матриц, т. е.

,

при условии, что и её верхние левые главные подматрицы не вырождены. Кроме того, если симметрична, то верхняя треугольная матрица является транспонированной по отношению к нижней треугольной матрице, и у обеих этих матриц на главной диагонали находятся единицы. Таким образом,

.

По очевидным причинам, это разложение часто называют тройной факторизацией. Используя данное представление, можно решить матричное уравнение системы за два шага

,

где

.

Сначала решается первое уравнение относительно , а затем второе уравнение относительно . Элементы матриц и могут быть вычислены по формулам

,

,

где сумма полагается равной нулю, если верхний предел суммирования меньше нижнего. Векторы и определяются по формулам

,

,

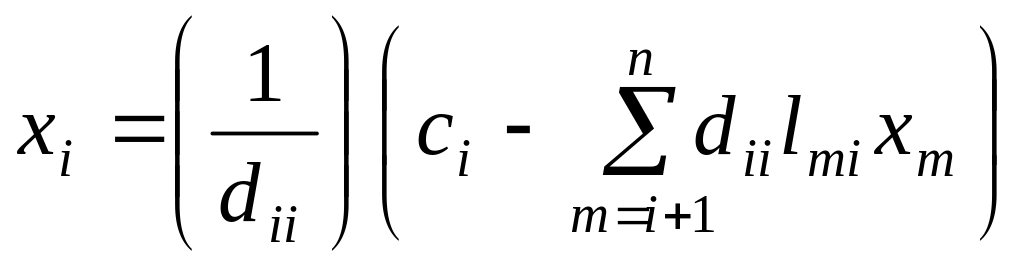где – размерность квадратной матрицы коэффициентов .

Разложение может быть выполнено весьма эффективно посредством вычисления элементов и по столбцам. Эта процедура предпочтительнее простого метода исключения Гаусса, так как она значительно более быстрая.

1.1.6.9. Метод квадратных корней (Холесского)

Вариант 1.

Если матрица - симметричная положительно определённая, то часто используемой альтернативой гауссовому исключению является разложение Холесского.

Основная идея метода квадратных корней состоит в том, что симметричная матрица системы (2) представляется в виде произведения двух транспонированных треугольных матриц

,

где L – нижнетреугольная матрица, а

Чтобы завершить решение линейной системы , нужно выполнить прямую и обратную подстановки

.

Одна из возможных реализаций разложения показана ниже. Поскольку - симметричная матрица, достаточно хранить лишь нижнюю (или верхнюю) её треугольную часть. В самом внутреннем цикле (цикл по ) модифицируются столбцы матрицы путём вычитания из них столбцов , умноженных на соответствующие числа.

Другая реализация. Выводится формула для определения элементов матрицы

После этого решение системы (1.2) сводится к решению двух треугольных систем

где - вспомогательный вектор-столбец с компонентами

1. Вычисление элементов матрицы .

2. Определение элементов вспомогательного вектора y.

3. Нахождение неизвестных xB_{i B}.

Вариант 2.

Матрица симметричная и положительно определённая может быть разложена в произведение нижней треугольной матрицы с положительными диагональными элементами на её транспонированную, а именно:

.

С другой стороны, матрица может быть разложена в произведение верхней треугольной матрицы на её транспонированную:

.

Для первого из этих разложений подстановка в выражение даёт уравнение

,

которое может быть записано в виде последовательности уравнений

Прямая подстановка, даёт матрицу , а обратная подстановка, может быть определена явно через элементы матрицы с помощью следующих соотношений:

,

,

,

где сумма полагается равной нулю, если верхний предел суммирования меньше нижнего.

Очевидно, что для этого алгоритма при вычислении элемента требуются лишь элемент и элементы матрицы , указанные на рис.1,а двумя жирными линиями. Если элементы в треугольнике находятся в оперативной памяти, а элементы заменяются вычисленными элементами (указанных жирными линиями в матрице ) находятся в выделенных линиями частях матрицы . После определения каждый новый элемент записывается вместо соответствующего элемента .

Таким образом, вычисление элементов осуществляется вдоль линии BC вплоть до нижней границы ленты. После этого необходимо переслать одну строку во внешнюю память из активного треугольника, а новый столбец – в оперативную память, как это схематично показано на рис.1.2,б.

Рис. 1.2: Разложение Холесского.

а – рабочие области; б – изменение активной области.

Пример 1.10

procedure Cholessky(N:IntType; A:TMatrix; B:TVector; Var X:TVector);

{Реализация метода Холесского}

Var