1.1.3. Собственные значения и собственные векторы матриц

Любой вектор , , для которого , где - некоторое число, называется собственным вектором , а - собственным значением матрицы .

Уравнение эквивалентно .

Многочлен - характеристический многочлен матрицы , - характеристическое уравнение матрицы , - его решения – собственные значения матрицы .

Пример 1.1

Пусть

Пример 1.2

Пусть

Действительных собственных чисел нет.

Пример 1.3

Пусть

На выбор метода большое влияние оказывает также порядок системы, сложность вычислительной схемы, допустимая погрешность, объём вычислений, быстродействие метода.

В силу этого нет, и не может быть одного универсального метода, который бы во всех случаях являлся наилучшим.

1.1.4. Векторные нормы

Норма вектора – это число, изменяющее общую величину элементов вектора. Она обозначается символом . Задать норму можно многими способами. Теоретически всякая функция, удовлетворяющая приводимым ниже четырём условиям, приемлема в качестве нормы. Большинство теорем, в формулировках которых участвуют нормы, верны независимо от того, какие именно это нормы. Поэтому их формулировки можно читать, заменяя для большего удобства символ нормы символом длины вектора. Однако нормы используются также при вычислениях, и здесь выбор конкретной нормы имеет большое значение. Наиболее употребительная векторная норма – это евклидова длина, или 2-норма

.

Она имеет то достоинство, что соответствует нашему интуитивному представлению о расстоянии. Однако применение 2-нормы к исследованию линейных уравнений ведёт к избыточным вычислениям. Поэтому часто для упрощения вычислений пользуются следующей формулой:

.

Она называется 1-нормой.

Третьей часто используемой нормой является max-норма, или -норма

.

Возвращаясь к определению нормы, заметим, что нормой называется любая функция, удовлетворяющая условиям

, если

для любого числа ,

.

Таким образом, норма обладает многими аналитическими свойствами евклидовой длины. Некоторые геометрические свойства последней утрачиваются, но они не столь важны.

1.1.5. Методы решения некорректных задач

Среди математических задач выделяется класс задач, решения которых неустойчивы к малым изменениям исходных данных. Они характеризуются тем, что сколь угодно малые изменения исходных данных могут приводить к произвольно большим изменениям решений. Задачи подобного типа, по существу, являются плохо поставленными. Они принадлежат к классу некорректно поставленных задач.

Если исходные данные известны приближённо, то упомянутая неустойчивость приводит к практической неединственности решения в рамках заданной точности и к большим трудностям в выяснении смысла получаемого приближённого решения. В силу этих особенностей долгое время считалось, что некорректно поставленные задачи не могут иметь практического значения.

Однако можно указать некорректно поставленные задачи, относящиеся как к классическим разделам математики, так и к различным классам практически важных прикладных задач.

Среди таких задач - решение интегрального уравнения Фредгольма первого рода с ядром , к которому приводится ряд физических задач,

где - искомая функция из пространства , - заданная функция из пространства .

В операторной форме это уравнение будет выглядеть как

,

где - матрица с элементами - искомый вектор с координатами , - известный вектор с координатами , , .

В практических задачах часто правая часть и элементы матрицы , т.е. коэффициенты системы уравнений, известны приближённо. В этих случаях вместо исходной системы мы имеем дело с некоторой другой системой такой, что , , где смысл норм обычно определяется характером задачи. (Так для евклидовой нормы )

В этих случаях о точной системе , решение которой надо определить, нам известно лишь то, что для матрицы и её правой части выполняются неравенства и . Но систем с такими исходными данными бесконечно много, и в рамках известного нам уровня погрешности они неразличимы. Поскольку вместо точной системы мы имеем дело с приближённой системой , то речь может идти лишь о нахождении приближённого решения. Но приближённая система может быть неразрешимой.

А. Н. Тихоновым предложено заменить точное решение системы псевдорешением с минимальной нормой :

.

Псевдорешение наименьшей нормы, так называемое нормальное псевдорешение, всегда существует и единственно. Устойчивый алгоритм нахождения нормального псевдорешения реализуется при решении системы уравнений

,

где - малый параметр (коэффициент регуляризации);

- единичная матрица;

- транспонированная матрица .

Решение последней системы уравнений является приближённым к исходному значению , причём .

Если коэффициент регуляризации слишком мал, то система уравнений переходит в плохо обусловленную. Если же он велик, то регуляризованная система будет хорошо обусловленной благодаря присутствию в левой части хорошо обусловленной матрицы , но сама система при большом сильно отличается от исходной и регуляризованное решение не будет близким к исходному решению. Поэтому слишком малое или слишком большое непригодны. Оптимальным будет наименьшее значение , при котором обусловленность системы ещё удовлетворительна.

Для фактического нахождения оптимума вычисляют невязку и сравнивают её по норме с известной погрешностью правой части и с влиянием погрешности коэффициентов матрицы . Проводят серию расчётов с различными коэффициентами ; оптимальным считают тот, в котором .

Обычно всегда удовлетворяет неравенству

,

где - число обусловленности матрицы .Чаще всего .

Если в коэффициенты матрицы и значения в правой части системы имеют различные порядки (например, коэффициенты матрицы имеют порядок , а значения в правой части системы - ), то вначале необходимо выполнить так называемое «центрирование».

«Центрирование» по столбцам матрицы и вектора правой части:

- текущий номер столбца, - порядок системы.

«Центрированная» матрица и вектор правой части системы уравнений имеют вид

;

Решение восстанавливается по формуле:

.

Пример 1.4 постановки некорректно поставленной задачи.

Связь между распределением вектора намагниченности постоянного магнита и напряжённостью созданного им поля выражается уравнением магнитостатики:

,

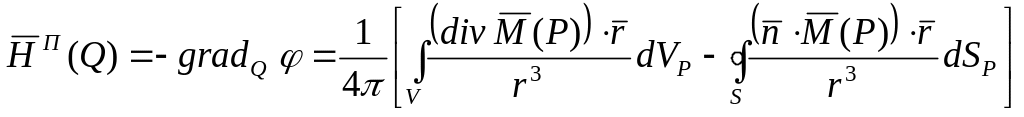где и - соответственно, объём, и поверхность магнита;

- модуль радиус-вектора, соединяющего точку наблюдения с переменной точкой в области магнита;

- нормаль к поверхности;

.

Это уравнение с помощью различных рассуждений и преобразований может быть сведено к интегралу по объёму постоянного магнита

или к интегрированию нормальной составляющей намагниченности элемента

,

где - площадь -й грани элемента магнита;

- число граней (общее число элементарных площадок), в пределах которых .

И в том, и в другом случае после дискретизации области постоянного магнита получим систему уравнений

,

где - вектор, составленный из элементов массива данных измерений напряжённости внешнего магнитного поля, создаваемого постоянным магнитом;

- вектор, образованный искомыми компонентами намагниченности в элементарных объёмах;

- матрица коэффициентов.

По своей постановке данная задача является некорректной.