1.1. Численные методы решения систем линейных алгебраических уравнений (слау)

1.1.1. Классификация методов

Для решения СЛАУ, записанных в развёрнутом виде:

(1.1)

или в матричном виде

(1.2)

применяются различные методы, которые можно разделить на три группы:

1. точные;

2. итерационные;

3. статистических испытаний.

Точные методы позволяют в результате конечного, заранее известного числа арифметических операций получить искомое решение. Они называются точными потому, что существует принципиальная возможность получить с их помощью точный результат. Однако в практике вычислений они не дают точного результата, так как приходится учитывать влияние исходных погрешностей и ошибок округления.

Для итерационных методов характерно то, что,

во-первых, они требуют начальных приближенных значений неизвестных,

во-вторых, решение ищется по итерационной схеме в виде последовательности постепенно улучшающихся приближений, число которых заранее может быть неизвестным, и,

в-третьих, для получения искомого решения необходимо, чтобы итерационный процесс был сходящимся. Итерационные методы позволяют получить приближенное решение с практически любой степенью точности, хотя точное решение за конечное число шагов в этом случае получить невозможно; точный результат является пределом бесконечной последовательности приближений.

В вычислительной практике процесс итерации обычно продолжается до тех пор, пока два последовательных приближения не совпадут с нужным числом знаков.

Методы статистических испытаний (методы Монте-Карло) носят вероятностный характер. Они предполагают использование случайных величин, математическое ожидание которых равняется искомому решению

Многие методы решения системы (1.2) связаны с обращением матриц, так как значения неизвестных удовлетворяют матричному равенству

, (1.3)

где - матрица, обратная матрице . При этом предполагается, что матрица коэффициентов является невырожденной.

1.1.2. Обусловленность системы уравнений

Выбор метода зависит от многих обстоятельств. При выборе метода большую роль играет степень обусловленности системы. Система считается хорошо обусловленной, если небольшие изменения в коэффициентах и свободных членах незначительно сказываются на её решении. Это условие равносильно тому, что при малых изменениях матрицы незначительно изменяются и элементы обратной матрицы . Если же малые изменения в матрице приводят к существенным изменениям в обратной матрице , то система является плохо обусловленной.

Иногда обусловленность системы оценивают по величине определителя . Однако такая оценка не может вполне характеризовать степень обусловленности системы. Более надёжной оценкой является величина элементов обратной матрицы . Если эти элементы велики, то система плохо обусловлена. Другими критериями обусловленности являются так называемые числа обусловленности, среди которых

где - собственные значения матрицы , - евклидова норма матрицы .

Число обусловленности матрицы можно определить следующим образом:

К понятию числа обусловленности

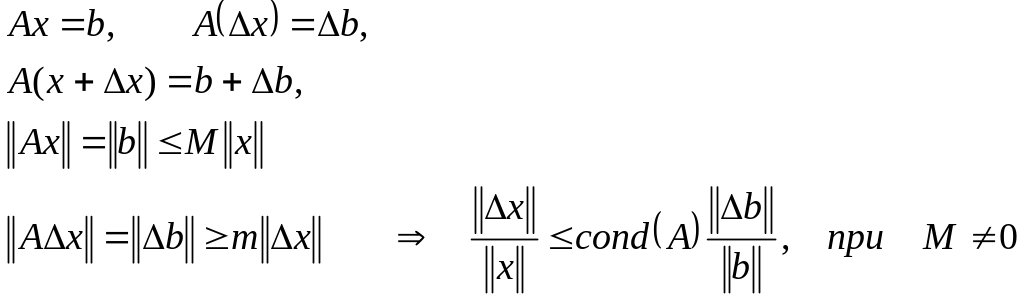
Полученное неравенство показывает, что число обусловленности выполняет роль коэффициента увеличения относительной ошибки. Изменения правой части могут повлечь за собой изменения в решении, большие в раз. Это справедливо и в отношении изменений в коэффициентах матрицы.

Число обусловленности является также мерой близости к вырожденности, если оно велико, то матрица близка к вырожденной.