1.1.6.4. Матрично-векторные формы - разложения

В основе простейшего из способов организации вычислений, основанных на операциях с подматрицами, лежит метод окаймления.

Существует два естественных способа реализации окаймления в -разложении. В первом варианте треугольные системы решаются с помощью столбцового алгоритма; во втором случае системы решаются с помощью алгоритма скалярных произведений

Столбцовый алгоритм	Алгоритм скалярных произведений

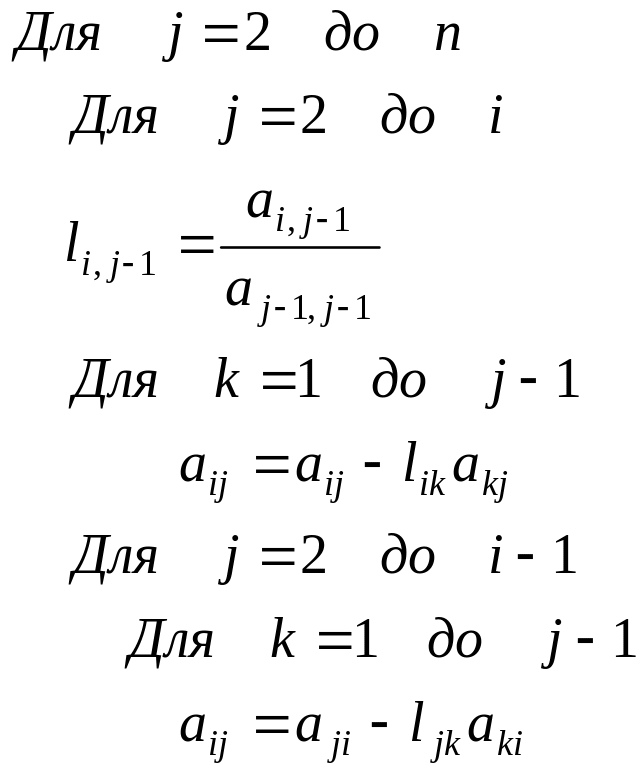
1.1.6.5. Алгоритм Донгарры-Айзенштата.

Данный алгоритм имеет то преимущество, что его основной операцией является матрично-векторное умножение.

Основной операцией является в этом случае умножение вектора на прямоугольную матрицу. Такие умножения реализуются посредством скалярных произведений или линейных комбинаций.

Алгоритм -разложения Донгарры-Айзенштата (линейных комбинаций)	Алгоритм -разложения Донгарры-Айзенштата (скалярных произведений)

Пример 1.7

Procedure LU(n : Integer; Var a:TMatrix);

Var I,j,k,s : Integer;

Begin

For j:= 1 to n do

begin

For i:= j+1 to n do

For k:= 1 to j-1 do

a[i,j]:= a[i,j] - a[i,k]*a[k,j];

For i:= j to n do

For k:= 1 to j-1 do

a[j,i]:= a[j,i] - a[j,k]*a[k,i];

For s:= j+1 to n do

a[s,j]:= a[s,j]/a[j,j];

end;

End; //LU

Procedure LU_O(a:TMatrix; n: Integer; Var b,x:Array of RealType);

Var I,j,k : Integer;

Begin

For i:= 1 to n do

For j:= 1 to i-1 do b[i]:= b[i]- a[i,j]*b[j];

b[n]:= b[n]/a[n,n];

For i:= n-1 downto 1 do

begin

For j:= i+1 to n do b[i]:= b[i]-a[i,j]*b[j];

b[i]:=b[i]/a[i,I];

end;

For j:= 1 to n do x[j]:= b[j];

End;//LU_O

1.1.6.6. Метод вращения

Метод вращения (метод Гивенса) является разновидностью метода Гаусса, обладающей повышенной устойчивостью к «провалам» промежуточных вычислений. Этот метод обеспечивает приведение исходной системы (1.2) к системе правой треугольной матрицы.

Матрицы вращения позволяют реализовать упорядоченное исключение переменных.

Построим ортогональную матрицу вращения так, чтобы при левом умножении обратной к ней на матрицу она обращала в ноль элемент , ( исключение переменной из второго уравнения) затем матрицу для обращения в ноль и так далее, пока не будут обращены в ноль поддиагональные элементы первого столбца матрицы :

Выполним подобную последовательность операций для всех столбцов матрицы . Получим факторизацию, на которой основан метод вращения

,

где - последовательность матриц вращения, элементы и которых определяются по формулам

Схема выполнения операции выглядит следующим образом:

Очевидно, что в результате обратится в ноль элемент а_ik.

Если необходимо решить одну систему уравнений с одной правой частью, то можно использовать следующий алгоритм решения:

Алгоритм 1.

1. Для выполнить пп. 2, 3, 4, 5.

2. Для выполнить пп. 3, 4, 5.

3. Вычислить элементы и матрицы вращения

4. Умножить матрицу слева на для чего

   1. Положить .

   2. Для выполнить

.

5. Умножить матрицу на вектор правых частей для чего выполнить

6. Решить полученную систему уравнений в верхней треугольной форме методом обратной подстановки.

7. Конец алгоритма. Матрица содержит в верхнем треугольнике матрицу , вектор - пересчитан.

Каждый шаг исключения переменной методом вращений из очередного k-го столбца системы уравнений состоит из нескольких малых шагов, на каждом из которых необходимо строить матрицу .

Следует обратить внимание на то, что в отличии от метода Гаусса пересчету на каждом малом шаге подлежат также и элементы ведущей строки B _Bс индексами столбцов .

В силу ортогональности матриц вращения метод является численно более устойчивым, чем метод Гаусса, однако требует в три раза большего количества операций, причем операций вызывают функции извлечения квадратного корня. Оценка общего числа необходимых операций приближенно равна .

Для решения систем с различными правыми частями и одинаковой матрицей факторизацию выполняют один раз, при этом элементы матриц вращения запоминают на месте обращаемых в ноль элементов матрицы . При последующих расчетах элементы могут быть рассчитаны по формуле , если они не сохранены в специальных массивах данных. При решении нескольких систем с одной матрицей коэффициентов при неизвестных: но с различными правыми частями общий объем вычислений сокращается.

Алгоритм 2.

1. Вводим и .

2. Вычисляем и , причём если

, то и . Проводим преобразования системы по формулам где

и - левые части, а и - правые части го и го уравнений соответственно.

После шагов приходим, к системе с верхней треугольной матрицей.

3. Осуществляем обратный ход:

где

Пример 1.8.

Procedure GivensFac(N:IntType; Var A:Matrix; Var B:Vector);

{Метод Гивенса. Факторизация}

Var