I, j, k : IntType;

U : TMatrix;

Y : TVector;

H : RealType;

S : String;

begin

Form1.Memo1.Visible:= True;

Form1.Memo1.Clear;

For i := 1 to N do

For j := 1 to N do

U[i,j] := 0;

{Самопреобразоваие и получение верхней треугольной матрицы }

For k:=1 to N do

begin

U[k,k]:=Sqrt(A[k,k]);

For j:= k+1 to N do

begin

U[k,j]:=A[k,j]/U[k,k];

end;

For i:=k+1 to N do

For j:= k+1 to N do

begin

A[i,j]:=A[i,j]-U[k,i]*U[k,j];

end;

{Заполнение Form1.ProgressBar2}

Form1.ProgressBar2.Position:=Round(100*k/N);

end;

Form1.Memo1.Lines.Add('Матрица U=');

{Вывод в меню марицы U}

For i := 1 to N do

begin

S := '';

For j := 1 to N do

begin

S := S+ Format('%f'#9, [U[i,j]]);

end;

Form1.Memo1.Lines.Add(S)

end;

{---------------------------------------------}

{ Пояснения к методу Холесского

A*X=B

A=Ut*U

Ut*U*X=B

1) Ut*Y=B

2) U*X=Y

U[i,j] = Ut[j,i];

}

{Решаем уравнение Ut*Y=B}

For i := 1 to N do

begin

H := 0;

For j := 1 to i-1 do

begin

H := H + U[j,i]*Y[j];

end;

Y[i] := (B[i] - H) / U[i, i];

Form1.Memo1.Lines.Add(Format('Y[%d] = %f', [i, Y[i]]));

Form1.ProgressBar2.Position:=Round(100*i/N);

end;

{Решаем уравнение U*X=Y}

For i := N downto 1 do

begin

H := 0;

For j := i+1 to N do

begin

H := H + U[i,j]*X[j];

end;

X[i] := (Y[i] - H) / U[i, i];

Form1.StringGrid1.Cells[N+2, i] := FloatToStr(X[i]);

Form1.ProgressBar2.Position:=Round(100/N*((N+1)-i));

end;

end;

1.1.6.10. Итерационное уточнение

При решении линейных алгебраических систем уравнений большой размерности накапливаются ошибки округления, полученное решение может неприемлемо отличаться от точного решения. В этом случае может быть применено итерационное уточнение, под которым понимают следующий процесс:

1. Решить исходную систему уравнений .

2. Вычислить вектор невязок . Если все 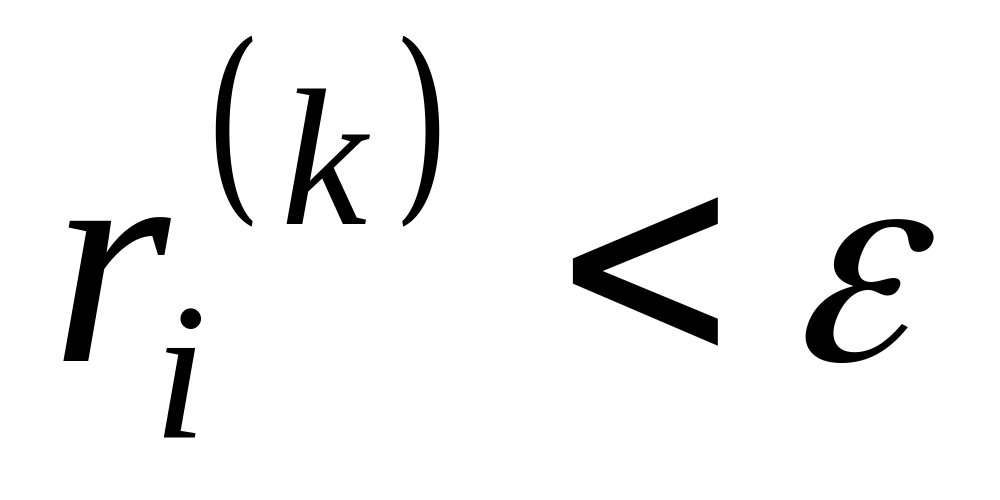, где - желаемая точность, то расчет закончен и есть решение, иначе выполнить пп. 3, 4, 5.

3. Решить систему уравнений относительно - вектора итерационного уточнения.

4. Вычислить уточненное решение

5. Повторить пп. 2, 3, 4, 5.

6. Конец алгоритма.

Приведенный алгоритм вытекает из следующих соотношений:

,

т.к. имеем: .

Следует иметь ввиду, что итерационное уточнение сходится, если для матрицы максимальное собственное число , при значениях сходимость может быть очень медленной, а при процесс скорее всего расходится.

Недостатком метода итерационного уточнения является необходимость сохранения исходной матрицы для вычисления вектора невязок, а также увеличение количества операций. Однако, в ряде случаев для обеспечения точности расчета итерационное уточнение может быть полезным.

1.1.6.11. Особенности решения слау для ленточных симметричных и несимметричных матриц

Использование многих численных методов решения инженерных и физических задач приводит к системе линейных алгебраических уравнений, большое число коэффициентов которой равно нулю. Для ленточной матрицы характерно, что большинство ненулевых коэффициентов и некоторые нулевые находятся между двумя линиями, параллельными главной диагонали. Расстояние между главной диагональю и этими линиями называется шириной полосы матрицы. Все коэффициенты вне этой полосы равны нулю, и они не должны сохраняться в машинной памяти.

Определение. Ленточная матрица – это матрица, все ненулевые элементы которой находятся вблизи главной диагонали, точнее, для всех , что , где . Шириной ленты называется число ; ненулевые элементы размещаются на диагоналях.

Примеры матриц

Ленточная симметричная матрица [9x9]. Ширина полосы = 5											Ленточная несимметричная матрица [9x9]. Ширина полосы = 5
Коэффициенты матрицы											Коэффициенты матрицы
9	1	2	3	4	0	0	0	0	1		9	1	2	3	4	0	0	0	0	1
1	9	1	2	3	4	0	0	0	2		1	9	1	2	3	4	0	0	0	2
2	1	9	1	2	3	4	0	0	3		1	1	9	1	2	3	4	0	0	3
3	2	1	9	1	2	3	4	0	4		1	1	1	9	1	2	3	4	0	4
4	3	2	1	9	1	2	3	4	5		1	1	1	1	9	1	2	3	4	5
0	4	3	2	1	9	1	2	3	6		0	1	1	1	1	9	1	2	3	6
0	0	4	3	2	1	9	1	2	7		0	0	1	1	1	1	9	1	2	7
0	0	0	4	3	2	1	9	1	8		0	0	0	1	1	1	1	9	1	8
0	0	0	0	4	3	2	1	9	9		0	0	0	0	1	1	1	1	9	9

^{Возможные способы хранения ленточной симметричной матрицы}

Ленточная симметричная матрица [9x9] Способ хранения – полоса [9x5] Верхняя треугольная матрица								Ленточная симметричная матрица [9x9] Способ хранения – полоса [9x5] Нижняя треугольная матрица
Размерность			Ширина полосы = 5					Размерность			Ширина полосы = 5
Коэффициенты матрицы								Коэффициенты матрицы
9	1	2		3	4	1		0	0	0		0	9	1
9	1	2		3	4	2		0	0	0		1	9	2
9	1	2		3	4	3		0	0	2		1	9	3
9	1	2		3	4	4		0	3	2		1	9	4
9	1	2		3	4	5		4	3	2		1	9	5
9	1	2		3	0	6		4	3	2		1	9	6
9	1	2		0	0	7		4	3	2		1	9	7
9	1	0		0	0	8		4	3	2		1	9	8
9	0	0		0	0	9		4	3	2		1	9	9

^{Рассмотрим симметричную ленточную матрицу и применительно к ней классический метод Гаусса.}

^{Пример 1.11 (для первого способа хранения данных).}

^{program GAUSSLe;}

^{{Решение СЛАУ классическим методом Гаусса }}

^{{ЛЕНТОЧНАЯ МАТРИЦА, хранится в виде прямоугольника}}

^{{от главной диагонали до ширины полосы ленты - C}}

^{{Прямой ход исключения переменных}}

^{For k:= 1 to N-1 do}

^begin

^{Imin:= k+1;}

^{Imax:= k+C-1;}

^{If Imax > N Then Imax:= N;}

^{Jmax:= C;}

^{If N-k+1 < C Then Jmax:= N-k+1;}

^{ND:= 0;}

^{For i:= Imin to Imax do}

^begin

^{Jmax:= Jmax-1;}

^{ND:= ND+1;}

^{NL:= ND+1;}

^{For j:= 1 to Jmax do}

^begin

^{NK:= ND+j;}

^{a[i,j]:= a[i,j] - a[k,NL]/a[k,1]*a[k,NK];}

^end;

^{b[i]:= b[i] - a[k,NL]/a[k,1]*b[k];}

^end;

^end;

^{{Обратный ход: последовательное нахождение корней }}

^{x[N]:= b[N]/a[N,1];}

^{For i:= N-1 downto 1 do}

^begin

^{Jmin:= 2;}

^{Jmax:= C;}

^{If i+C-1 > N Then Jmax:= N-i+1;}

^{Summa:= 0;}

^{For j:= Jmin to Jmax do Summa:= Summa + x[j+i-1]*a[i,j];}

^{x[i]:= (b[i]-Summa)/a[i,1];}

^end;