
- •Содержание
- •2. Понятие уравнения
- •2.1. Численное решение нелинейных алгебраических и транцендентных уравнений
- •2.1.1. Метод перебора
- •2.1.2. Метод дихотомии (половинного деления)
- •2.1.3. Метод отделения корней
- •2.1.4. Метод хорд
- •2.1.5. Метод касательных (метод Ньютона, метод линеаризованной итерации)
- •2.1.6. Метод секущих (комбинированный метод секущих – хорд, метод хорд - касательных)
- •2.1.7. Метод простых итераций
- •2.2. Численные методы решения систем нелинейных алгебраических уравнений (снау)
- •2.2.1. Метод последовательных приближений (простых итераций) для снау
- •2.2.2. Метод Ньютона для снау
- •2.2.2.1. Вариант 1
- •2.2.2.2. Вариант 2
- •2.2.2.3. Меры предосторожности в методе Ньютона
- •2.2.2.4. Локальное решение нелинейного уравнения
- •2.2.3. Метод Ньютона по параметру
- •2.2.4. Метод Бройдена
- •2.2.5. Метод Матвеева
- •Литература
- •Задания и примеры выполнения нахождение корня нелинейного уравнения
- •1. Постановка задачи
- •2. Методы решения задачи
- •2.1 Метод деления отpезка пополам
- •2.2 Метод простой итерации
- •2.3 Метод Ньютона
- •Методы решения системы нелинейных уравнений
- •Постановка задачи
- •2. Методы решения системы нелинейных уравнений
- •2.1.Метод простой итерации
- •2.2. Метод Ньютона
Лекции
«ОСНОВНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ,
ПРИМЕНЯЕМЫЕ В ЭЛЕКТРОТЕХНИЧЕСКИХ ЗАДАЧАХ»
(Часть II: Решение СНАУ)
Новочеркасск 2012
Содержание
СОДЕРЖАНИЕ 3
2. ПОНЯТИЕ УРАВНЕНИЯ 4
2.1. ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ И ТРАНЦЕНДЕНТНЫХ УРАВНЕНИЙ 4
2.1.1. Метод перебора 4
2.1.2. Метод дихотомии (половинного деления) 5
2.1.3. Метод отделения корней 7
2.1.4. Метод хорд 8
2.1.5. Метод касательных 9
(метод Ньютона, метод линеаризованной итерации) 9
2.1.6. Метод секущих 13
(комбинированный метод секущих – хорд, метод хорд - касательных) 13
2.1.7. Метод простых итераций 14
2.2. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СНАУ) 16
2.2.1. Метод последовательных приближений (простых итераций) для СНАУ 17
2.2.2. Метод Ньютона для СНАУ 17
2.2.2.1. Вариант 1 18
2.2.2.2. Вариант 2 19
2.2.2.3. Меры предосторожности в методе Ньютона 20
2.2.2.4. Локальное решение нелинейного уравнения 21
2.2.3. Метод Ньютона по параметру 22
2.2.5. Метод Матвеева 23
ЛИТЕРАТУРА 24
ЗАДАНИЯ и ПРИМЕРЫ ВЫПОЛНЕНИЯ 25
2. Понятие уравнения
Уравнением
с одним неизвестным
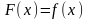 называется равенство двух функций от
одной и той же переменной величины,
верное лишь при некоторых определённых
значениях этой переменной.
называется равенство двух функций от
одной и той же переменной величины,
верное лишь при некоторых определённых
значениях этой переменной.
Уравнение
называется алгебраическим,
если каждая из входящих в него функции
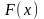 и
и
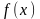 является алгебраической (рациональной
или иррациональной). Одна из этих функций
может быть постоянной величиной.
является алгебраической (рациональной
или иррациональной). Одна из этих функций
может быть постоянной величиной.
Из всякого алгебраического уравнения может быть получено уравнение в канонической форме:
 ,
,
где
коэффициенты
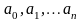 предполагаются действительными.
предполагаются действительными.
Иррациональными называются уравнения, которое содержит неизвестное под знаком радикала.
Линейным
называется уравнение вида
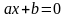 .
.
Степенные уравнения более высоких порядков называются нелинейными.
Уравнение называется трансцендентным, если хотя бы одна из функций не является алгебраической.
Примеры:

Решением
нелинейных (в частности, трансцендентных)
уравнений вида
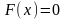 заключается в отыскании одного или всех
корней на отрезке
заключается в отыскании одного или всех
корней на отрезке
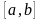 изменения
изменения
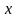 .
Обычно стараются локализовать каждый
корень в своём отрезке
.
Тогда нахождение всех корней сводится
к локализации каждого корня с последующим
сужением отрезков локализации корня
одним из описанных далее методов.
.
Обычно стараются локализовать каждый
корень в своём отрезке
.
Тогда нахождение всех корней сводится
к локализации каждого корня с последующим
сужением отрезков локализации корня
одним из описанных далее методов.
2.1. Численное решение нелинейных алгебраических и транцендентных уравнений
2.1.1. Метод перебора
При
решении нелинейного уравнения методом
перебора задаются начальное значение
аргумента
 и шаг
и шаг
 ,
который при этом определяет и точность
нахождения корней нелинейного уравнения.
Пока выполняется условие
,
который при этом определяет и точность
нахождения корней нелинейного уравнения.
Пока выполняется условие
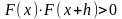 ,
аргумент
увеличивается на шаг
,
аргумент
увеличивается на шаг
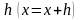 .
Если произведение
.
Если произведение
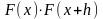 становится отрицательным, то на интервале
становится отрицательным, то на интервале
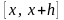 существует решение уравнения. Алгоритм
метода изображен на блок-схеме ниже.
существует решение уравнения. Алгоритм
метода изображен на блок-схеме ниже.

Рис. 1.
2.1.2. Метод дихотомии (половинного деления)
Пусть задана непрерывная функция и требуется найти все или некоторые корни уравнения.
.
Для
этого метода существенно, чтобы функция
была непрерывна и ограничена в заданном
интервале
внутри которого ищется корень.
Предполагается также, что
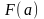 и
и
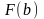 имеют разные знаки.
имеют разные знаки.
Пусть
найдены такие точки
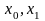 ,
что
,
что
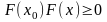 ,
т. е. на отрезке
,
т. е. на отрезке
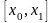 лежит не менее одного корня уравнения.
Найдем середину отрезка
лежит не менее одного корня уравнения.
Найдем середину отрезка
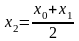 и вычислим
и вычислим
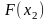 .
Из двух половин отрезка выберем ту, для
которой
.
Из двух половин отрезка выберем ту, для
которой ,
ибо один из корней лежит на этой половине.
Затем новый отрезок опять делим пополам
и выберем ту половину, на концах которой
функция имеет разные знаки, и т. д. (рис.
2).
,
ибо один из корней лежит на этой половине.
Затем новый отрезок опять делим пополам
и выберем ту половину, на концах которой
функция имеет разные знаки, и т. д. (рис.
2).
Если
требуется найти корень с точностью
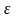 ,то
продолжаем деление пополам до тех пор,
пока длина отрезка не станет меньше
,то
продолжаем деление пополам до тех пор,
пока длина отрезка не станет меньше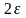 .
Тогда середина последнего отрезка даст
значение корня с требуемой точностью.
.
Тогда середина последнего отрезка даст
значение корня с требуемой точностью.
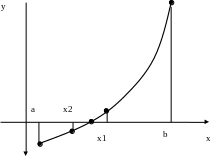
Рис. 2.
Метод
дихотомии (деления пополам) на отрезке
реализуется следующим алгоритмом (для
 )
:
)
:
Вычислить и .
Если и имеют разные знаки (
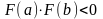 ),
то
),
тоНаходим
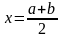 .
.Вычисляем .
Если и имеют разные знаки (
 ),
то установить
),
то установить
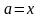 и
перейти к п. 3.
и
перейти к п. 3.Если и имеют разные знаки (
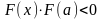 ),
то установить
),
то установить
 и
перейти к п. 3.
и
перейти к п. 3.Проверяем условие
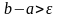 ,
если оно выполняется, идем к п.1, если
оно не выполняется, заканчиваем
вычисления и считаем что
,
если оно выполняется, идем к п.1, если
оно не выполняется, заканчиваем
вычисления и считаем что
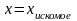 с
заданной точностью
.
с
заданной точностью
.Проверяем также условие, по которому количество итераций превышает или не превышает заданную величину.
Число
итераций при использовании этого метода:
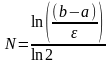 значительно, и поэтому его сходимость
медленная, однако при любой ширине
отрезка
сходимость гарантирована. Кроме того,
простота реализации метода уменьшает
число вспомогательных операций и
частично компенсирует увеличение общего
времени счета из-за медленной сходимости.
значительно, и поэтому его сходимость
медленная, однако при любой ширине
отрезка
сходимость гарантирована. Кроме того,
простота реализации метода уменьшает
число вспомогательных операций и
частично компенсирует увеличение общего
времени счета из-за медленной сходимости.
