2.1.5. Метод касательных (метод Ньютона, метод линеаризованной итерации)

Метод линеаризованной итерации, именуемый также метом Ньютона, состоит в том, что исходное уравнение заменяется последовательностью линеаризованных уравнений

каждое из которых следующее (улучшенное) приближение получается с учётом предыдущего результата

.

Итерационная формула примерно в таком же виде была получена Рафсоном в 1690 году, но за методом закрепилось название метода Ньютона, поскольку Ньютон предложил аналогичный процесс на несколько лет раньше.

Итерационный процесс продолжается до тех пор, пока разность между двумя последовательными приближениями не станет по модулю меньше заданной величины .

Для сходимости процесса линеаризованных итераций достаточно, чтобы:

• на отрезке , содержащем единственный корень уравнения, функция имела непрерывные производные и ;

• эти производные не обращались в нуль на отрезке ;

• при выбранном начальном приближении выполнялось условие .

Сходимость данного метода оценивается порядком , где - погрешность приближенного значения .

Рис. 5. Решение уравнения методом Ньютона (касательных).

В некоторых случаях метод линеаризованных итераций применяется в модифицированном виде. Первая модификация заключается в том, что на каждом шаге вычислений вместо берётся постоянная величина . В этом случае формула принимает вид

и вычисления по ней существенно упрощаются, так как величина вычисляется только один раз и в дальнейших вычислениях участвует в качестве постоянного сомножителя.

В общем случае модифицированный итерационный процесс сходится медленнее и для него ещё большее значение имеет близость начального приближения к истинному значению корня.

Вторая модификация состоит в замене исходного уравнения уравнением

в котором 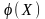подбирается так, чтобы равенство было тождественным. Корень ищется как предел последовательных приближений

;

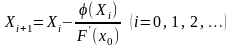
Данная итерационная формула не обеспечивает сходимости в случае, если исходное уравнение имеет двукратный корень или два очень близких корня. В этом случае более точные значения корней могут быть найдены из уравнения

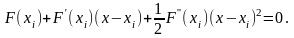
Если известно, что в окрестности имеется кратный корень, то приближенное значение может быть также улучшено по формуле

Основные достоинства метода – простота вычислительной схемы, хорошая сходимость и возможность вычисления корня с высокой точностью. Его рекомендуется применять в тех случаях, когда известно хорошее начальное приближение и требуется найти корень с высокой точностью. Особенно удобен этот метод при решении трансцендентных уравнений и нахождении комплексного корня. Перед использованием итерационной формулы необходимо поверить выполнение условий сходимости исследовать поведение первой производной и второй производной в окрестности корня. Если при этом окажется, что производная изменяется медленно, то вместо данной формулы целесообразно использовать формулу , которая существенно сокращает объём вычислений. При определении двух близких корней вычисления рекомендуется строить по формуле Если искомый корень комплексный, то в качестве начального приближения должно быть взято комплексное число.

На практике не всегда удается определить заранее кратность корня или существование двух близких корней. Поэтому оправдывает себя комбинированный способ, при котором вычисления ведутся по нескольким формулам. Алгоритм, реализующий такой способ нахождения корней, может быть следующим:

1. Вычисления по формуле при фиксированном значении (начиная с );

2. Проверка выполнения условия 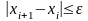. Если условие выполнено, то задача считается решенной и управление передается оператору п.7. При невыполнении указанного условия и выполнение передается следующему оператору п. 3;

3. Проверка того, достигло ли число итераций установленного предела . Если , то управление передается оператору п. 1, при выполняется следующий оператор п. 4;

4. Вычисление следующих приближений по формуле и проверка достигнутой точности вычислений. Если корень вычислен с нужной точностью, то задача считается решенной и управление может быть передано оператору п. 7. Но в окрестности этого корня имеется ещё кратный корень (или два близких корня), который может быть найден с помощью оператора п. 5. Если же нужная точность ещё не достигнута, то это, возможно, свидетельствует о том, что искомый корень является кратным или близко расположенным с другим корнем. Данное предположение проверяется с помощью оператора п. 5;

5. Вычисление следующих приближений по формуле и проверка достигнутой точности вычислений. Если нужная степень точности достигнута, то выполняется следующий оператор п. 6. При получении нужной точности задача считается решенной (при этом получаются два близких корня) и управление передается оператору п. 7;

6. Получение следующих приближений по формуле (метод хорд) ( или иному методу. Если и после этого нужная степень точности не достигается, то в окрестности искомого корня имеется более двух близких корней и для их получения следует воспользоваться другим методом;

7. Конец вычислений.

Метод Ньютона имеет квадратичную скорость сходимости.

Пример.

program Newt;

{Дана функция f(x)= tg(ax)-bx-c; a, b, c;

Решить методом Ньютона уравнение f(x)=0,c точостью до Epsi=0.0001, x0=0.01}

{Если X0 есть начальное приближение значения корня уравнения f(x)=0, то в

качестве более точного приближения берется X1= X0-f(X0)/f'(X0). Заменой X0

на X1 может быть получно следующее приближение и т. д. Процесс последовате-

льных приближений всегда сходится, если только корень Xn не кратный (т.е.

f'(Xn) <> 0) и первое придлижение взято достаточно близко}

Uses CRT;

Var

R : Integer;

x1, x0, a, b, c, Epsi, Fu, F, E : Real;

Begin

{Головная программа}

TextBackGround(Black);{Меняет цвет фона на черный, модуль Crt}

ClrScr;{Очищает экран, модуль Crt}

TextColor(LightRed);{Меняет цвет символов на светло-красный, модуль Crt}

WriteLn (' Работает программа Newt');

TextColor(Yellow);{Меняет цвет символов на желтый, модуль Crt}

WriteLn (' Введите численные значения: a, b, c, Epsi, x0:');

ReadLn(a,b,c,Epsi,x0);

R:= 0; {Флажок. Если R=0, то Cos(a*x0) <> 0.0

Если R=1, то Cos(a*x0) = 0.0}

x1:= x0;{Начальное приближение}

Repeat

If (Cos(a*x0) <> 0.0) then

begin

F:= Sin(a*x0)/Cos(a*x0) - b*x0 - c; {Значение функции}

Fu:= a/(Cos(a*x0)*Cos(a*x0)) - b; {Значение производной}

x1:= x0 - F/Fu; {Новое, уточненное приближение корня}

WriteLn(x0,x1);

E:= Abs(x1-x0); {Погрешность вычисления корня}

x0:=x1;

end

else

begin

WriteLn(' ОШИБКА! Cos(a*x0) = 0.0 ');

x0:= x1;

E:= Abs(x1-x0);

R:= 1;

end;

Until (E < Epsi);

If (R = 0) then

begin

TextColor(LightRed);{Меняет цвет символов на светло-красный, модуль Crt}

WriteLn (' **************** РЕЗУЛЬТАТ ****************');

TextColor(LightGreen);{Меняет цвет символов на светло-зеленый, модуль Crt}

WriteLn(x1);

end;

TextColor(LightGray);{Меняет цвет символов на светло-серый, модуль Crt}

WriteLn (' ДЛЯ ПРОДОЛЖЕНИЯ НАЖМИТЕ ЛЮБУЮ КЛАВИШУ!!!');

Repeat Until KeyPressed; {Ожидает нажатия любой клавиши, модуль Crt}

{Используется для задержки информации на экране}

ClrScr;{Очищает экран, модуль Crt}

{Ответ:x1}

End.{Newt}