2.1.6. Метод секущих (комбинированный метод секущих – хорд, метод хорд - касательных)

В методе секущих линейная аппроксимация функции строится с использованием двух предыдущих итераций и . Метод основан на уточнении приближённого значения корня с помощью линейной интерполяции. При этом на каждом шаге за приближённое значение корня принимается корень интерполяционного многочлена первой степени, построенного по значениям функции в точках и .

Вычисления строятся по итерационной формуле

.

Это и есть формула метода секущих.

Геометрический смысл такого изменения алгоритма Ньютона в том, что от аппроксимации функции касательной мы переходим к секущей (рис. 6).

Рис. 6. Метод секущих.

Заметим, что формула метода секущих соответствует формуле метода Ньютона, в которой используется аппроксимация

.

Использование этой аппроксимации избавляет нас от необходимости вычислять производную, но приводит к замедлению сходимости алгоритма.

Для того, чтобы начать итерационный процесс, необходимо задать два начальных приближения x ₀ и x ₁. Затем каждое новое приближение к корню получаем по формуле . Заканчиваем процесс уточнения корня при выполнении условия x _k+1 - x _k 

где – заданная абсолютная погрешность определения корня.

Метод секущих уступает методу Ньютона в скорости сходимости, однако не требует вычисления производной левой части уравнения.

По алгоритму метод секущих близок к методу хорд, однако в отличии от последнего, начальные приближения в методе секущих могут располагаться как с разных сторон от корня, так и с одной стороны; кроме того, при уточнения корня не проверяются знаки функции .

Метод секущих сходится сверхлинейно со скоростью .

Метод секущих может не сходится, во многом по тем же самым причинам, что и метод Ньютона. Например, при метод просто неопределён. Однако, многие проблема можно обойти, если включить в алгоритм предупредительные меры.

2.1.7. Метод простых итераций

Существует простой метод, позволяющий решить уравнение . Рассматриваемое уравнение представляют в виде и находят более точное значение корня по первому приближению с помощью формулы .

Повторяя этот процесс («итерируя») несколько раз, можно получить значения корня с любой степенью точности, если на интервале между корнем уравнения и первым приближением . Если это условие выполняется, то считается, что решение сходится к искомому корню.

При этом сходимость будет более быстрой для малых значений . Поэтому особенно выгодно подобрать, если это возможно, функцию так, чтобы её производная в точке истинного значения корня обращалась в нуль. Если же это условие не выполнимо, то уравнение следует преобразовать (хотя бы переходом к обратной функции). Если , то два смежных приближённых значения корня, полученных путём итерации, будут последовательно больше и меньше корня, что позволяет оценить достигнутую степень точности.

Метод простой итерации относится к числу медленно сходящихся процессов. Поэтому его целесообразно применять для получения значения корня с небольшой точностью, а также для получения более точного результата с использованием одного из способов ускорения итерационных процессов.

Исходя из предположения, что метод может не сойтись, необходимо предусмотреть в программе следующие условия окончания работы:

1. Остановка, как только .

2. Остановка, как только число итераций достигнет N.

Величины 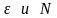задаются.

Алгоритм , реализующий данный метод в сочетании с методом Эйткена, выражается следующей схемой:

1. Вычисление ( )-го приближения по формуле при фиксированном значении (начиная с );

2. Вычисление ( )-го приближения по той же формуле;

3. Проверка достигнутой точности вычислений . Если искомый корень вычислен с нужной степенью точности, то задача считается решенной и управление передаётся оператору п. 5, при недостаточной точности вычислений выполняется оператор п. 4;

4. Вычисление ( )-го приближения по формуле Эйткена

;

5. Окончание вычислений искомого корня.

Пример 1.

PROGRAM Me_Pro_It;

{Решение нелинейных и транцендентных уравнений методом

простых итераций}

{Рассматриваемое уравнение представляется в виде x=f(x). Задают

начальное приближение X0 и уточняют с помощью формулы X1=f(X0).

Повторяют процесс до тех пор, пока не будет достигнута заданная

точность Epsi}

Uses CRT;

Type

Func = Function(a,b,c,X:Real):Real;

Const

a=5.67;

b=4.794;

c=4.5;

Epsi=0.001;

Var

I : Integer;

X0, X, Y : Real;

{$F+}

Function F(a,b,c,X:Real):Real;

{Преобразованная к виду x=f(x) заданная функция}

Begin

F:= a/c*SIN(b*X);

End; {F}

{$F-}

Procedure Iter(a,b,c,Epsi,X0:Real;var X, Y : Real; var I : Integer; F:Func);

Var E:Real;

Begin

X:= X0; {Начальное приближение}

I:=0; {Параметр, позволяющий определить число итераций}

Repeat

I:=I+1;

Y:= F(a,b,c,X);

WriteLn (' Кол. итер.', I:7, ' X= ',X:5:3,' Y= ',Y:5:3);

E:=ABS(Y-X);

X:=Y;

Until (E < Epsi);

End; {Iter}

BEGIN

{Головная программа}

TextBackGround(Black);{Меняет цвет фона на черный, модуль Crt}

ClrScr;{Очищает экран, модуль Crt}

HighVideo; {Устанавливает высокую яркость символов, модуль Crt}

TextColor(LightRed);{Меняет цвет символов на светло-красный, модуль Crt}

WriteLn (' Работает программа Me_Pro_It');

TextColor(Yellow);{Меняет цвет символов на желтый, модуль Crt}

Write (' Введите начальное приближение корня ');

ReadLn (X0);

Iter(a,b,c,Epsi,X0,X, Y,I,F);

TextColor(LightRed);{Меняет цвет символов на светло-красный, модуль Crt}

WriteLn (' **************** РЕЗУЛЬТАТ ****************');

TextColor(LightGreen);{Меняет цвет символов на светло-зеленый, модуль Crt}

WriteLn (' Кол. итер.', I:7, ' X= ',X:5:3,' Y= ',Y:5:3);

NormVideo;{Устанавливает первоначальную яркость символов, модуль Crt}

TextColor(LightGray);{Меняет цвет символов на светло-серый, модуль Crt}

WriteLn (' ДЛЯ ПРОДОЛЖЕНИЯ НАЖМИТЕ ЛЮБУЮ КЛАВИШУ!!!');

Repeat Until KeyPressed; {Ожидает нажатия любой клавиши, модуль Crt}

ClrScr;{Очищает экран, модуль Crt}

END.