2.2.2. Метод Ньютона для снау

Название метод Ньютона применяется к целому семейству методов, для которых собственно метод Ньютона служит базовым прототипом.

Рассмотрим простой пример.

Поскольку , где -начальное приближение, то

и можно получить новое приближение . Продолжая итерационный процесс можно с требуемой точностью приблизиться к одному из решений, например,

Расчетная формула для метода Ньютона может быть получена, если представить в окрестности текущего приближения в виде ряда Тейлора

,

и ограничиться линейными членами, тогда в матричной форме получим

,

где

Рис. 1. Итерация метода Ньютона для .

2.2.2.1. Вариант 1

Применительно к СНАУ получим следующий алгоритм:

1. Выбрать начальный вектор , положить

2. Вычислить вектор 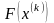. Если все , где e- заданная точность расчета, то получено решение, расчет окончен. Если и 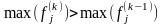, то итерационный процесс расходится, расчет завершить аварийно.

3. Построить матрицу Якоби

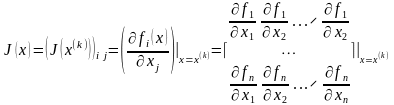
и вычислить значения всех производных в точке .

^{4. Решить систему уравнений, определив} вектор поправок

5. Вычислить новое приближение

и положить .

6. Если , где -заданное предельное число итераций, то аварийно завершить расчет, иначе перейти к п.2 алгоритма.

7. Конец алгоритма.

Метод Ньютона при начальном приближении близком к некоторому решению часто обладает устойчивой квадратичной сходимостью. При плохой начальной точке имеет место расходящийся итерационный процесс. Метод Ньютона расходится, если матрица Якоби плохо обусловлена в окрестности решения. Часто перед использованием метода Ньютона выполняют несколько итераций, например, методом последовательных приближений для того, чтобы иметь «хорошее» начальное приближение.

В качестве косвенного критерия расхождения итерационного процесса можно использовать изменение знака Якобиана - определителя матрицы Якоби. Однако это условие, являясь достаточным, не является необходимым. Якобиан может быть вычислен, как побочный продукт решения методом Гаусса системы из п.3 алгоритма.

2.2.2.2. Вариант 2

Алгоритм:

1. Задаём абсолютную или относительную погрешность , число уравнений , максимальное число итераций и вектор начальных приближений (с компонентами ).

2. Используя разложение в ряд Тейлора, формулируем матрицу Якоби , необходимую для расчёта приращений при малом изменении переменных. Матрица Якоби в развёрнутом виде записывается следующим образом:

Поскольку аналитическое дифференцирование в общем случае нежелательно, заменяем частные производные в матрице Якоби их приближенными конечно-разностными значениями

где - малое приращение , например .

3. Составляем и решаем систему линейных уравнений для малых приращений :

Решение этой системы даёт , т. е. .

4. Вычисляем уточнённые значения

или в общем виде

5. Для всех проверяем одно из условий: по абсолютной и относительной погрешностям.

Если оно выполняется, идём к п. 2, т. е. выполняем новую итерацию. Иначе считаем вектор найденным решением.

ПРИМЕР.

Испытаем метод Ньютона на примере

с . Матрица Якоби имеет вид

,

и уравнение Ньютона имеет вид

Использование гауссова исключения даёт , и поэтому новым приближением к решению будет . Решением же системы нелинейных уравнений является .