
- •Содержание
- •2. Понятие уравнения
- •2.1. Численное решение нелинейных алгебраических и транцендентных уравнений
- •2.1.1. Метод перебора
- •2.1.2. Метод дихотомии (половинного деления)
- •2.1.3. Метод отделения корней
- •2.1.4. Метод хорд
- •2.1.5. Метод касательных (метод Ньютона, метод линеаризованной итерации)
- •2.1.6. Метод секущих (комбинированный метод секущих – хорд, метод хорд - касательных)
- •2.1.7. Метод простых итераций
- •2.2. Численные методы решения систем нелинейных алгебраических уравнений (снау)
- •2.2.1. Метод последовательных приближений (простых итераций) для снау
- •2.2.2. Метод Ньютона для снау
- •2.2.2.1. Вариант 1
- •2.2.2.2. Вариант 2
- •2.2.2.3. Меры предосторожности в методе Ньютона
- •2.2.2.4. Локальное решение нелинейного уравнения
- •2.2.3. Метод Ньютона по параметру
- •2.2.4. Метод Бройдена
- •2.2.5. Метод Матвеева
- •Литература
- •Задания и примеры выполнения нахождение корня нелинейного уравнения
- •1. Постановка задачи
- •2. Методы решения задачи
- •2.1 Метод деления отpезка пополам
- •2.2 Метод простой итерации
- •2.3 Метод Ньютона
- •Методы решения системы нелинейных уравнений
- •Постановка задачи
- •2. Методы решения системы нелинейных уравнений
- •2.1.Метод простой итерации
- •2.2. Метод Ньютона
2.2. Численные методы решения систем нелинейных алгебраических уравнений (снау)
В подавляющем большинстве случаев математические модели реальных объектов содержат нелинейные функции, их отсутствие в математической модели говорит, как правило, о наличии упрощений.
Решение СНАУ является сложной задачей, необходимо глубокое знание, как физических свойств исследуемого объекта, так и особенностей СНАУ, используемых для его описания.
Наибольшее распространение получили методы ньютоновского типа, но могут применяться разные варианты последовательных приближений, градиентные методы и т.п.
СНАУ
будем представлять как равную нулю
вектор-функцию
размерности
,
элементами которого являются функции
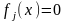 ,
,
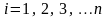 ,
где
-
вектор искомого решения размерности
.
Например,
,
где
-
вектор искомого решения размерности
.
Например,
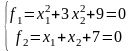
Вариант нелинейного метода наименьших квадратов не рассматривается.
При решении СНАУ, как правило, возникает проблема существования и единственности решения, выбора подходящего решения из множества решений, удовлетворяющих тождеству , если решение существует.
Для большинства задач таких, для которых точное аналитическое решение не может быть получено, необходимо выполнение последовательности итераций. Важным является способ задания начального приближения, а также вопрос о том, будет ли сходиться выбранный метод к одному из решений и насколько быстро.
Говорят,
что последовательность
 сходится к
сходится к
 ,
если
,
если
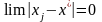 при
при
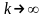 .
.
Если
существует константа
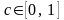 и целое
и целое
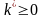 ,
такие, что для всех
,
такие, что для всех
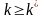
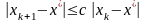 ,
,
то
говорят, что последовательность
 линейно сходится
к
.
линейно сходится
к
.
Если
данное неравенство выполняется для
некоторой последовательности
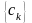 ,
сходящейся к нулю, то говорят, что
сходится
сверхлинейно к
.
,
сходящейся к нулю, то говорят, что
сходится
сверхлинейно к
.
Если
сходится к
и существуют
постоянные
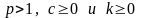 ,
такие, что для всех
,
такие, что для всех
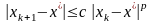 ,
,
то
говорят, что
сходится к
с порядком, по
меньшей мере равным
.
При
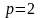 говорят
о квадратичной
скорости сходимости.
говорят
о квадратичной
скорости сходимости.
Итерационный метод, сходящийся с определенной скоростью к истинному решению при условии, что он стартует в достаточной близости от этого решения, называется локально сходящимся.
Под глобально сходящимися часто понимают методы, в которых обеспечивается сходимость к некоторому решению системы нелинейных уравнений почти из любой начальной точки.
2.2.1. Метод последовательных приближений (простых итераций) для снау
Метод
последовательных приближений применяется
в тех случаях, когда каждая из функций
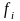 может
быть аналитически разрешена относительно
,
т.е. система уравнений приводима к виду
может
быть аналитически разрешена относительно
,
т.е. система уравнений приводима к виду
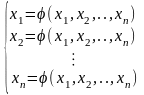
Алгоритм решения заключается в последовательном вычислении
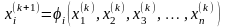
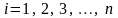 и
и
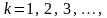 начиная с некоторого начального
приближения
,
пока:
начиная с некоторого начального
приближения
,
пока:
будет выполнено условие
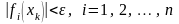 ,
где e-
заданная точность расчета, т.е. получено
некоторое решение;
,
где e-
заданная точность расчета, т.е. получено
некоторое решение;зарегистрирован факт расхождения итерационного процесса;
превышено заданное предельное число итераций.
Для сходимости итерационного процесса достаточно, чтобы вблизи истинных значений корней выполнялись неравенства
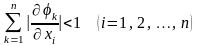 .
.
Метод
простых итераций рекомендуется применять
в тех случаях, когда исходная система
легко преобразуется к виду
 и известно хорошее начальное приближение.
и известно хорошее начальное приближение.
Необходим глубокий анализ вида системы в каждом отдельном случае с точки зрения сходимости метода, возможности получения желаемого решения с требуемой точностью. Как правило, метод последовательных приближений является, в лучшем случае, линейно сходящимся.
В качестве вариантов метода последовательных приближений можно указать рассмотренные методы простой и ускоренной (метод Зейделя) итерации, модифицированные с учетом нелинейности решаемой задачи.
