Алгоритм классического метода Гаусса для ленточной симметричной матрицы
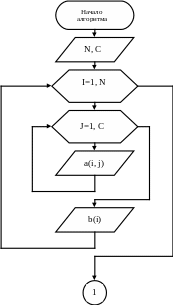
Рис. 1.3а. Алгоритм ввода ленточной матрицы для классического метода Гаусса.
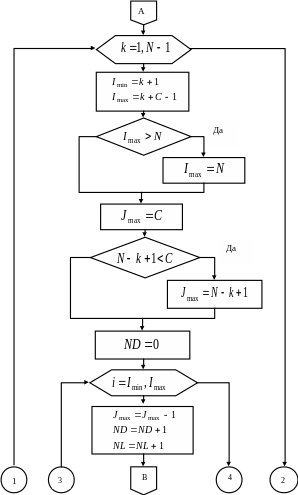
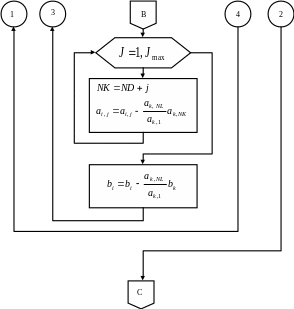
Рис. 1.3б. Алгоритм прямого хода для классического метода Гаусса.
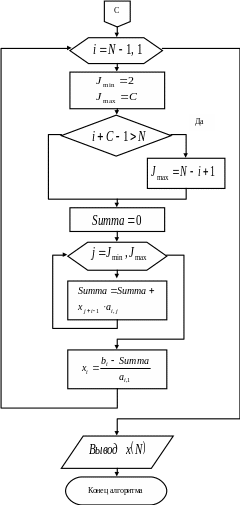
Рис. 1.3в. Алгоритм обратного хода для классического метода Гаусса.
Рассмотрим несимметричную ленточную матрицу и применительно к ней классический метод Гаусса.
Исходная ленточная несимметричная матрица [9x9]. Ширина полосы=5 |
|
Способ хранения ленточной несимметричной матрицы [9x5]. Ширина полосы=5 |
||||||||||||||||||
Коэффициенты матрицы |
|
Коэффициенты матрицы |
|
|||||||||||||||||
9 |
1 |
2 |
3 |
4 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
9 |
1 |
2 |
3 |
4 |
1 |
|
1 |
9 |
1 |
2 |
3 |
4 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
1 |
9 |
1 |
2 |
3 |
4 |
2 |
|
1 |
1 |
9 |
1 |
2 |
3 |
4 |
0 |
0 |
3 |
0 |
0 |
1 |
1 |
9 |
1 |
2 |
3 |
4 |
3 |
|
1 |
1 |
1 |
9 |
1 |
2 |
3 |
4 |
0 |
4 |
0 |
1 |
1 |
1 |
9 |
1 |
2 |
3 |
4 |
4 |
|
1 |
1 |
1 |
1 |
9 |
1 |
2 |
3 |
4 |
5 |
1 |
1 |
1 |
1 |
9 |
1 |
2 |
3 |
4 |
5 |
|
0 |
1 |
1 |
1 |
1 |
9 |
1 |
2 |
3 |
6 |
1 |
1 |
1 |
1 |
9 |
1 |
2 |
3 |
0 |
6 |
|
0 |
0 |
1 |
1 |
1 |
1 |
9 |
1 |
2 |
7 |
1 |
1 |
1 |
1 |
9 |
1 |
2 |
0 |
0 |
7 |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
9 |
1 |
8 |
1 |
1 |
1 |
1 |
9 |
1 |
0 |
0 |
0 |
8 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
9 |
9 |
1 |
1 |
1 |
1 |
9 |
0 |
0 |
0 |
0 |
9 |
|
Пример 1.12 (для несимметричных матриц).
program GAUSSLe;
{Решение СЛАУ классическим методом Гаусса }
{ЛЕНТОЧНАЯ НЕСИММЕТРИЧНАЯ МАТРИЦА, хранится в виде прямоугольника}
{Прямой ход исключения переменных}
For k:= 1 to N-1 do
begin
Imin:= k+1;
Imax:= k+C-1;
If Imax > N Then Imax:= N;
For i:= Imin to Imax do
begin
Jmin:= C-(i-k);
Jmax:= 2*C-1-(i-k);
Q:= - a[i,k+C-i]/a[k,C];
For j:= Jmin to Jmax do
a[i,j]:= a[i,j] + a[k,j+(i-k)] * Q;
b[i]:= b[i] + b[k] * Q;
end;
end;
{Обратный ход: последовательное нахождение корней }
x[N]:= b[N]/a[N,C];
For i:= N-1 downto 1 do
begin
Jmin:= C+1;
Jmax:= 2*C-1;
If i > N-C Then Jmax:= N+C-i;
Summa:= 0;
For j:= Jmin to Jmax do Summa:= Summa + x[j+i-C]*a[i,j];
x[i]:= (b[i]-Summa)/a[i,C];
end;
Рассмотрим симметричную ленточную матрицу и применительно к ней метод Холесского.
Исходная ленточная симметричная матрица [9x9]. Ширина полосы=5 |
|
Способ хранения ленточной симметричной матрицы [9x5]. Ширина полосы=5 |
||||||||||||||
Коэффициенты матрицы |
|
Коэффициенты матрицы |
|
|||||||||||||
9 |
1 |
2 |
3 |
4 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
9 |
1 |
|
1 |
9 |
1 |
2 |
3 |
4 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
1 |
9 |
2 |
|
2 |
1 |
9 |
1 |
2 |
3 |
4 |
0 |
0 |
3 |
0 |
0 |
2 |
1 |
9 |
3 |
|
3 |
2 |
1 |
9 |
1 |
2 |
3 |
4 |
0 |
4 |
0 |
3 |
2 |
1 |
9 |
4 |
|
4 |
3 |
2 |
1 |
9 |
1 |
2 |
3 |
4 |
5 |
4 |
3 |
2 |
1 |
9 |
5 |
|
0 |
4 |
3 |
2 |
1 |
9 |
1 |
2 |
3 |
6 |
4 |
3 |
2 |
1 |
9 |
6 |
|
0 |
0 |
4 |
3 |
2 |
1 |
9 |
1 |
2 |
7 |
4 |
3 |
2 |
1 |
9 |
7 |
|
0 |
0 |
0 |
4 |
3 |
2 |
1 |
9 |
1 |
8 |
4 |
3 |
2 |
1 |
9 |
8 |
|
0 |
0 |
0 |
0 |
4 |
3 |
2 |
1 |
9 |
9 |
4 |
3 |
2 |
1 |
9 |
9 |
|
Рассмотрим метод Холесского применительно к полностью хранимой матрице.
Пример 1.13 (для симметричных матриц).
program Cholessky;
{Решение СЛАУ методом Холесского }
{ЛЕНТОЧНАЯ МАТРИЦА, хранится полностью}
Uses CRT;
Const
NameFile = 'D:\PASCAL\PRIMER\CHOLES\Sim.dat';
NameOut = 'D:\PASCAL\PRIMER\CHOLES\CholKlas.out';
Type
RealType = Real;
IntType = Byte;
Var
a, a1 : array [1..9,1..9] of RealType;
b, b1, x : array [1..9] of RealType;
sum, eps : RealType;