1. Вектордың анықтамасы. Тең векторлардың анықтамасы.
Бағытталған кесінді деп A — “бас нүктесінен” бастап екінші B - “соңғы”нүктесіне дейінгі түзу бойындағы нүктелер жиыны. Жәй мағынасына сәйкес вектор деп бағытталғын кесінді деп түсінуге болады, ал басқа жағдайларда әр-түрлі векторлар – белгілі бір эквиваленттік қатынасы бойынша әр-түрлі бағытталған кесінділер эквивалентті класстары болып табылады. Бұл эквиваленттік қатынасы әр-түрлі болуы мүмкін: ол векторлардың түрін анықтайды (“еркін”, “тұрақты” т.б.). Басқаша айтқанда, эквивалентті класс ішінде кез келген екі вектор тең болып есептеледі, яғни кез келген вектор сол класты толықтай бейнелей алады.
Еркін векторлар жиыны мен олардың кеңістікті параллель жылжыту жиыны арасындағы изоморфизмды ескерсе, егерде қосу операциясын жылжыту композицияларымен теңестірсе, онда кеңістікті параллель жылжыту жиынын тіпті векторды анықтау үшін де пайдалануғы болады. Кеңістікті шексіз аз трансформацияларын зерттеуде маңызды рөл атқарады.
Бaс нүктесі соңғы нүктесімен беттесетін векторды нөль-вектор деп атайды: векторын векторына қарсы вектор деп атайды.
2. Векторларды қосу амалының анықтамасы. Векторларды қосу амалының қасиеттерін дәлелдеу.
Екі u, v векторлары және олардың қосындысы
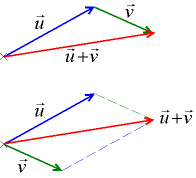
Екі векторларды қосуды параллелограмм ережесімен де, үшбұрыш ережесімен де іске асыруға болады.
Үшбұрыш ережесі. Екі мен векторларын үшбұрыш ережесімен қосу үшін осы екі векторды өздеріне біреуінің бас жағы екіншісінің аяғымен беттесетіндей параллель көшіру керек. Сонда пайда болған үшбұрыштың үшінші қабырғасы бас жағы алғашқы вектордың басымен беттесетін бастапқы екі вектордың қосынды векторы болып табылады.
Параллелограмм ережесі. Екі мен векторларын параллелограмм ережесімен қосу үшін екеуін де бастары беттесетіндей параллель көшіріп параллелограммға болықтырады. Сонда екеуінің қосындысы деп параллелограммның осы екі вектор бас жағынан шығатын диагоналін айтады.
Екі сырғанақ векторларды қосу тек қана олар жатқан екі түзу қиылысқанда ғана анықталған. Бұл жағдайда әр вектор өз түзуі бойымен қиылысу нүктесіне дейін көшіріліп, содан кейін параллелограмм ережесімен қосылады.
Екі тұрақты векторларды қосу тек егер олардың ортақ бас нүктесі болғанда ғана анықталған. Бұл жағдайда да олар параллелограмм ережесімен қосылады.
3. Векторды санға көбейту амалының анықтамасы. Векторды санға көбейту амалының қасиеттерін дәлелдеу.
векторы
мен λ санының көбейтіндісі леп
деп беліленетін, модулі тең
, ал бағыты
векторының бағытымен бірдей , егер
болса, және керісінше, қарсы бағытталады,
егер
болса. Егер
, немесе
вектор
нөлдік
болса,
тек
осы
жағдайда
ғана
көбейтінді
де
—
нөлдік
вектор.
Әдетте
бұл көбейтіндіні жазғанда бірінші санды
сосын векторды жазады, дегенмен де
керісінше жазу да қате емес. Қалай десек
те,
.
Векторды санға көбейту амалы және оның қасиеттері.
Нөлдік емес а векторының α нақты санына көбейтіндісі деп,α>0 болғанда бағыты а-ның бағытымен бағыттас ,ал α<0 болғанда бағыты оған қарама-қарсы болатын а-ға коллинеар векторды атайды.Бұл вектордың ұзындығы а векторының ұзындығы мен α саны абсолют шамасының көбейтіндісіне тең болады, а векторының α санына көбейтіндісі а*α арқылы белгіленді.
а=Ө немесе α= 0 жағдайлар үшін қосымша анықтама береміз,кез-келген α үшін α*Ө=Ө кез-келген а үшін 0*а=Ө,
Кез-келген α,β сандары және а,в бағытталған кесінділері үшін мынандай қасиеттер орындалады:1)1*a=a: 2)α*(a*β)=(α*β)*a векторды санға көбейту ассоцативті:
3)(α+β)*a=α*a+β*a векторларды санға көбейту амалы сандарды қосуға қатысты дистрибутивті:4)α*(a+b)=α*a+α*b векторларды санға көбейту векторларды қосуға қатысты дистрибутивті ,1) дәлелдеудің қажеті жоқ,2 –ні дәлелдеу а вектор арқылы L түзуін жүргізіп ,оның бір бағытын оң деп есептейік, а векторын ,сонымен қатар β*α,α*(β*a).(α*β)*a векторларын осы түзудің бойында деп алайық,3-ші теореманың бірінші тұжырымы бойынша α*(β*α)=(α*β)*a векторлар тендігінің орнына ,{α*(β*a)}={(α*β)*a} шамаларының тендігін дәлелдейік:
{α*(β*a)}=α*{β*a}=α*(β*{a})=(α*β){a}={(α*β)*a}
3)дәлелдеу {(α+β)*a}={α+β}*a=({α}+{β})*a={α}+a+{β}*a
4)дәлелдеу
{α*(a+b)}=α*{a+b}=α*({a}+{b})=α*{a}+α*{b}.Барлық қасиеттер дәлелденді.