
- •Эквивалентность слау при элементарных преобразованиях
- •Описание
- •Достоинства метода
- •Следствия
- •Свойства определителей
- •10. Теорема о разложении определителей по строкам, по столбцам:
- •Формулировка
- •Разложение определителя по строке (столбцу) (Следствие 1)
- •Следствие 2 (фальшивое разложение определителя)
- •11. Теорема Крамера
- •Описание метода
- •Вычислительная сложность
- •12. Теорема о определителях произведении матриц?
- •13. Теорема о нахождении обратной матрицы с помощью алгебраической дополнении
- •14. Нахождение обратной матрицы с помощью элементарной преобразовании
- •15. Поле комплексных чисел. Алгебраическая формула комплексных чисел
- •Алгебраическая форма
- •18. Нахождения корня комплексного числа в тригонометрической форме?
- •Операции над многочленами.
- •21. Деление с остатком в кольце многочленов?
- •22. Алгоритм Евклида в кольце многочленов?
- •23. Нод и нок двух многочленов?
- •24. Корни многочленов. Простые и кратные формы?
- •25. Деление многочленов на двух член! Схема Хорнера?
- •26 Неприводимый многочлен и их свойства
- •Определение
- •Свойства
- •27 Основная теорема поля комплексных чисел без доказательства и ее следствия
- •Некоторые следствия из аксиом поля
- •Определение поля комплексных чисел
- •28 Неприводимые многочлены над полем действительных чисел?
- •Определение
- •Свойства
- •Примеры
- •Конечные поля
- •29 Неприводимые многочлены над полем рациональных чисел. Критерий Эйзенштейна?
- •30 Векторная пространства. Линейная оболочка векторов?
- •31. Базис и ранг системы векторов?
- •32. Линейная зависимость и линейная независимость систем векторов
- •33. Признаки линейной зависимости векторов
- •34 Необходимые и достаточные условия линейной независимости систем векторов?
- •35 Линейная зависимость двух векторов на прямой
- •36 Линейная зависимость трех векторов на плоскости
- •37 Линейная зависимость четырех векторов в пространстве
- •38 . Базис и размерность над пространством
- •39 Координаты вектора в данном базисе . Координаты точки
- •40 Скалярное произведение векторов свойства
- •2.Свойтсва скалярного произведения векторов.
- •43. Геометрический смысл скалярного, векторного и смешанного произведения.
- •Геометрические свойства векторного произведения
- •44.Аффинная система координат. Прямоугольная система координат?
- •45 Радиус Вектора Расстояние между двумя точками
- •46 Уравнение прямой на плоскости
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и направляющему вектору
- •47 Нормальный и направляющий вектор на прямой
- •48 Расположение двух прямых Условия параллельности и перпендикулярности прямых
- •49.Угол между двумя прямыми
- •50.Расстояние от точки до прямой
1 Множество и операции над ними
Понятие множества является исходным (основным) всей математики в целом, то есть не определяется через математические понятия.
Содержание понятия множество может быть раскрытым. Так можно говорить о множестве студентов, жителей города.
Обычно множество обозначается заглавными буквами латинского алфавита, а предметы, составляющие это множество (его элементы) малыми буквами. За некоторыми часто встречающимися в математике множествами закреплены постоянные знаки.
N– множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
R – множество действительных чисел;
C – множество комплексных чисел;
Тот факт, что x является элементом множества X записывается так: x∈A .
Если y не является элементом множества Y, то это записывается так: y/∈A .
Если множество не содержит элементов, то его будем называть пустым множеством и обозначать ⊘ .
Определение. Два множества A и B, состоящие из одних и тех же элементов называются равными, то есть A=B.
Определение. Множество A называется подмножеством B, если каждый элемент множества Aявляется элементом и множества B. Обозначение: A⊆B .
Определение. Если в B есть хотя бы один элемент, не принадлежащий A, то множество A называется собственным подмножеством множества B. Обозначение: A⊂B .
Пустое множество является подмножеством любого множества.
Любое множество A имеет 2 несобственных подмножества: A и ⊘ .
Очевидно, что если A - подмножество B и B - подмножество A, то A=B.
Определение. Объединением множеств A и B называется множество, которое состоит из всех тех элементов, каждый из которых является элементом хотя бы одного из множеств A или B. Обозначение: A⋃B .
Определение. Пересечением множеств A и B называется множество, которое состоит из всех общих элементов множества A и B. Обозначение: A⋂B .
Свойства операция объединения и пересечения множеств. 1) коммутативность объединения и пересечения множеств A⋃B=B⋃A ; A⋂B=B⋂A . 2) ассоциативность объединения и пересечения множеств A⋃(B⋃C)=(A⋃B)⋃C ; A⋂(B⋂C)=(A⋂B)⋂C ; 3) дистрибутивность A⋂(B⋃C)=(A⋂B)⋃(A⋂C) ; Определение. Разностью множеств A и B называется множество, которое состоит из элементов множества A, не входящих в B. Обозначение: A∖B .
Если B - есть подмножество A, то разность A∖B называют дополнением множества B до A. Обозначение: CAB.
2 Функции и их отношения?
Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Математическое
понятие функции выражает интуитивное
представление о том, как одна величина полностью
определяет значение другой величины.
Так значение переменной ![]() однозначно
определяет значение выражения
однозначно
определяет значение выражения ![]()
Часто под термином «функция» понимается числовая функция; то есть функция которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.
Функция ![]() (отображение, операция, оператор) —
это закон или правило,
согласно которому каждому[3] элементу
из
множества
(отображение, операция, оператор) —
это закон или правило,
согласно которому каждому[3] элементу
из
множества ![]() ставится
в соответствие единственный элемент
ставится
в соответствие единственный элемент ![]() из
множества
из
множества ![]() .[4]
.[4]
При этом говорят, что функция задана на множестве , или что отображает в .
Если
элементу ![]() сопоставлен
элемент
сопоставлен
элемент ![]() ,
то говорят, что элемент
находится
в функциональной
зависимости
от
элемента
.
При этом переменная
называется
аргументом функции
или независимой переменной,
множество
называется областью
задания или областью
определения функции,
а элемент
,
соответствующий конкретному
элементу
— частным
значением функции
в
точке
.
Множество
всех
возможных частных значений
функции
называется
её областью
значений илиобластью
изменения.
,
то говорят, что элемент
находится
в функциональной
зависимости
от
элемента
.
При этом переменная
называется
аргументом функции
или независимой переменной,
множество
называется областью
задания или областью
определения функции,
а элемент
,
соответствующий конкретному
элементу
— частным
значением функции
в
точке
.
Множество
всех
возможных частных значений
функции
называется
её областью
значений илиобластью
изменения.
Если задана функция , которая определена на множестве и принимает значения в множестве , то есть, функция отображает множество в , то
этот факт коротко записывают в виде
 или
или 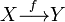 .
.область определения функции (множество ) обозначается
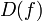 ,
или
,
или 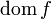 ;
;область значений функции (множество ) обозначается
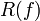 (
(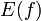 ),
или
),
или 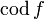 (
(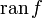 ).
).
Наличие функциональной зависимости между элементом и элементом
наиболее часто обозначается как
![]() ,
,
![]() или
или
![]() ;
;
реже используется обозначение без скобок
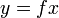 ,
, 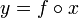 или
или 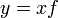 ,
,а там, где необходимо подчеркнуть двойственность, используются обозначения со скобками:
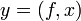 или
или 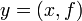 ;
;так же существует и операторное обозначение
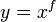 ,
которое можно встретить в общей
алгебре.
,
которое можно встретить в общей
алгебре.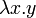 в лямбда-исчислении Чёрча
в лямбда-исчислении Чёрча
3 Перестановка и их свойства
Перестановкой
чисел 1, 2,..., n называется любое расположение
этих чисел в определенном порядке. В
элементарной алгебре доказывается, что
число всех перестановок, которые можно
образовать из n чисел, равно 12...n = n!.
Например, из трех чисел 1, 2, 3 можно
образовать 3!=6 перестановок: 123, 132, 312,
321, 231, 213. Говорят, что в данной перестановке
числа i и j составляют инверсию (беспорядок),
если i>j, но i стоит в этой перестановке
раньше j, то есть если большее число
стоит левее меньшего.Перестановка
называется четной (или нечетной), если
в ней соответственно четно (нечетно)
общее число инверсий. Операция, посредством
которой от одной перестановки переходят
к другой, составленной из тех же n чисел,
называется подстановкой n-ой
степени.В комбинаторике перестано́вка —
это упорядоченный
набор чисел ![]() обычно
трактуемый как биекция на
множестве
обычно
трактуемый как биекция на
множестве ![]() ,
которая числу i ставит
соответствиеi-й
элемент из набора. Число n при
этом называется порядком перестановки.
,
которая числу i ставит
соответствиеi-й
элемент из набора. Число n при
этом называется порядком перестановки.
В теории групп под перестановкой (подстановкой) произвольного множества подразумевается биекция этого множества на себя.
Число всех перестановок порядка
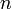 равно
числу размещений из n по n,
то есть факториалу:[1][2][3][4]
равно
числу размещений из n по n,
то есть факториалу:[1][2][3][4]
![]()
Композиция определяет операцию произведения на перестановках одного порядка:
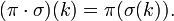 Относительно
этой операции множество перестановок
порядка nобразует группу,
которую называют симметрической и
обычно обозначают
Относительно
этой операции множество перестановок
порядка nобразует группу,
которую называют симметрической и
обычно обозначают 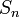 .
.Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элемент
 сопоставляется
с перестановкой
сопоставляется
с перестановкой 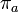 ,
задаваемой тождеством
,
задаваемой тождеством  где g —
произвольный элемент группы G,
а
где g —
произвольный элемент группы G,
а  —
групповая операция.
—
групповая операция.Инволюция — перестановка
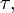 которая
является обратной самой себе, то есть
которая
является обратной самой себе, то есть 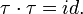
Беспорядок — перестановка без неподвижных точек.
Циклом длины
 называется
такая подстановка
называется
такая подстановка  которая
тождественна на всём множестве
которая
тождественна на всём множестве 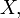 кроме
подмножества
кроме
подмножества 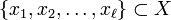 и
и  Обозначается
Обозначается 
Транспозиция — перестановка элементов множества , которая меняет местами два элемента. Транспозиция является циклом длины 2.
Рассмотрим n элементов m различных
типов, причем в каждом типе все элементы
одинаковы. Тогда перестановки из всех
этих элементов с точностью до порядка
следования однотипных элементов
называются перестановками
с повторением.
Если ki —
количество элементов i-го
типа, то ![]() и
количество всевозможных перестановок
с повторениями равно мультиномиальному
коэффициенту
и
количество всевозможных перестановок
с повторениями равно мультиномиальному
коэффициенту ![]()
4. Матрицы и операции над ними
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы[1], в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Для матрицы определены следующие алгебраические операции:
сложение матриц, имеющих один и тот же размер;
умножение матриц подходящего размера (матрицу, имеющую столбцов, можно умножить справа на матрицу, имеющую строк);
в том числе умножение на матрицу вектора (по обычному правилу матричного умножения; вектор является в этом смысле частным случаем матрицы);
умножение матрицы на элемент основного кольца или поля (т. е. скаляр).
Сложение
матриц ![]() есть
операция нахождения матрицы
есть
операция нахождения матрицы ![]() ,
все элементы которой равны попарной
сумме всех соответствующих элементов
матриц
,
все элементы которой равны попарной
сумме всех соответствующих элементов
матриц ![]() и
и ![]() ,
то есть каждый элемент матрицы
равен
,
то есть каждый элемент матрицы
равен
![]()
Свойства сложения матриц:
1.коммутативность: A+B = B+A;
2.ассоциативность: (A+B)+C =A+(B+C);
3.сложение с нулевой матрицей: A + Θ = A;
4.существование противоположной матрицы: A + (-A) = Θ;
Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:
Множество всех матриц одинаковых размеров mxn с элементами из поля P (поля всех действительных или комплексных чисел) образуют линейное пространство над полем P (каждая такая матрица является вектором этого пространства). Впрочем, прежде всего во избежание терминологической путаницы, матрицы в обычных контекстах избегают без необходимости (которой нет в наиболее обычных стандартных применениях) и четкого уточнения употребления термина называть векторами.
Умножение матриц
Умножение
матриц (обозначение: ![]() ,
реже со знаком умножения
,
реже со знаком умножения ![]() ) —
есть операция вычисления матрицы
,
элементы которой равны сумме произведений
элементов в соответствующей строке
первого множителя и столбце второго.
) —
есть операция вычисления матрицы
,
элементы которой равны сумме произведений
элементов в соответствующей строке
первого множителя и столбце второго.
![]()
Количество
столбцов в матрице
должно
совпадать с количеством строк в матрице
,
иными словами, матрица
обязана
быть согласованной с
матрицей
.
Если матрица
имеет
размерность ![]() ,
—
,
— ![]() ,
то размерность их произведения
,
то размерность их произведения ![]() есть
есть ![]() .
.
Свойства умножения матриц:
1.ассоциативность (AB)C = A(BC);
2.некоммутативность (в общем случае): AB
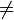 BA;
BA;
3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;
4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;
5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);
Умножение вектора на матрицу
По обычным правилам матричного умножения осуществляется умножение на матрицу слева вектора-столбца, а также умножение вектора-строки на матрицу справа. Поскольку элементы вектора-столбца или вектора-строки можно записать (что обычно и делается), используя один, а не два индекса, это умножение можно записать так:
для вектора-столбца v (получая новый вектор-столбец Av):
![]()
для вектора-строки s (получая новый вектор-строку sA):
![]()
Вектор-строка, матрица и вектор столбец могут быть умножены друг на друга, давая число (скаляр):
![]()
(Порядок важен: вектор-строка слева, вектор-столбец справа от матрицы).
Эти операции являются основой матричного представления линейных операторов и линейных преобразований координат (смены базисов), таких, как повороты, масштабирования, зеркальные отражения, а также (последнее) матричного представления билинейных (квадратичных форм.
При представлении вектора вещественного векторного пространства в ортонормированном базисе (что эквивалентно использованию прямоугольных декартовых координат) соответствующие ему вектор-столбец и вектор-строка, представляющие собой набор компонент вектора, будут совпадать (поэлементно), отличаясь лишь формально своим изображением для корректности матричных операций (т.е. один получается из другого просто операцией транспонирования). При использовании же неортонормированных базисов (например, косоугольных координат или хотя бы разных масштабов по осям) вектор-столбец соответствует компонентам вектора в основном базисе, а вектор-строка - в базисе, дуальном основному [4] (Иногда о пространстве векторов-строк говорят также как об особом, дуальном пространству векторов-столбцов, пространстве ковекторов).
Заметим, что обычной мотивировкой введения матриц и определения операции матричного умножения (см.тж.в статье об умножении матриц) является именно введение их, начиная с умножения вектора на матрицу (которое вводится исходя из преобразований базиса или вообще линейных операций над векторами), а уже затем композиции преобразований сопоставляется произведение матриц. Действительно, если новый вектор Av, полученный из исходного вектора v преобразованием, представимым умножением на матрицу A, преобразовать теперь еще раз, преобразованием, представимым умножением на матрицу B, получив B(Av), то, исходя из правила умножения вектора на матрицу, приведенного в начале этого параграфа (используя ассоциативность умножения чисел и меняя порядок суммирования), нетрудно увидеть в результате формулу, дающую элементы матрицы (BA), представляющую композицию первого и второго преобразований, и совпадающую с обычным определением матричного умножения.
5 Ступенчатый вид матрицы
В линейной алгебре матрица считается матрицей ступенчатого вида по строкам если
все ненулевые строки (имеющие по крайней мере один ненулевой элемент) располагаются над всеми чисто нулевыми строками;
ведущий элемент (первый ненулевой элемент строки при отсчёте слева направо) каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.
Вот пример матрицы ступенчатого вида по строкам:
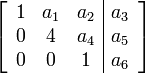
Матрица называется матрицей приведенного ступенчатого вида по строкам (или канонического вида по строкам) если она удовлетворяет дополнительному условию:
каждый ведущий элемент ненулевой строки - это единица и он является единственным ненулевым элементом в своём столбце.
Вот пример матрицы приведенного ступенчатого вида по строкам:
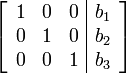
Отметим, что левый край матрицы приведенного ступенчатого вида по строкам не обязательно имеет вид единичной матрицы. Например, следующая матрица является матрицей приведенного ступенчатого вида

поскольку константы в третьем столбце не являются ведущими элементами своих строк.
Приведение матриц к ступенчатому виду
Просмотреть статью: Ступенчатый вид по строкам
Введём понятие ступенчатых матриц:
Матрица имеет ступенчатый вид, если:
Все нулевые строки матрицы стоят последними;
Для любой ненулевой строки матрицы (пусть для определённости её номер равен
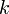 )
справедливо следующее: если
)
справедливо следующее: если 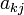 —
первый ненулевой элемент строки
,
то
—
первый ненулевой элемент строки
,
то 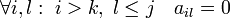 .
.
Тогда справедливо следующее утверждение:
|
Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду. |
6. . Элементарные преобразование. Ранг матрицы
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.
Элементарными преобразованиями строк называют:
перестановка местами любых двух строк матрицы;
умножение любой строки матрицы на константу ,
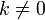 ;
;прибавление к любой строке матрицы другой строки.
Аналогично определяются элементарные преобразования столбцов.
Элементарные преобразования обратимы.
Обозначение ![]() указывает
на то, что матрица
может
быть получена из
путём
элементарных преобразований (или
наоборот).
указывает
на то, что матрица
может
быть получена из
путём
элементарных преобразований (или
наоборот).
Теорема
(об инвариантности ранга при
элементарных преобразованиях).
Если
,
то ![]()
Эквивалентность слау при элементарных преобразованиях
Назовём элементарными преобразованиями над системой линейных алгебраических уравнений:
перестановку уравнений;
умножение уравнения на ненулевую константу;
сложение одного уравнения с другим, умноженным на некоторую константу.
Т.е. элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:
Теорема (об эквивалентности систем уравнений при элементарных преобразованиях). Система линейных алгебраических уравнений, полученная путём элементарных преобразований над исходной системой, эквивалентна ей.
Ранг матрицы
Рангом системы
строк (столбцов) матрицы
с ![]() строк
и
столбцов
называется максимальное число линейно
независимых строк
(столбцов). Несколько строк (столбцов)
называются линейно независимыми, если
ни одна из них не выражается линейно
через другие. Ранг системы строк всегда
равен рангу системы столбцов, и это
число называется рангом матрицы.
строк
и
столбцов
называется максимальное число линейно
независимых строк
(столбцов). Несколько строк (столбцов)
называются линейно независимыми, если
ни одна из них не выражается линейно
через другие. Ранг системы строк всегда
равен рангу системы столбцов, и это
число называется рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Ранг
матрицы —
Размерность образа ![]() линейного
оператора,
которому соответствует матрица.
линейного
оператора,
которому соответствует матрица.
Обычно
ранг матрицы
обозначается ![]() (
(![]() )
или
)
или ![]() .
Оба обозначения пришли к нам из иностранных
языков, потому и употребляться могут
оба. Последний вариант свойственен
для английского языка,
в то время как первый —
для немецкого, французского и
ряда других языков
.
Оба обозначения пришли к нам из иностранных
языков, потому и употребляться могут
оба. Последний вариант свойственен
для английского языка,
в то время как первый —
для немецкого, французского и
ряда других языков
Пусть ![]() —
прямоугольная матрица.
—
прямоугольная матрица.
Тогда по определению рангом матрицы является:
ноль, если — нулевая матрица;
число
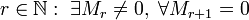 ,
где
,
где 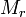 —
минор матрицы
порядка
—
минор матрицы
порядка  ,
а
,
а  —
окаймляющий к нему минор порядка
—
окаймляющий к нему минор порядка 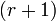 ,
если они существуют.
,
если они существуют.Теорема (о корректности определения рангов). Пусть все миноры матрицы порядка равны нулю (
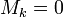 ).
Тогда
).
Тогда 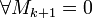 ,
если они существуют.
,
если они существуют.
Существует несколько методов нахождения ранга матрицы:
Метод элементарных преобразований
Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.
Метод окаймляющих миноров
Пусть
в матрице
найден
ненулевой минор
-го
порядка ![]() .
Рассмотрим все миноры
.
Рассмотрим все миноры ![]() -го
порядка, включающие в себя (окаймляющие)
минор
;
если все они равны нулю, то ранг матрицы
равен
.
В противном случае среди окаймляющих
миноров найдется ненулевой, и вся
процедура повторяется.
-го
порядка, включающие в себя (окаймляющие)
минор
;
если все они равны нулю, то ранг матрицы
равен
.
В противном случае среди окаймляющих
миноров найдется ненулевой, и вся
процедура повторяется.
Свойства:
Теорема (о базисном миноре): Пусть
 —
базисный минор матрицы
,
тогда:
—
базисный минор матрицы
,
тогда:базисные строки и базисные столбцы линейно независимы;
любая строка (столбец) матрицы есть линейная комбинация базисных строк (столбцов).
Следствия:
Если ранг матрицы равен , то любые
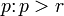 строк
или столбцов этой матрицы будут линейно
зависимы.
строк
или столбцов этой матрицы будут линейно
зависимы.Если — квадратная матрица, и
 ,
то строки и столбцы этой матрицы линейно
зависимы.
,
то строки и столбцы этой матрицы линейно
зависимы.Пусть
 ,
тогда максимальное количество линейно
независимых строк (столбцов) этой
матрицы равно
.
,
тогда максимальное количество линейно
независимых строк (столбцов) этой
матрицы равно
.
Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если , то их ранги равны.
