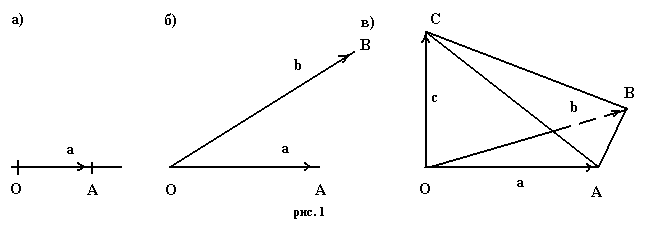
- •Эквивалентность слау при элементарных преобразованиях
- •Описание
- •Достоинства метода
- •Следствия
- •Свойства определителей
- •10. Теорема о разложении определителей по строкам, по столбцам:
- •Формулировка
- •Разложение определителя по строке (столбцу) (Следствие 1)
- •Следствие 2 (фальшивое разложение определителя)
- •11. Теорема Крамера
- •Описание метода
- •Вычислительная сложность
- •12. Теорема о определителях произведении матриц?
- •13. Теорема о нахождении обратной матрицы с помощью алгебраической дополнении
- •14. Нахождение обратной матрицы с помощью элементарной преобразовании
- •15. Поле комплексных чисел. Алгебраическая формула комплексных чисел
- •Алгебраическая форма
- •18. Нахождения корня комплексного числа в тригонометрической форме?
- •Операции над многочленами.
- •21. Деление с остатком в кольце многочленов?
- •22. Алгоритм Евклида в кольце многочленов?
- •23. Нод и нок двух многочленов?
- •24. Корни многочленов. Простые и кратные формы?
- •25. Деление многочленов на двух член! Схема Хорнера?
- •26 Неприводимый многочлен и их свойства
- •Определение
- •Свойства
- •27 Основная теорема поля комплексных чисел без доказательства и ее следствия
- •Некоторые следствия из аксиом поля
- •Определение поля комплексных чисел
- •28 Неприводимые многочлены над полем действительных чисел?
- •Определение
- •Свойства
- •Примеры
- •Конечные поля
- •29 Неприводимые многочлены над полем рациональных чисел. Критерий Эйзенштейна?
- •30 Векторная пространства. Линейная оболочка векторов?
- •31. Базис и ранг системы векторов?
- •32. Линейная зависимость и линейная независимость систем векторов
- •33. Признаки линейной зависимости векторов
- •34 Необходимые и достаточные условия линейной независимости систем векторов?
- •35 Линейная зависимость двух векторов на прямой
- •36 Линейная зависимость трех векторов на плоскости
- •37 Линейная зависимость четырех векторов в пространстве
- •38 . Базис и размерность над пространством
- •39 Координаты вектора в данном базисе . Координаты точки
- •40 Скалярное произведение векторов свойства
- •2.Свойтсва скалярного произведения векторов.
- •43. Геометрический смысл скалярного, векторного и смешанного произведения.
- •Геометрические свойства векторного произведения
- •44.Аффинная система координат. Прямоугольная система координат?
- •45 Радиус Вектора Расстояние между двумя точками
- •46 Уравнение прямой на плоскости
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и направляющему вектору
- •47 Нормальный и направляющий вектор на прямой
- •48 Расположение двух прямых Условия параллельности и перпендикулярности прямых
- •49.Угол между двумя прямыми
- •50.Расстояние от точки до прямой
Теорема Кронекера — Капелли: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:
Количество главных переменных системы равно рангу системы.
Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
7 Системы линейных алгебраических уравнений? Метод Гауса?
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
|
Здесь — количество уравнений, а — количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].
Система линейных уравнений может быть представлена в матричной форме как:

или:
![]() .
.
Здесь
—
это матрица системы,
—
столбец неизвестных, а ![]() —
столбец свободных членов. Если к
матрице
приписать
справа столбец свободных членов, то
получившаяся матрица называется
расширенной.
—
столбец свободных членов. Если к
матрице
приписать
справа столбец свободных членов, то
получившаяся матрица называется
расширенной.
Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.
Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.
Система линейных алгебраических уравнений
![]() эквивалентна
системе
эквивалентна
системе
![]() ,
,
где — невырожденная матрица.
В
частности, если сама матрица
—
невырожденная, и для неё существует обратная
матрица ![]() ,
то решение системы уравнений можно
формально записать в виде
,
то решение системы уравнений можно
формально записать в виде
![]() .
.
Ме́тод Га́усса[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные[2].
Описание
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по
«ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Гаусса
требует порядка ![]() действий.
действий.
Этот Метод метод опирается на:
Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду.
Пример
Покажем, как методом Гаусса можно решить следующую систему:
![]()
Обнулим
коэффициенты при
во
второй и третьей строчках. Для этого
вычтем из них первую строчку, умноженную
на ![]() и
и ![]() ,
соответственно:
,
соответственно:
![]()
Теперь
обнулим коэффициент при
в
третьей строке, вычтя из неё вторую
строку, умноженную на ![]() :
:

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
![]() из
третьего;
из
третьего;
![]() из
второго, подставив полученное
из
второго, подставив полученное ![]()
![]() из
первого, подставив полученные
и
.
из
первого, подставив полученные
и
.
Таким образом исходная система решена.
Достоинства метода
Менее трудоёмкий по сравнению с другими методами.
Позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение.
Позволяет найти максимальное число линейно независимых уравнений — ранг матрицы системы[
8 Теорема Кронекера-Капелли
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных
Необходимость.Пусть система совместна.
Тогда существуют числа ![]() такие,
что
такие,
что ![]() .
Следовательно, столбец
является
линейной комбинацией столбцов
.
Следовательно, столбец
является
линейной комбинацией столбцов ![]() матрицы
.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что
матрицы
.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что ![]() .
.
Достаточность
Пусть ![]() .
Возьмем в матрице
какой-нибудь
базисный минор. Так как
.
Возьмем в матрице
какой-нибудь
базисный минор. Так как ![]() ,
то он же и будет базисным минором и
матрицы
.
Тогда согласно теореме о
базисном миноре последний
столбец матрицы
будет
линейной комбинацией базисных столбцов,
то есть столбцов матрицы
.
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы
.
,
то он же и будет базисным минором и
матрицы
.
Тогда согласно теореме о
базисном миноре последний
столбец матрицы
будет
линейной комбинацией базисных столбцов,
то есть столбцов матрицы
.
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы
.
Следствия
Количество главных переменных системы равно рангу системы.
Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
Решить с помощью теоремы Кронекера-Капелли систему уравнений:
 Решение
Решение
 Из последнего преобразования вытекает,
что
Из последнего преобразования вытекает,
что  .
Начальная система эквивалентна
системе:
.
Начальная система эквивалентна
системе:
 .
Среди миноров второго порядка,
составленных из элементов матрицы
коэффициентов при неизвестных, существует
хотя бы один отличный от нуля. В нашем
случае их несколько. Если отличный от
нуля минор выберем из коэффициентов
при двух неизвестных, то таким образом
мы переведем эти неизвестные в разряд
основных. Пусть, например, это неизвестные
х1,
х2.
Тогда, перенеся остальные неизвестные
в правую часть системы уравнений,
получим:
.
Среди миноров второго порядка,
составленных из элементов матрицы
коэффициентов при неизвестных, существует
хотя бы один отличный от нуля. В нашем
случае их несколько. Если отличный от
нуля минор выберем из коэффициентов
при двух неизвестных, то таким образом
мы переведем эти неизвестные в разряд
основных. Пусть, например, это неизвестные
х1,
х2.
Тогда, перенеся остальные неизвестные
в правую часть системы уравнений,
получим:
 .
Главный определитель этой системы
.
Главный определитель этой системы 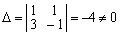 .
Найдем
.
Найдем  .
.
 .
По правилу Крамера
.
По правилу Крамера
 Последние равенства определяют общее
решение системы уравнений. Чтобы
получить частные решения, достаточно
предоставить свободным неизвестным
х3,
х4,
х5 некоторых
числовых значений.
Например, если
х3 =
0, х4 =
0, х5 =
0,
имеем решение
Последние равенства определяют общее
решение системы уравнений. Чтобы
получить частные решения, достаточно
предоставить свободным неизвестным
х3,
х4,
х5 некоторых
числовых значений.
Например, если
х3 =
0, х4 =
0, х5 =
0,
имеем решение  ;
если х3 =
2, х4 =
1, х5 =
–2 — решение (3, 5, 2, 1, –2) и т.д.
Таких частных решений в данном случае
можно построить бесконечное количество.
;
если х3 =
2, х4 =
1, х5 =
–2 — решение (3, 5, 2, 1, –2) и т.д.
Таких частных решений в данном случае
можно построить бесконечное количество.9 Определители. Свойства определителей?
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.
Определитель матрицы А обозначается как: det(A), |А| или Δ(A).
Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:
![]()
Для
матрицы ![]() детерминант
определяется как
детерминант
определяется как
![]()
Для
матрицы ![]() определитель
задаётся рекурсивно:
определитель
задаётся рекурсивно:
![]() ,
где
,
где ![]() — дополнительный
минор к
элементу
— дополнительный
минор к
элементу ![]() .
Эта формула называется разложением
по строке.
.
Эта формула называется разложением
по строке.
В
частности, формула вычисления определителя
матрицы ![]() такова:
такова:

![]()
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):
![]()
Свойства определителей
Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам):
 ,
где
,
где  и т. д. —
строчки матрицы,
и т. д. —
строчки матрицы,  —
определитель такой матрицы.
—
определитель такой матрицы.При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.
Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.
Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).
Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).
С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
![]()
10. Теорема о разложении определителей по строкам, по столбцам:
Теоре́ма Лапла́са — одна из теорем линейной алгебры. Названа в честь французского математика Пьера-Симона Лапласа (1749 — 1827), которому приписывают создание этой теоремы в 1772 году[1], хотя частный случай этой теоремы о разложении определителя по строке (столбцу) был известен ещё Лейбницу.
Формулировка
Для начала, введём несколько определений.
Пусть ![]() — матрица размера
,
и пусть выбраны любые
строк
матрицы
с
номерами
— матрица размера
,
и пусть выбраны любые
строк
матрицы
с
номерами ![]() и
любые
столбцов
с номерами
и
любые
столбцов
с номерами ![]() .
.
Определитель матрицы,
получаемой из
вычеркиванием
всех строк и столбцов, кроме выбранных,
называется минором
-го
порядка, расположенным в строках с
номерами ![]() и
столбцах с номерами
и
столбцах с номерами ![]() .
Он обозначается следующим образом:
.
Он обозначается следующим образом:

А
определитель матрицы, получаемой
вычеркиванием только выбранных строк
и столбцов из квадратной матрицы,
называется дополнительным
минором к
минору ![]() :
:

где ![]() и
и ![]() —
номера невыбранных строк и стобцов.
—
номера невыбранных строк и стобцов.
Алгебраическое дополнение минора определяется следующим образом:
![]()
где ![]() ,
, ![]() .
.
Справедливо следующее утверждение.
Теорема Лапласа
Пусть выбраны любые строк матрицы . Тогда определитель матрицы равен сумме всевозможных произведений миноров -го порядка, расположенных в этих строках, на их алгебраические дополнения.
![]()
где
суммирование ведётся по всевозможным
номерам столбцов ![]()
Число
миноров, по которым берётся сумма в
теореме Лапласа, равно числу способов
выбрать
столбцов
из
,
то есть биномиальному
коэффициенту ![]() .
.
Так как строки и столбцы матрицы равносильны относительно свойств определителя, теорему Лапласа можно сформулировать и для столбцов матрицы.
Разложение определителя по строке (столбцу) (Следствие 1)
Широко известен частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения.
Пусть
—
квадратная матрица размера
.
Пусть также задан некоторый номер
строки ![]() либо
номер столбца
либо
номер столбца ![]() матрицы
.
Тогда определитель
может
быть вычислен по следующим формулам:
матрицы
.
Тогда определитель
может
быть вычислен по следующим формулам:
Разложение по -й строке:

Разложение по -му столбцу:
![]()
где ![]() —
алгебраическое дополнение к минору,
расположенному в строке с номером
и
столбце с номером
.
также
называют алгебраическим дополнением
к элементу
—
алгебраическое дополнение к минору,
расположенному в строке с номером
и
столбце с номером
.
также
называют алгебраическим дополнением
к элементу ![]() .
.
Утверждение является частным случаем теоремы Лапласа. Достаточно в ней положить равным 1 и выбрать -ую строку, тогда минорами, расположенными в этой строке будут сами элементы.
Следствие 2 (фальшивое разложение определителя)
Сумма произведений всех элементов некоторой строки (столбца) матрицы А на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю.
Доказательство. Рассмотрим сумму произведений всех элементов произвольной k-ой строки матрицы А на алгебраические дополнения соответствующих элементов любой другой, скажем, i-ой строки матрицы А. Пусть A′ – матрица, у которой все строки, кроме i-ой, такие же, как у матрицы А, а элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матрицы А. Тогда у матрицы A′ две одинаковые строки и, следовательно, по свойству матрицы об одинаковых строках имеем, что |A′| = 0 . С другой стороны, по следствию 1 определитель |A′| равен сумме произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения. Заметим, что алгебраические дополнения элементов i-ой строки матрицы A′ совпадают с алгебраическими дополнениями соответствующих элементов i-ой строки матрицы А. Но элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матри- цы А. Таким образом, сумма произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения с одной стороны равна нулю, а с другой стороны равна сумме произведений всех элементов k-ой строки матрицы А на алгебраические дополнения соответствующих элементов i-ой строки матрицы А
11. Теорема Крамера
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.
Описание метода
Для системы линейных уравнений с неизвестными (над произвольным полем)

с
определителем матрицы системы ![]() ,
отличным от нуля, решение записывается
в виде
,
отличным от нуля, решение записывается
в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:

В
этой форме формула Крамера справедлива
без предположения, что
отлично
от нуля, не нужно даже, чтобы коэффициенты
системы были бы элементами целостного
кольца (определитель
системы может быть даже делителем нуля
в кольце коэффициентов). Можно также
считать, что либо наборы ![]() и
и ![]() ,
либо набор
,
либо набор ![]() состоят
не из элементов кольца коэффициентов
системы, а какого-нибудь модуля над
этим кольцом. В этом виде формула Крамера
используется, например, при доказательстве
формулы для определителя
Грама и Леммы
Накаямы.
состоят
не из элементов кольца коэффициентов
системы, а какого-нибудь модуля над
этим кольцом. В этом виде формула Крамера
используется, например, при доказательстве
формулы для определителя
Грама и Леммы
Накаямы.
Пример
Система линейных уравнений:
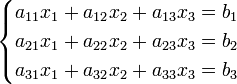
Определители:


Решение:
![]()
Пример:

Определители:


![]()
Вычислительная сложность
Метод
Крамера требует вычисления ![]() определителей
размерности
.
При использовании метода
Гаусса для
вычисления определителей, метод имеет
временную сложность порядка
определителей
размерности
.
При использовании метода
Гаусса для
вычисления определителей, метод имеет
временную сложность порядка ![]() ,
что хуже, чем если бы метод
Гаусса напрямую
использовался для решения системы
уравнений. Поэтому метод считался
непрактичным. Однако в 2010 году было
показано, что метод Крамера может быть
реализован со сложностью
,
сравнимой со сложностью метода
Гаусса.
,
что хуже, чем если бы метод
Гаусса напрямую
использовался для решения системы
уравнений. Поэтому метод считался
непрактичным. Однако в 2010 году было
показано, что метод Крамера может быть
реализован со сложностью
,
сравнимой со сложностью метода
Гаусса.
12. Теорема о определителях произведении матриц?
Теорема. Определитель произведения двух матриц п-го порядка равен произведению определителей этих матриц.
Пусть
даны матрицы п-го
порядка
 и
и
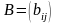 и пусть
и пусть
 .
Построим определитель
порядка 2п:
в его верхнем левом углу поставим матрицу
А,
в правом нижнем – матрицу В,
в правом верхнем углу поставим нули, а
на главной диагонали левого нижнего
угла поставим числа –1, заполнив свободные
места нулями. Определитель
будет иметь вид
.
Построим определитель
порядка 2п:
в его верхнем левом углу поставим матрицу
А,
в правом нижнем – матрицу В,
в правом верхнем углу поставим нули, а
на главной диагонали левого нижнего
угла поставим числа –1, заполнив свободные
места нулями. Определитель
будет иметь вид

Применим к определителю D теорему Лапласа о разложении по первым п строкам. В результате получим
D = detAdetB
Преобразуем
определитель D
так, чтобы при неизменности его значения
все элементы bij
стали
нулями. Для этого к п+1-му
столбцу прибавим первый столбец,
умноженный на b11,
второй столбец, умноженный на b21
и т. д. К (п + 2)му
столбцу прибавим первый, умноженный на
b12,
второй, умноженный на
b22
и
т. д.
Вообще к (n + j)-столбцу,
где j =1,2,,п,
прибавим сумму первых п
столбцов, умноженных соответственно
на
 .
.
Такие
преобразования привели к тому, что в
правом нижнем углу определителя (будем
называть его по-прежнему D,
так как величина его не изменилась)
оказались только нули. В правом верхнем
углу определителя теперь появятся
числа, определённые следующим образом:
в i-той
строке в столбце с номером n + j
будет стоять сумма
 .
Эта сумма, исходя из правила перемножения
матриц, равна элементу матрицы
.
Эта сумма, исходя из правила перемножения
матриц, равна элементу матрицы
 .
Таким образом, в правом верхнем углу
оказалась матрица С.
Определитель D
принял вид
.
Таким образом, в правом верхнем углу
оказалась матрица С.
Определитель D
принял вид

Применим теперь разложение определителя по последним п столбцам. Дополнительный минор для минора, стоящего на пересечении первых п строк и последних п столбцов равен (–1)п. Для самого минора сумма s, определяемая формулой (*), будет равна

Отсюда получается:

13. Теорема о нахождении обратной матрицы с помощью алгебраической дополнении
Рассмотрим квадратную матрицу
 .
.
Обозначим =det A.
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если = 0.
Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.
Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Матрица, обратная матрице А, обозначается через А1, так что В = А1. Обратная матрица вычисляется по формуле
 ,
(4.5)
,
(4.5)
где А i j - алгебраические дополнения элементов a i j.
Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ранга матрицы можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример
2.10.
Для матрицы  найти
обратную.
найти
обратную.
Решение. Находим
сначала детерминант матрицы А

значит, обратная матрица существует и мы ее можем найти по формуле:
 ,
,
где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Откуда
 .
.
14. Нахождение обратной матрицы с помощью элементарной преобразовании
предположим, что матрица A - неособенная и рассмотрим метод нахождения обратной матрицы, основанный на элементарных операциях над строками.
В данном контексте под элементарными преобразованиями понимается:
Умножение строки на любое ненулевое число.
Прибавление к одной строке любой другой, предварительно умноженной на любое число.
Алгоритм метода чрезвычайно прост по своей сути.
Сначала составляется расширенная матрица – присоединением к матрице A единичной матрицы E:

Затем с помощью элементарных операций над строками расширенная матрица (A | E) преобразуется к виду (E | B). С формальной точки зрения такие преобразования могут быть реализованы умножением на матрицу A некоторой матрицы T, которая представляет собой произведение соответствующих элементарных матриц (матрицы перестановки, матрицы масштабирования, неунитарной матрицы):
TA = E.
Это уравнение означает, что матрица преобразования T представляет собой обратную матрицу для матрицы A:
T = A-1.
Тогда TE = A-1 и, следовательно,
![]()
15. Поле комплексных чисел. Алгебраическая формула комплексных чисел
Ко́мпле́ксные[1] чи́сла (устар. Мнимые
числа[2]),
— расширение множества вещественных
чисел,
обычно обозначается ![]() .
Любое комплексное число может быть
представлено как формальная сумма
.
Любое комплексное число может быть
представлено как формальная сумма ![]() ,
где
и
—
вещественные числа,
— мнимая
единица[3].
,
где
и
—
вещественные числа,
— мнимая
единица[3].
Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени с комплексными коэффициентами имеет ровно комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике, гидродинамике, картографии,квантовой механике, теории колебаний и многих других.
Поле
комплексных чисел можно понимать
как расширение
поля вещественных
чисел, в котором многочлен ![]() имеет
корень. Следующие две
элементарные модели показывают,
что непротиворечивое построение такой
системы чисел возможно. Оба приведенных
определения приводят к изоморфным расширениям
поля вещественных чисел
имеет
корень. Следующие две
элементарные модели показывают,
что непротиворечивое построение такой
системы чисел возможно. Оба приведенных
определения приводят к изоморфным расширениям
поля вещественных чисел ![]() ,
как и любые другие конструкции поля
разложения многочлена
.
,
как и любые другие конструкции поля
разложения многочлена
.
Стандартная модель
Комплексное
число
можно определить как упорядоченную
пару вещественных чисел
![]() .
Введём операции сложения и умножения
таких пар следующим образом:
.
Введём операции сложения и умножения
таких пар следующим образом:
![]()
![]()
Алгебраическая форма
Запись
комплексного числа
в
виде
, ![]() ,
называется алгебраической
формой комплексного
числа.
,
называется алгебраической
формой комплексного
числа.
Сумма
и произведение комплексных чисел могут
быть вычислены непосредственным
суммированием и перемножением таких
выражений, как обычно раскрывая скобки
и приводя подобные, чтобы представить
результат тоже в стандартной форме (при
этом надо учесть, что ![]() ):
):
![]()
![]()
Алгебраическое
расширение поля действительных чисел ![]() с
помощью элемента
с
помощью элемента ![]() ,
являющегося корнем
многочлена
,
являющегося корнем
многочлена ![]() ,
называется полем комплексных чисел1). Поле комплексных чисел обозначается
через
,
называется полем комплексных чисел1). Поле комплексных чисел обозначается
через ![]() .
.
Предложение
1. Каждое ассоциативное
коммутативное кольцо ![]() с
единицей и
без делителей
нуля,
являющееся двумерным векторным
пространством над
полем
,
изоморфно полю
.
с
единицей и
без делителей
нуля,
являющееся двумерным векторным
пространством над
полем
,
изоморфно полю
.
Теорема 1.(Основная теорема алгебры.) Поле комплексных чисел алгебраически замкнуто.
16.Тригонометрическая форма комплексных
![]()
где r -
модуль; ![]() -
агрумент комплексного числа.
-
агрумент комплексного числа.
Если ![]() то:
то:
![]()
![]()
![]()
![]()
Формула Муавра
![]()
Извлечение корней из комплексных чисел
![]()
![]()
Та
запись комплексного числа, которую мы
использовали до сих пор,
называется алгебраической
формой записи комплексного числа.
Часто бывает удобна немного другая
форма записи комплексного числа.
Пусть ![]() и
φ = arg z.
Тогда по определению аргумента имеем:
и
φ = arg z.
Тогда по определению аргумента имеем:
|
Отсюда получается
z = a + bi = r(cos φ + i sin φ). |
Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.
17. Умножение и деление комплексного числа в тригонометрической форме?
п.2. Деление комплексных чисел в тригонометрической форме записи.
Теорема. (О делении комплексных чисел в тригонометрической форме)
Пусть ![]() ,
где
,
где ![]() и
и ![]() ,
где
,
где ![]() –
два произвольных комплексных числа записанных
в тригонометрической форме. Тогда
–
два произвольных комплексных числа записанных
в тригонометрической форме. Тогда
![]() .
(2)
.
(2)
Доказательство. Воспользуемся следствием формулы Муавра и правилом умножения комплексных чисел в тригонометрической форме записи. Получаем:
![]()
![]()
![]() ,
ч.т.д.
,
ч.т.д.
Пример
1. Запишите комплексные числа ![]() и
и ![]() в
тригонометрической форме и найдите
их произведение
в
тригонометрической форме и найдите
их произведение ![]() и
частное
и
частное ![]() .
.
Решение. 1) Комплексное число на комплексной плоскостинаходится во второй четверти, поэтому
![]() ,
, ![]() .
.
2) Комплексное число на комплексной плоскости находится во четвертой четверти, поэтому
![]() ,
, ![]() .
.
3) ![]()
![]() .
.
![]() Ответ:
Ответ: ![]() ,
, ![]() .
.
Пример
2. Вычислить ![]() .
.
Решение.
Комплексное число ![]() на комплексной плоскостинаходится
в третьей четверти, поэтому
на комплексной плоскостинаходится
в третьей четверти, поэтому ![]() ,
, ![]()
Применим формулу Муавра:
![]()
![]()
![]()
![]() .
.
Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.)
Пусть
,
где
и ![]() ,
где
–
два произвольных комплексных числа записанных
в тригонометрической форме. Тогда
,
где
–
два произвольных комплексных числа записанных
в тригонометрической форме. Тогда
![]() .
(13)
.
(13)
Доказательство. ![]()
![]()
![]()
![]() ,
ч.т.д.
,
ч.т.д.
Теорема доказана.
Отсюда вытекает правило умножения комплексных чисел в тригонометрической форме записи.
Для того, чтобы перемножить два комплексных числа в тригонометрической форме записи нужно перемножить их модули, а аргументы сложить.
Следствие
1. Пусть k натуральное число и ![]() .
Пусть далее
.
Пусть далее ![]() ,
где
,
где ![]() –
произвольные n комплексных чисел
записанных в тригонометрической форме
записи. Тогда
–
произвольные n комплексных чисел
записанных в тригонометрической форме
записи. Тогда
![]()
![]() .
.
Доказательство проводится индукцией по числу сомножителей и предоставляется читателю.
Следствие
2. Пусть n натуральное число и ![]() –
произвольное комплексное число в
тригонометрической форме записи. Тогда
–
произвольное комплексное число в
тригонометрической форме записи. Тогда
![]() .
.
Доказательство сразу же следует из Следствия 1.
18. Нахождения корня комплексного числа в тригонометрической форме?
Формула
(6) для произведения двух комплексных
чисел может быть обобщена на случай
 сомножителей.
Используя метод математической индукции,
нетрудно показать, что если
сомножителей.
Используя метод математической индукции,
нетрудно показать, что если
 -аргументы
чисел
-аргументы
чисел
 соответственно,
то
соответственно,
то

Отсюда,
как частный случай, получается формула,
дающая правило возведение комплексного
числа
 в целую положительную степень:
в целую положительную степень:
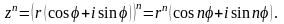 (8)
(8)
Таким образом, при возведении комплексного числа в степень с натуральным показателем его модуль возводится в степень с тем же показателем, а аргумент умножается на показатель степени.
Формула (8) называется формулой Муавра.
Число
 называется
корнем степени
,
называется
корнем степени
, из числа обозначается
из числа обозначается
 ,если
,если

Если
=0,
то при любом n
уравнение
 имеет
одно и только одно решение z=0.
имеет
одно и только одно решение z=0.
Пусть
теперь
 .Представим
z
и
в тригонометрической форме:
.Представим
z
и
в тригонометрической форме:
 ,
,
 .
.
Тогда
уравнение
 примет вид
примет вид

Два комплексных числа равны тогда и только тогда, когда равны их модули, а аргументы отличаются на число, кратное 2. Следовательно,

или
 .
.
Таким образом, все решения уравнения даются формулой

В
самом деле, придавая числу k
в
формуле (9)целые значения, отличные от
0, 1, …, (n-1),
мы не получаем других комплексных
чисел.Формула (9) называется второй
формулой Муавра.Таким
образом, если
,
то существует ровно n
корней степени n
из числа :
все они содержатся в формуле(9).В частности,
если
=2,
то уравнение
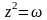 имеет два корня:
имеет два корня:

то
есть эти корни симметричны относительно
начала координат.Также из формулы (9)
нетрудно получить, что если то
точки, изображающие все корни уравнения
,
являются вершинами правильного
n-угольника,
вписанного в
то
точки, изображающие все корни уравнения
,
являются вершинами правильного
n-угольника,
вписанного в
окружность
с центром в точке z=0
и радиусом
 .Из
сказанного выше следует, что символ
не
имеет однозначного смысла. Поэтому,
употребляя его, следует четко представлять
себе, что под этим подразумевается.
Например,
.Из
сказанного выше следует, что символ
не
имеет однозначного смысла. Поэтому,
употребляя его, следует четко представлять
себе, что под этим подразумевается.
Например,
используя
запись
 ,
следует позаботиться о том, чтобы было
ясно, понимается ли под этим пара
комплексных чисел i
и-i,или
одно, и, если одно, то какое именно.
,
следует позаботиться о том, чтобы было
ясно, понимается ли под этим пара
комплексных чисел i
и-i,или
одно, и, если одно, то какое именно.
19. Корни из единицы п-ой степени?


20. Кольцо многочленов. Операции над многочленами?
Обозначим через K(x) множество многочленов с коэффициентами из кольца K. На множестве этих многочленов можно определить операции сложения и умножения многочленов. Кольцо многочленов коммутативно если исходное кольцо коммутативно.
Операции над многочленами.
Два
полинома считаются равными,
если они составлены в канонической
записи из одинаковых одночленов, т.е.
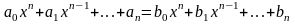 в том и только в том случае, если
в том и только в том случае, если
 .Суммой
двух полиномов называется полином,
получающийся посредством объединения
одночленов, составляющих слагаемые.
Разумеется, после объединения следует
привести подобные члены. Таким образом,
.Суммой
двух полиномов называется полином,
получающийся посредством объединения
одночленов, составляющих слагаемые.
Разумеется, после объединения следует
привести подобные члены. Таким образом,


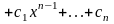 ,
где
,
где
 .
(Если многочлены f(x)
и g(x)
имеют разное число одночленов, то,
подписав необходимое число одночленов
с нулевыми коэффициентами к одному из
них, в котором число одночленов меньше,
можно добиться их равенства в обоих
многочленах). Поэтому складывать можно
многочлены с разным числом одночленов.
Например,
.
(Если многочлены f(x)
и g(x)
имеют разное число одночленов, то,
подписав необходимое число одночленов
с нулевыми коэффициентами к одному из
них, в котором число одночленов меньше,
можно добиться их равенства в обоих
многочленах). Поэтому складывать можно
многочлены с разным числом одночленов.
Например,
 ,
,
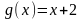 ,
преобразуем g(x)
к виду
,
преобразуем g(x)
к виду
 добавив два нулевых одночлена, суммой
f(x)
и g(x)
будет многочлен
добавив два нулевых одночлена, суммой
f(x)
и g(x)
будет многочлен

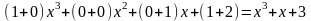 )
Из соотношения
)
Из соотношения
(1)
легко
видеть, что операция суммирования
(сложения) многочленов обладает такими
же свойствами, что и операция сложения
элементов кольца K,
т.е. ассоциативна, коммутативна; полином,
все коэффициенты которого нули, является
нейтральным элементом сложения полиномов;
для каждого полинома существует ему
противоположный, противоположный к
полиному
 является полином
является полином
 .
Итак, множество полиномов с операцией
сложения образует коммутативную группу.
.
Итак, множество полиномов с операцией
сложения образует коммутативную группу.
Произведением
двух полиномов называется полином,
составленный из произведений всех
членов первого сомножителя на все члены
второго. Здесь снова возможно приведение
подобных членов. Таким образом,

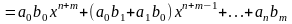 .
Коэффициент
.
Коэффициент
 при
при
 равен
равен
 ,
если условиться считать, что
,
если условиться считать, что
 при
при
 и
и
 при
при
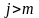 .
Принцип вычисления коэффициента
прост: приводятся такие подобные
слагаемые при произведении одночленов
.
Принцип вычисления коэффициента
прост: приводятся такие подобные
слагаемые при произведении одночленов
 и
и
 ,
которые дают в результате одночлены
вида
,
которые дают в результате одночлены
вида
 ,
т.е.
-
сумма всевозможных произведений
,
т.е.
-
сумма всевозможных произведений
 и
и
 при
при
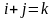 .
Поэтому верно равенство
.
Поэтому верно равенство
 .
(2)
.
(2)
Умножение
многочленов ассоциативно.
Это доказывается следующим образом:
если помимо многочленов
 и
и
 дан еще многочлен
дан еще многочлен
 ,
,
 ,
то коэффициентом при
,
то коэффициентом при
 ,
,
 в произведении
в произведении
 будет служить элемент
будет служить элемент
 ,
а в произведении
,
а в произведении
 - равное ему число
- равное ему число
 .
.
Умножение
многочленов дистрибутивно
относительно сложения, это вытекает из
равенства
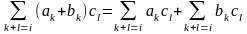 ,
так как левая часть этого равенства
является коэффициентом при
в многочлене
,
так как левая часть этого равенства
является коэффициентом при
в многочлене
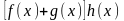 ,
а правая часть - коэффициентом при той
же степени переменной
,
а правая часть - коэффициентом при той
же степени переменной
 в многочлене
в многочлене
 .
.
Нетрудно
видеть, что многочлен
 (где 1 - единица кольца K)
играет роль единицы при умножении
многочленов. Таким образом, множество
полиномов от буквы x
с коэффициентами из кольца составляет
кольцо по отношению к выше определенным
операциям сложения и умножения полиномов
(относительно сложения - это коммутативная
группа; умножение ассоциативно и
дистрибутивно относительно сложения;
существует единичный многочлен). Кольцо
это коммутативно и ассоциативно. Оно
называется кольцом
полиномов
от буквы x
над кольцом K
и обозначается K[x].
(где 1 - единица кольца K)
играет роль единицы при умножении
многочленов. Таким образом, множество
полиномов от буквы x
с коэффициентами из кольца составляет
кольцо по отношению к выше определенным
операциям сложения и умножения полиномов
(относительно сложения - это коммутативная
группа; умножение ассоциативно и
дистрибутивно относительно сложения;
существует единичный многочлен). Кольцо
это коммутативно и ассоциативно. Оно
называется кольцом
полиномов
от буквы x
над кольцом K
и обозначается K[x].
В
данном выше определении одночлена и
полинома имеется одно сомнительное
место. Именно, было сказано, что x
есть буква, посторонняя для кольца K,
и не было объяснено, что это значит.
Сказать, что x
не принадлежит кольцу K
- это сказать слишком мало, так как при
этом не исключаются нежелательные
возможности
 или
или
 и т.д. Однако мы можем избавиться от
"сомнительной" буквы x.
Для этого рассмотрим бесконечные
последовательности
и т.д. Однако мы можем избавиться от
"сомнительной" буквы x.
Для этого рассмотрим бесконечные
последовательности
 элементов кольца K,
в которых все элементы, начиная с
некоторого, равны нулю. Вводим теперь
определения равенства и основных
действий.
элементов кольца K,
в которых все элементы, начиная с
некоторого, равны нулю. Вводим теперь
определения равенства и основных
действий.
 тогда
и только тогда, когда
тогда
и только тогда, когда
 ,
i
= 0, 1, ..., k,
...
,
i
= 0, 1, ..., k,
... .
Ясно, что требование об обращении в
нуль всех членов, начиная с некоторого,
сохраняется при сложении.
.
Ясно, что требование об обращении в
нуль всех членов, начиная с некоторого,
сохраняется при сложении. .
Здесь тоже сохраняется требование об
обращении в нуль всех членов, начиная
с некоторого места.
.
Здесь тоже сохраняется требование об
обращении в нуль всех членов, начиная
с некоторого места.
Легко
проверяется коммутативность и
ассоциативность сложения и умножения
и дистрибутивность умножения со
сложением. Далее ясно, что

 и
и
 ,
и, более общо,
,
и, более общо,
 .
.
4.
 отождествляется с последовательностью
отождествляется с последовательностью
 .
.
Рассмотрим
теперь последовательность (0, 1, 0, ..., 0,
...), обозначив ее буквой x.
Тогда x2
= (0, 0, 1, 0, ..., 0, ...) и т.д. Поэтому




 .
Таким образом, мы построили элементы
кольца K[x]
полиномов.
.
Таким образом, мы построили элементы
кольца K[x]
полиномов.
Итак, при определении многочлена
(3)
существенны
лишь коэффициенты
 ,
и поэтому можно было бы писать вместо
(1) последовательность
,
и поэтому можно было бы писать вместо
(1) последовательность
 .
Однако, в конечном счете, запись многочлена
в виде выражения (3) оказывается более
удобной.
.
Однако, в конечном счете, запись многочлена
в виде выражения (3) оказывается более
удобной.
Пусть
,
причем
 .
Одночлен
.
Одночлен
 называется высшим
(старшим)
членом
полинома f(x)
и показатель n
называется степенью
f(x)
и обозначается deg
f.
Нулевой полином не имеет высшего члена
в смысле данного определения и считается,
что он равен нулю. Коэффициент
называется высшим
(старшим)
членом
полинома f(x)
и показатель n
называется степенью
f(x)
и обозначается deg
f.
Нулевой полином не имеет высшего члена
в смысле данного определения и считается,
что он равен нулю. Коэффициент
 называется свободным
членом.
Многочлен, старший коэффициент которого
равен единице, называется нормированным.При
сложениимногочленов
и
по формуле (1) мы видим, что формула для
суммы не содержит членов, степень которых
выше, чем
называется свободным
членом.
Многочлен, старший коэффициент которого
равен единице, называется нормированным.При
сложениимногочленов
и
по формуле (1) мы видим, что формула для
суммы не содержит членов, степень которых
выше, чем
 ,
а формула для произведения - членов,
степень которых выше, чем n
+ m.
,
а формула для произведения - членов,
степень которых выше, чем n
+ m.
21. Деление с остатком в кольце многочленов?
Теорема
1.13.8 (алгоритм деления с остатком в кольце
многочленов). Для любых многочленов
![]() ,
,
![]() ,
существуют (и притом единственные)
многочлены
,
существуют (и притом единственные)
многочлены
![]() такие, что:
такие, что:
1)f(x)=g(x)q(x)+r(x) ;
2)либо
r(x)=0, либо
![]() ,
,
![]() .
.
Доказательство-алгоритм (деление многочленов столбиком).
Пусть
f(x) = anxn+...+a1x+a0, g(x) = bsxs+...+b1x+b0,
![]() .
.
Если n<s, то утверждение 1) очевидно:
![]()
Пусть
![]() .
Тогда:
.
Тогда:

Складывая все эти равенства и сокращая, получаем

т. е. f(x)=q(x)g(x)+r(x), где

Если
f(x)=g(x)q(x)+r(x)=g(x)q'(x)+r'(x),
при этом r(x),r'(x)
или равны нулю, или имеют степень, меньшую
чем
![]() ,
то g(x)(q(x)-q'(x))=r'(x)-r(x).
Если
,
то g(x)(q(x)-q'(x))=r'(x)-r(x).
Если
![]() ,
то получаем противоречие, поскольку
степень левой части
,
то получаем противоречие, поскольку
степень левой части
![]() ,
а многочлен в правой части или нулевой,
или его степень
,
а многочлен в правой части или нулевой,
или его степень
![]() .
Итак, q(x)=q'(x),
и поэтому r'(x)=r(x).
.
Итак, q(x)=q'(x),
и поэтому r'(x)=r(x).
Замечание
1.13.9. Если K
- подполе поля K'
(например,
![]() ),
),
![]() ,
f(x)=g(x)q(x)+r(x)
- деление с остатком в кольце многочленов
K'[x],
то
.
,
f(x)=g(x)q(x)+r(x)
- деление с остатком в кольце многочленов
K'[x],
то
.
22. Алгоритм Евклида в кольце многочленов?
Алгори́тм Евкли́да — алгоритм для нахождения наибольшего общего делителя двух целых чисел.Кольца, в которых применим алгоритм Евклида, называются евклидовыми кольцами. К ним относятся, в частности, кольца многочленов.Обобщённый алгоритм Евклида для многочленов.Алгоритм Евклида и расширенный алгоритм Евклида естественным образом обобщается на кольцо многочленов k[x] от одной переменной над произвольным полем k, поскольку для таких многочленов определена операция деления с остатком. При выполнении алгоритма Евклида для многочленов аналогично алгоритму Евклида для целых чисел, получается последовательность полиномиальных остатков (PRS).
Пример для кольца Z[x].Пусть cont(f) по определению — НОД коэффициентов многочлена f(x) из Z[x] — содержание многочлена. Частное от деления f(x) на cont(f) называется примитивной частью многочлена f(x) и обозначается primpart(f(x)).эти определения понадобятся для нахождения НОД двух многочленов p1(x) и p2(x) в кольце Z[x]. Для многочленов над целыми числами верно следующее:
![]() НОД
НОД
![]() НОД
НОД
![]() ,
,
![]() НОД
НОД
НОД
НОД![]() .
.
Таким образом задача отыскания НОД двух произвольных многочленов сводится к задаче отыскания НОД примитивных полиномов.Пусть есть два примитивных многочлена p1(x) и p2(x) из Z[x], для которых выполняется соотношение между их степенями: deg(p1(x)) = m и deg(p2(x)) = n, m > n. Деление многочленов с остатком предполагает точную делимость старшего коэффициента делимого на старший коэффициент делителя, в общем случае деление с остатком выполнить невозможно. Поэтому вводят алгоритм псевдоделения, который всё же позволяет получить
псевдочастное и псевдоостаток (prem), которые будут сами по себе принадлежать множеству многочленов над целыми числами.
23. Нод и нок двух многочленов?
Наибольший общий делитель двух многочленов Наибольший общий делитель многочленов f(x) и g(x) - такой их общий делитель d(x), который делится на любой другой их общий делитель.Алгоритм Евклида (алгоритм последовательного деления) нахождения наибольшего общего делителя многочленов f(x) и g(x)

Тогда
![]() - наибольший общий делитель f(x)
и g(x).Пусть
cont(f)
по определению — НОД коэффициентов
многочлена f(x)
из Z[x]
— содержание многочлена. Частное от
деления f(x)
на cont(f)
называется примитивной частью многочлена
f(x)
и обозначается primpart(f(x)).эти
определения понадобятся для нахождения
НОД двух многочленов p1(x)
и p2(x)
в кольце Z[x].
Для многочленов над целыми числами
верно следующее:
- наибольший общий делитель f(x)
и g(x).Пусть
cont(f)
по определению — НОД коэффициентов
многочлена f(x)
из Z[x]
— содержание многочлена. Частное от
деления f(x)
на cont(f)
называется примитивной частью многочлена
f(x)
и обозначается primpart(f(x)).эти
определения понадобятся для нахождения
НОД двух многочленов p1(x)
и p2(x)
в кольце Z[x].
Для многочленов над целыми числами
верно следующее:
НОД НОД , НОД НОД .
Таким
образом задача отыскания НОД двух
произвольных многочленов сводится к
задаче отыскания НОД примитивных
полиномов.Пусть есть два примитивных
многочлена p1(x)
и p2(x)
из Z[x],
для которых выполняется соотношение
между их степенями: deg(p1(x))
= m
и deg(p2(x))
= n,
m
> n.
Деление многочленов с остатком
предполагает точную делимость старшего
коэффициента делимого на старший
коэффициент делителя, в общем случае
деление с остатком выполнить невозможно.
Поэтому вводят алгоритм псевдоделения,
который всё же позволяет получить
псевдочастное и псевдоостаток (prem),
которые будут сами по себе принадлежать
множеству многочленов над целыми
числами.Под псевдоделением будем
понимать, что самому делению предшествует
умножение полинома p1(x) на ,
![]() то есть
то есть
![]() ,
,
![]() ,
где
,
где
![]() и
и
![]() —
соответственно псевдочастное и
псевдоостаток.
—
соответственно псевдочастное и
псевдоостаток.
Итак,
![]() — (принадлежат кольцу многочленов над
целыми числами), причём
— (принадлежат кольцу многочленов над
целыми числами), причём
![]() .
Тогда алгоритм Евклида состоит из
следующих шагов:
.
Тогда алгоритм Евклида состоит из
следующих шагов:
1. Вычисление НОД содержаний:
НОД
 .
.
2. Вычисление примитивных частей:
![]()
![]() .
.
3. Построение последовательности полиномиальных остатков:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4. Выход и возврат результата:
Если
![]() ,
то вернуть c,
иначе вернуть
,
то вернуть c,
иначе вернуть
![]() .
.
Наименьшее общее кратное (НОК) двух целых чисел m и n — это наименьшее натуральное число, которое делится на m и n. Обозначается НОК(m,n) или , а в английской литературе lcm(m,n).
24. Корни многочленов. Простые и кратные формы?
Рассмотрим в комплексной области многочлен, то есть функцию вида , (8.1)
где - комплексные числа. Числа называются коэффициентами многочлена, а натуральное число n — его степенью.
Определение 8.1. Два многочлена Pn (z) и равны тогда и только тогда, когда m=n, a0 = b0 , a1 = b1 ,…, an = bn .
Определение 8.2. Число z0 называется корнем многочлена (8.1), если Pn (z0) = 0.
Теорема 8.1 (теорема Безу). Остаток от деления многочлена Pn(z) на z — z0 ( z0 — не обязательно корень многочлена) равен P(z0).
Доказательство. Разделив P(z) на z — z0 , получим: P(z) = Q(z)(z — z0) + r, где число r — остаток от деления, а Q(z) — многочлен степени, меньшей n. При подстановке в это равенство z = z0 найдем, что r = P(z0), что и требовалось доказать.
Теорема 8.2 (основная теорема алгебры). Всякий многочлен в комплексной области имеет корень (без доказательства).
Разложение многочлена в комплексной области на линейные множители.
Пусть Pn (z) — многочлен степени n, а z1 — его корень. Тогда по теореме Безу Pn (z) можно представить в виде:
Pn (z) = (z — z1) Qn-1 (z),
где Qn-1 — многочлен степени n — 1. Если при этом Qn-1 (z1) = 0, его вновь можно представить как ( z — z1 )Qn-2 (z), a Pn (z) = (z — z1)Qn-2 (z).
Определение 8.3. Натуральное число k1 называется кратностью корня z1 многочлена Pn (z), если этот многочлен делится на , но не делится на . Корень кратности 1 называется простым, а корень кратности, большей 1, - кратным.
Итак, если z1 — корень Pn кратности k1 , то Из основной теоремы алгебры следует, что многочлен тоже имеет корень. Обозначим его z2 , а его кратность k2 . Тогда а , (8.2)
где Следовательно, в комплексной области всякий многочлен можно разложить на линейные множители.Корень многочлена (не равного тождественно нулю)
![]()
над
полем k
— элемент
![]() ,
такой что выполняются два следующих
равносильных условия:данный многочлен
делится на многочлен
,
такой что выполняются два следующих
равносильных условия:данный многочлен
делится на многочлен
![]() ;подстановка
элемента c
вместо x
обращает уравнение
;подстановка
элемента c
вместо x
обращает уравнение
![]() в тождество.
в тождество.
Равносильность двух формулировок следует из теоремы Безу. В различных источниках любая одна из двух формулировок выбирается в качестве определения, а другая выводится в качестве теоремы.
Свойства
Число
корней многочлена степени n
не превышает n
даже в том случае, если кратные корни
учитывать кратное количество раз.Всякий
многочлен
![]() с комплексными коэффициентами имеет
по крайней мере один, вообще говоря,
комплексный, корень (основная теорема
алгебры) . Аналогичное утверждение верно
для любого алгебраически замкнутого
поля (по определению).Более того, многочлен
с вещественными коэффициентами
можно записать в виде
с комплексными коэффициентами имеет
по крайней мере один, вообще говоря,
комплексный, корень (основная теорема
алгебры) . Аналогичное утверждение верно
для любого алгебраически замкнутого
поля (по определению).Более того, многочлен
с вещественными коэффициентами
можно записать в виде
![]() где
где
![]() — (в общем случае комплексные) корни
многочлена
,
возможно с повторениями, при этом если
среди корней
многочлена
встречаются равные, то общее их значение
называется кратным корнем.Число
комплексных корней многочлена с
комплексными коэффициентами степени
n,
учитывая кратные корни кратное количество
раз, равно n.
При этом все чисто комплексные корни
(если они есть) многочлена с вещественными
коэффициентами можно разбить на пары
сопряжённых одинаковой кратности, таким
образом, многочлен четной степени с
вещественными коэффициентами может
иметь только чётное число вещественных
корней, а нечётной — только нечётное.Корни
многочлена связаны с его коэффициентами
формулами Виета.
— (в общем случае комплексные) корни
многочлена
,
возможно с повторениями, при этом если
среди корней
многочлена
встречаются равные, то общее их значение
называется кратным корнем.Число
комплексных корней многочлена с
комплексными коэффициентами степени
n,
учитывая кратные корни кратное количество
раз, равно n.
При этом все чисто комплексные корни
(если они есть) многочлена с вещественными
коэффициентами можно разбить на пары
сопряжённых одинаковой кратности, таким
образом, многочлен четной степени с
вещественными коэффициентами может
иметь только чётное число вещественных
корней, а нечётной — только нечётное.Корни
многочлена связаны с его коэффициентами
формулами Виета.
25. Деление многочленов на двух член! Схема Хорнера?
Линейный двучлен есть многочлен первой степени: a x + b. Если разделить многочлен, содержащий букву x , на линейный двучлен x – b, где b – некоторое число (положительное или отрицательное), то остаток будет только многочленом нулевой степени, т.е. некоторым числом N , которое можно определить, не находя частного. Более точно, это число равно значению многочлена, получаемому при x = b. Это свойство вытекает из теоремы Безу: многочлен a0 xm + a1 xm-1 + a2 xm-2 + …+ am делится на двучлен x – b с остатком N = a0 bm + a1 bm-1 + a2 bm-2 + …+ am .
Д о к а з а т е л ь с т в о . В соответствии с определением операции деления многочленов имеем:
a0 xm + a1 xm-1 + a2 xm-2 + …+ am = ( x – b ) Q + N ,
где Q – некоторый многочлен, N – некоторое число.
Подставим x = b , тогда слагаемое ( x – b ) Q обращается в нуль, и мы получаем:
a0 bm + a1 bm-1 + a2 bm-2 + …+ am = N .
З а м е ч а н и е . При N = 0 число b является корнем уравнения:
a0 xm + a1 xm-1 + a2 xm-2 + …+ am = 0 .
Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена, а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида .
Схема Горнера
Если
![]() то при делении f(x)
на g(x)
частное q(x)
имеет вид
то при делении f(x)
на g(x)
частное q(x)
имеет вид
![]() где
где
![]() Остаток r находится по формуле
Остаток r находится по формуле
![]()

26 Неприводимый многочлен и их свойства
Неприводимый многочлен — многочлен, неразложимый на нетривиальные (неконстантные) многочлены. Неприводимые многочлены являются неприводимыми элементами кольца многочленов.
Определение
Неприводимый
многочлен над полем
―
многочлен
![]() от
переменных
над полем
является
простым элементом кольца
от
переменных
над полем
является
простым элементом кольца
![]() ,
то есть, непредставим в виде произведения
,
то есть, непредставим в виде произведения
![]() ,
где
,
где
![]() и
―
многочлены с коэффициентами из
,
отличные от констант.
и
―
многочлены с коэффициентами из
,
отличные от констант.
Многочлен называется абсолютно неприводимым, если он неприводим над алгебраическим замыканием поля коэффициентов. Абсолютно неприводимые многочлены одной переменной ― это многочлены 1-й степени и только они. В случае нескольких переменных существуют абсолютно неприводимые многочлены сколь угодно высокой степени — например, любой многочлен вида
![]()
абсолютно неприводим.
Свойства
Кольцо многочленов факториально: любой многочлен разлагается в произведение неприводимых многочленов, причем это разложение определено однозначно с точностью до постоянных множителей.
Над полем вещественных чисел любой неприводимый многочлен одной переменной имеет степень 1 или 2, причем многочлен 2-й степени неприводим тогда и только тогда, когда он имеет отрицательный дискриминант.
Над любым полем алгебраических чисел существуют неприводимый многочлен сколь угодно высокой степени; например, многочлен
 ,
где
,
где
 и
и
 ―
некоторое простое число, неприводим в
силу критерия
Эйзенштейна.
―
некоторое простое число, неприводим в
силу критерия
Эйзенштейна.Если
 —
конечное
поле
из
элементов,
а
—
натуральное число, то существует хотя
бы один неприводимый многочлен степени
n из
—
конечное
поле
из
элементов,
а
—
натуральное число, то существует хотя
бы один неприводимый многочлен степени
n из
 .
.Предположим ― целозамкнутое кольцо с полем частных (например
 и
и
 )
и
)
и
 ―
многочлен одной переменной со старшим
коэффициентом 1, тогда
в
,
причем
и
имеют
старший коэффициент 1, то
―
многочлен одной переменной со старшим
коэффициентом 1, тогда
в
,
причем
и
имеют
старший коэффициент 1, то
 .
.Редукционный критерий неприводимости. Пусть задан гомоморфизм областей целостности
 .
Если степень многочлена
.
Если степень многочлена
 совпадает
со степенью многочлена
и
неприводим
над полем частных области
,
то не существует разложения
,
где
совпадает
со степенью многочлена
и
неприводим
над полем частных области
,
то не существует разложения
,
где
 и
отличны от константы.
и
отличны от константы.Например, многочлен со старшим коэффициентом
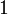 прост
в
прост
в
 (и,
следовательно, неприводим в
(и,
следовательно, неприводим в
 ),
если прост многочлен
,
полученный из
редукцией
коэффициентов по модулю простого
числа.
),
если прост многочлен
,
полученный из
редукцией
коэффициентов по модулю простого
числа.
27 Основная теорема поля комплексных чисел без доказательства и ее следствия
Определение. Полем называется непустое множество, для элементов которого определено два действия, называемых сложением и умножением, которые удовлетворяют следующим аксиомам:
1.
![]() (коммутативность
сложения);
(коммутативность
сложения);
2.
![]() (ассоциативность
сложения);
(ассоциативность
сложения);
3.
![]() (существование
нуля);
(существование
нуля);
4.
![]() (существование
противоположного элемента);
(существование
противоположного элемента);
5.
![]() (коммутативность
умножения);
(коммутативность
умножения);
6.
![]() (ассоциативность
умножения);
(ассоциативность
умножения);
7.
![]() (существование
единицы);
(существование
единицы);
8.
![]() (существование
обратного элемента);
(существование
обратного элемента);
9.
![]() (дистрибутивность);
(дистрибутивность);
10.
![]() (в
поле должно существовать хотя бы два
элемента).
(в
поле должно существовать хотя бы два
элемента).
Пример.
Поля:
![]() –
поле вещественных чисел,
–
поле вещественных чисел,
![]() –
поле рациональных чисел,
–
поле рациональных чисел,
![]()
Некоторые следствия из аксиом поля
1. Нуль есть только один.
Действительно,
пусть есть два нуля
![]() и
и
![]() :
:
![]()
Тогда
![]() и
и
![]() .
.
2. У числа есть только одно противоположное.
Действительно,
пусть их два
![]() и
и
![]() .
Тогда
.
Тогда
![]()
3.
![]() .
.
Действительно,
![]() .
.
4.
![]() .
.
Действительно,
![]() .
Аналогично
.
Аналогично
![]() .
Значит,
.
Значит,
![]() .
Кроме того,
.
Кроме того,
![]() .
Тогда
.
Тогда
![]()
и
![]() .
.
Определение поля комплексных чисел
Определение.
Полем комплексных чисел называется
множество
![]() ,
обладающее следующими свойствами:
,
обладающее следующими свойствами:
1. — поле;
2.
![]() (
содержит
).
При этом предполагается, что действия
в
в
применении к элементам из
приводят
к тем же результатам, что и действия в
.
(
содержит
).
При этом предполагается, что действия
в
в
применении к элементам из
приводят
к тем же результатам, что и действия в
.
3. Любое квадратное уравнение с вещественными коэффициентами имеет в поле корень.
4. Каждый элемент поля является корнем какого-либо квадратного уравнения с вещественными коэффициентами.
Рассмотрим уравнение
![]()
Оно
не имеет вещественных корней, но, по
аксиоме 3, имеет корень в поле
.
Один из корней этого уравнения зафиксируем
и обозначим
![]() (image)
— мнимая единица.
(image)
— мнимая единица.
Пусть
![]()

Теорема.
Любой элемент поля
можно
единственным образом представить в
виде
![]() ,
где
,
где
![]() .
.
28 Неприводимые многочлены над полем действительных чисел?
Неприводимый многочлен — многочлен, неразложимый на нетривиальные (неконстантные) многочлены. Неприводимые многочлены являются неприводимыми элементами кольца многочленов.
Определение
Неприводимый многочлен над полем ― многочлен от переменных над полем является простым элементом кольца , то есть, непредставим в виде произведения , где и ― многочлены с коэффициентами из , отличные от констант.
Многочлен называется абсолютно неприводимым, если он неприводим над алгебраическим замыканием поля коэффициентов. Абсолютно неприводимые многочлены одной переменной ― это многочлены 1-й степени и только они. В случае нескольких переменных существуют абсолютно неприводимые многочлены сколь угодно высокой степени — например, любой многочлен вида
абсолютно неприводим.
Свойства
Над полем вещественных чисел любой неприводимый многочлен одной переменной имеет степень 1 или 2, причем многочлен 2-й степени неприводим тогда и только тогда, когда он имеет отрицательный дискриминант.
Над любым полем алгебраических чисел существуют неприводимый многочлен сколь угодно высокой степени; например, многочлен , где и ― некоторое простое число, неприводим в силу критерия Эйзенштейна.
Если — конечное поле из элементов, а — натуральное число, то существует хотя бы один неприводимый многочлен степени n из .
Примеры
Следующие пять многочленов демонстрируют некоторые элементарные свойства неприводимых многочленов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Над
кольцом
![]() целых
чисел,
первые два многочлена — приводимые,
последние два — неприводимые. (Третий
вообще не является многочленом над
целыми числами).
целых
чисел,
первые два многочлена — приводимые,
последние два — неприводимые. (Третий
вообще не является многочленом над
целыми числами).
Над
полем
![]() рациональных
чисел,
первые три многочлена являются
приводимыми, двое других — неприводимыми.
рациональных
чисел,
первые три многочлена являются
приводимыми, двое других — неприводимыми.
Над
полем
действительных
чисел,
первые четыре многочлена — приводимые,
но
![]() является
неприводимым. В поле действительных
чисел неприводимыми являются линейные
многочлены и квадратичные многочлены
без действительных корней. Например
разложение многочлена
является
неприводимым. В поле действительных
чисел неприводимыми являются линейные
многочлены и квадратичные многочлены
без действительных корней. Например
разложение многочлена
![]() в
поле действительных чисел имеет вид
в
поле действительных чисел имеет вид
![]() .
Оба множителя в данном разложении
являются неприводимыми многочленами.
.
Оба множителя в данном разложении
являются неприводимыми многочленами.
Над
полем
комплексных
чисел,
все пять многочленов — приводимые.
Фактически, каждый отличный от константы
многочлен
![]() над
может
быть разложен на множители вида:
над
может
быть разложен на множители вида:
![]()
где
—
степень
многочлена,
![]() —
старший коэффициент,
—
старший коэффициент,
![]() —
корни
.
Поэтому единственными неприводимыми
многочленами над
являются
линейные многочлены (основная
теорема алгебры).
—
корни
.
Поэтому единственными неприводимыми
многочленами над
являются
линейные многочлены (основная
теорема алгебры).
Конечные поля
Многочлены
с целочисленными коэффициентами, которые
являются неприводимыми над полем
могут
быть приводимыми над конечным
полем.
Например, многочлен
![]() является
неприводимым над
,
но над полем
является
неприводимым над
,
но над полем
![]() из
двух элементов мы имеем:
из
двух элементов мы имеем:
![]()
29 Неприводимые многочлены над полем рациональных чисел. Критерий Эйзенштейна?
Неприводимый многочлен над полем ― многочлен от переменных над полем является простым элементом кольца , то есть, непредставим в виде произведения , где и ― многочлены с коэффициентами из , отличные от констант.Многочлен называется абсолютно неприводимым, если он неприводим над алгебраическим замыканием поля коэффициентов. Абсолютно неприводимые многочлены одной переменной ― это многочлены 1-й степени и только они. В случае нескольких переменных существуют абсолютно неприводимые многочлены сколь угодно высокой степени — например, любой многочлен вида
абсолютно неприводим.
Крите́рий
Э́йзенштейна
— признак неприводимости
многочлена.
Несмотря на (традиционное) название,
является именно признаком, то есть
достаточным условием — но вовсе не
необходимым, Формулировка
Пусть
![]() -
многочлен
над факториальным
кольцом
R
(
-
многочлен
над факториальным
кольцом
R
(![]() ),
и для некоторого неприводимого элемента
выполняются
следующие условия:
),
и для некоторого неприводимого элемента
выполняются
следующие условия:
 ,
, для
любого i от 0 до n-1,
для
любого i от 0 до n-1, .
.
Тогда
многочлен
![]() неприводим
над F
— полем
частных
кольца R.Наиболее
часто этот критерий применяется, когда
R
— кольцо целых чисел
,
а F
— поле рациональных чисел
.Доказательство
Предположим обратное:
неприводим
над F
— полем
частных
кольца R.Наиболее
часто этот критерий применяется, когда
R
— кольцо целых чисел
,
а F
— поле рациональных чисел
.Доказательство
Предположим обратное:
![]() ,
где
,
где
![]() и
и
![]() многочлены
над F
ненулевых степеней. Из леммы
Гаусса
следует, что их можно рассматривать как
многочлены над R.
Имеем:
многочлены
над F
ненулевых степеней. Из леммы
Гаусса
следует, что их можно рассматривать как
многочлены над R.
Имеем:
![]()
По
условию
![]() и
R
факториально, поэтому либо
и
R
факториально, поэтому либо
![]() либо
либо
![]() ,
но не то и другое вместе ввиду того, что
.
Пусть
и
,
но не то и другое вместе ввиду того, что
.
Пусть
и
![]() .
Все коэффициенты
.
Все коэффициенты
![]() не
могут делиться на
,
так как иначе бы это было бы верно для
.
Пусть
—
минимальный индекс, для которого
не
могут делиться на
,
так как иначе бы это было бы верно для
.
Пусть
—
минимальный индекс, для которого
![]() не
делится на
.
Отсюда следует:
не
делится на
.
Отсюда следует:
![]()
Так
как
![]() и
и
![]() для
всех
для
всех
![]() то
то
![]() ,
но это невозможно, так как по условию
и
,
но это невозможно, так как по условию
и
![]() .
Теорема доказана.
.
Теорема доказана.
30 Векторная пространства. Линейная оболочка векторов?
Линейное,
или векторное
пространство
![]() над
полем
над
полем
![]() —
это непустое
множество
—
это непустое
множество
![]() ,
на котором введены операции
,
на котором введены операции
сложения, то есть каждой паре элементов множества
 ставится
в соответствие элемент того же множества,
обозначаемый
ставится
в соответствие элемент того же множества,
обозначаемый
 и
иумножения на скаляр (то есть элемент поля ), то есть любому элементу
 и
любому элементу
и
любому элементу
 ставится
в соответствие единственный элемент
из
,
обозначаемый
ставится
в соответствие единственный элемент
из
,
обозначаемый
 .
.
При этом на операции накладываются следующие условия:
 ,
для любых
(коммутативность
сложения);
,
для любых
(коммутативность
сложения); ,
для любых
,
для любых
 (ассоциативность
сложения);
(ассоциативность
сложения);существует такой элемент
 ,
что
,
что
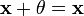 для
любого
(существование
нейтрального элемента относительно
сложения),
в частности
не
пусто;
для
любого
(существование
нейтрального элемента относительно
сложения),
в частности
не
пусто;для любого существует такой элемент
 ,
что
,
что
 (существование
противоположного элемента относительно
сложения).
(существование
противоположного элемента относительно
сложения). (ассоциативность
умножения на скаляр);
(ассоциативность
умножения на скаляр); (унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор). (дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на вектор относительно
сложения скаляров); (дистрибутивность
умножения на скаляр относительно
сложения векторов).
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Элементы множества называют векторами, а элементы поля — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы
Линейная
оболочка
![]() подмножества
линейного
пространства
—
пересечение всех подпространств
,
содержащих
.
Линейная оболочка является подпространством
.
Линейная оболочка также называется
подпространством,
порожденным
.
Говорят также, что линейная оболочка
натянута
на
множество
.
Линейная оболочка
состоит
из всевозможных линейных комбинаций
различных конечных подсистем элементов
из
.
В частности, если
—
конечное множество, то
состоит
из всех линейных комбинаций элементов
.
Если
—
линейно независимое множество, то оно
является базисом
и
тем самым определяет его размерность.
подмножества
линейного
пространства
—
пересечение всех подпространств
,
содержащих
.
Линейная оболочка является подпространством
.
Линейная оболочка также называется
подпространством,
порожденным
.
Говорят также, что линейная оболочка
натянута
на
множество
.
Линейная оболочка
состоит
из всевозможных линейных комбинаций
различных конечных подсистем элементов
из
.
В частности, если
—
конечное множество, то
состоит
из всех линейных комбинаций элементов
.
Если
—
линейно независимое множество, то оно
является базисом
и
тем самым определяет его размерность.
31. Базис и ранг системы векторов?
Определение
1.
Рангом системы векторов называется
максимальное число линейно независимых
векторов системы.
Определение
2.
Базисом системы векторов называется
максимальная линейно независимая
подсистема данной системы векторов.
Теорема.
Если система векторов
![]() линейно-зависима,
то она эквивалентна системе
линейно-зависима,
то она эквивалентна системе
![]()
Доказательстово.
Действительно, пусть
![]() одновременно
неравные нулю числа такие, что
одновременно
неравные нулю числа такие, что
![]() .
Предположим, что
.
Предположим, что
![]() S
S
![]() 0
, разделим эту сумму на
S,
получим:
0
, разделим эту сумму на
S,
получим:
![]() или
или
![]() ,
где
,
где
![]() .
.
Заменим
систему векторов
![]() эквивалентной
системой
эквивалентной
системой
![]() с
помощью следующего элементарного
преобразования:
с
помощью следующего элементарного
преобразования:
![]() при
при
![]() и
и
![]() .
Тогда вектор
.
Тогда вектор
![]() .
Поменяв местами векторы
.
Поменяв местами векторы
![]() и
и
![]() получим
систему вида
.
Что и требовалось доказать.
получим
систему вида
.
Что и требовалось доказать.
Следствие.
Произвольную систему векторов
элементарными
преобразованиями можно привести к
системе вида
![]() ,
где
,
где
![]() линейно
независимая система векторов.
линейно
независимая система векторов.
Число
![]() будем
называть рангом системы векторов
,
а систему
будем
называть рангом системы векторов
,
а систему
– базисом системы векторов .
Отметим, что ранг системы векторов не зависит от конкретной цепочки элементарных преобразований. Максимально независимая подсистема системы векторов называется ее базисом; векторы, входящие в базис, называются базисными векторами. Будем называть рангом системы векторов число векторов ее базиса. Понятно, что если ранг системы векторов меньше числа k ее векторов, то она может иметь несколько базисов. Понятие базиса распространяется и на пространство Rn, которое является системой, содержащей всю бесконечную совокупность n-мерных векторов. Определение 3. Система n векторов называется базисом пространства Rn,если: 1) векторы этой системы линейно независимы; 2) всякий вектор из Rn линейно выражается через векторы данной системы.
32. Линейная зависимость и линейная независимость систем векторов
Рассмотрим
набор из p
n-мерных
векторов,
обозначим их следующим образом
![]() .
Составим линейную комбинацию этих
векторов и произвольных чисел
.
Составим линейную комбинацию этих
векторов и произвольных чисел
![]() (действительных
или комплексных):
(действительных
или комплексных):
![]() .
Отталкиваясь от определения операций
над n-мерными
векторами, а так же свойств операций
сложения векторов и умножения вектора
на число, можно утверждать, что записанная
линейная комбинация представляет собой
некоторый n-мерный
вектор
.
Отталкиваясь от определения операций
над n-мерными
векторами, а так же свойств операций
сложения векторов и умножения вектора
на число, можно утверждать, что записанная
линейная комбинация представляет собой
некоторый n-мерный
вектор
![]() ,
то есть,
,
то есть,
![]() .Так
мы подошли к определению линейной
зависимости системы векторов
.Определение.Если
линейная комбинация
может
представлять собой нулевой вектор
тогда, когда среди чисел
есть
хотя бы одно, отличное от нуля, то система
векторов
называется
линейно
зависимой.
Определение.
Если линейная комбинация
представляет
собой нулевой вектор только тогда, когда
все числа
равны
нулю, то система векторов
называется
линейно
независимой.
Свойства
линейной зависимости и независимости.
На основании данных определений,
сформулируем и докажем свойства
линейной зависимости и линейной
независимости системы векторов.
1.Если к линейно зависимой системе
векторов
добавить
несколько векторов, то полученная
система будет линейно зависимой.
Доказательство.Так
как система векторов
линейно
зависима, то равенство
.Так
мы подошли к определению линейной
зависимости системы векторов
.Определение.Если
линейная комбинация
может
представлять собой нулевой вектор
тогда, когда среди чисел
есть
хотя бы одно, отличное от нуля, то система
векторов
называется
линейно
зависимой.
Определение.
Если линейная комбинация
представляет
собой нулевой вектор только тогда, когда
все числа
равны
нулю, то система векторов
называется
линейно
независимой.
Свойства
линейной зависимости и независимости.
На основании данных определений,
сформулируем и докажем свойства
линейной зависимости и линейной
независимости системы векторов.
1.Если к линейно зависимой системе
векторов
добавить
несколько векторов, то полученная
система будет линейно зависимой.
Доказательство.Так
как система векторов
линейно
зависима, то равенство
![]() возможно
при наличии хотя бы одного ненулевого
числа из чисел
.
Пусть
возможно
при наличии хотя бы одного ненулевого
числа из чисел
.
Пусть
![]() .
Добавим к исходной системе векторов
еще s
векторов
.
Добавим к исходной системе векторов
еще s
векторов
![]() ,
при этом получим систему
,
при этом получим систему
![]() .
Так как
и
.
Так как
и
![]() ,
то линейная комбинация векторов этой
системы вида
,
то линейная комбинация векторов этой
системы вида
 представляет
собой нулевой вектор, а
.
Следовательно, полученная система
векторов является линейно зависимой.
1.Если из линейно независимой системы
векторов
исключить
несколько векторов, то полученная
система будет линейно независимой.
Доказательство.
Предположим, что полученная система
линейно зависима. Добавив к этой системе
векторов все отброшенные векторы, мы
получим исходную систему векторов. По
условию – она линейно независима, а в
силу предыдущего свойства линейной
зависимости она должна быть линейно
зависимой. Мы пришли к противоречию,
следовательно, наше предположение
неверно. 1.Если в системе векторов
есть
хотя бы один нулевой вектор, то такая
система линейно зависимая.
Доказательство.Пусть
вектор
представляет
собой нулевой вектор, а
.
Следовательно, полученная система
векторов является линейно зависимой.
1.Если из линейно независимой системы
векторов
исключить
несколько векторов, то полученная
система будет линейно независимой.
Доказательство.
Предположим, что полученная система
линейно зависима. Добавив к этой системе
векторов все отброшенные векторы, мы
получим исходную систему векторов. По
условию – она линейно независима, а в
силу предыдущего свойства линейной
зависимости она должна быть линейно
зависимой. Мы пришли к противоречию,
следовательно, наше предположение
неверно. 1.Если в системе векторов
есть
хотя бы один нулевой вектор, то такая
система линейно зависимая.
Доказательство.Пусть
вектор
![]() в
этой системе векторов является нулевым.
Предположим, что исходная система
векторов линейно независима. Тогда
векторное равенство
возможно
только тогда, когда
в
этой системе векторов является нулевым.
Предположим, что исходная система
векторов линейно независима. Тогда
векторное равенство
возможно
только тогда, когда
![]() .
Однако, если взять любое
.
Однако, если взять любое
![]() ,
отличное от нуля, то равенство
все
равно будет справедливо, так как
,
отличное от нуля, то равенство
все
равно будет справедливо, так как
![]() .
Следовательно, наше предположение
неверно, и исходная система векторов
линейно зависима. 1Если система векторов
линейно
зависима, то хотя бы один из ее векторов
линейно выражается через остальные.
Если система векторов
линейно
независима, то ни один из векторов не
выражается через остальные.
.
Следовательно, наше предположение
неверно, и исходная система векторов
линейно зависима. 1Если система векторов
линейно
зависима, то хотя бы один из ее векторов
линейно выражается через остальные.
Если система векторов
линейно
независима, то ни один из векторов не
выражается через остальные.
33. Признаки линейной зависимости векторов
Теорема.
При
умножении вектора на число каждая из
его координат умножается на это число,
а при сложении складываются соответствующие
координаты.Доказательство.
Пусть даны два произвольных вектора xи
yи
некоторое произвольное число
![]() .
Разложим векторы по базису l1,
l2,
..., ln,
получим x=x1l1+x2l2+...+xnlnи
y=y1l1+y2l2+...+ynlnи
найдем произведение
.
Разложим векторы по базису l1,
l2,
..., ln,
получим x=x1l1+x2l2+...+xnlnи
y=y1l1+y2l2+...+ynlnи
найдем произведение
![]()
![]()
и сумму x + y
x+y = (x1l1+x2l2+...+xnln)+(y1l1+y2l2+...+ynln)=
=(x1+y1)l1+(x2+y2)l2+...+(xn+yn)ln =>
=> x+y = [(x1+y1);(x2+y2);...;(xn+yn)].
Доказанная теорема очень важна в математике, так как из нее следует признак линейной зависимости и независимости векторов. Покажем это. Пусть в некотором n -мерном пространстве Rзадана система векторов:
|
(1) |
Умножим
каждый из векторов на некоторое число
![]() и
сложим их все друг с другом. В результате
получим линейную комбинацию этих же
векторов, которая является новым
вектором, равным, по определению нулю
и
сложим их все друг с другом. В результате
получим линейную комбинацию этих же
векторов, которая является новым
вектором, равным, по определению нулю
|
(2) |
Распишем систему (2) в координатной форме
|
(3) |
откуда следует однородная система уравнений
|
(4) |
из коэффициентов которой составляют матрицу
|
(5) |
Равенство (3) эквивалентно равенствам (2) и (4). На основании теоремы можно утверждать, что векторы системы (1) линейно независимы тогда и только тогда, когда однородная система (4) имеет единственное нулевое решение, что на практике обозначает, что ранг матрицы (5) равен количеству векторов системы m
34 Необходимые и достаточные условия линейной независимости систем векторов?
. Система элементов линейного пространства {a1,…,an} называется линейно
независимой,
если
ее линейная комбинация равна нулю только
с нулевыми коэффициентами:

Имеют место несколько простых утверждений.
Теорема
1 (необходимое
и достаточное условие линейной
независимости).
a1,…,an
– линейно зависима
![]() когда
хотя бы один из элементов является
линейной комбинацией остальных.
когда
хотя бы один из элементов является
линейной комбинацией остальных.
{1.(необходимость:
{ak}
– л.з. ):
 .
Пусть, для определенности,
.
Пусть, для определенности,
![]() а1
– линейная комбинация остальных.
а1
– линейная комбинация остальных.
2.(достаточность:
am
– л.к.):
 }
}
Теорема
(необходимое и достаточное условие
линейной независимости в координатной
форме). Cистема
векторов
![]() из
Rn
линейно
независима тогда и только тогда, когда
отличен от нуля определитель, строками
(столбцами) которого являются компоненты
векторов системы:
из
Rn
линейно
независима тогда и только тогда, когда
отличен от нуля определитель, строками
(столбцами) которого являются компоненты
векторов системы:
Следствиями из этой теоремы являются следующие утверждения:
если
 ,
то система векторов
из
Rn
— линейно зависима;
,
то система векторов
из
Rn
— линейно зависима;любая система векторов
 из
Rn,
k
> n —
линейно зависима
из
Rn,
k
> n —
линейно зависима
Теорема 2. Если один из элементов системы равен нулю, то вся система линейно зависима.
{![]() }
}
Теорема 3. Если подсистема линейно зависима, то и вся система линейно зависима.
{![]() }
}
35 Линейная зависимость двух векторов на прямой
Определение:
Система векторов
![]()
называется линейно зависимой, если хотя бы одна нетривиальная
линейная комбинация векторов системы обращается в нуль, т.е. имеет место
равенство
![]() ,
при
,
при
![]()
.
Система векторов не являющаяся линейно зависимой называется линейно независимой.
Определение: Система векторов
называется линейно независимой, если равенство нулю линейной
комбинации векторов системы возможно лишь в случае ее тривиальности, т.е. из
того,
что
следует
![]()
.
Теорема: Если хотя бы один из векторов системы является нулевым, то эта
система является линейно зависимой.
Действительно,
из векторов системы
![]()
можно
составить линейную комбинацию
![]()
, которая не является тривиальной.
Теорема: Если часть системы векторов линейно зависима то и вся система
векторов линейно зависима.



Действительно,
если система векторов
![]()
линейно
зависима, то существует нетривиальная
линейная комбинация
![]()
.
Для любой системы векторов
![]()
линейная
комбинация
![]() также
также
является нетривиальной.
Теорема: Необходимым и достаточным условием линейной зависимости двух
векторов является их коллинеарность.
Действительно, либо оба коллинеарных вектора равны нулю, и тогда равна нулю
любая их линейная комбинация (в том числе и нетривиальная), либо один из них не
нуль, и тогда, в силу теоремы из второго раздела, другой отличается от него на
числовой
множитель. Запишем это:
![]()
.
Но эта же запись означает, что
![]()
, и мы имеем нетривиальную линейную комбинацию, равную нулю.
Наоборот,
допустим, что два неколлинеарных вектора
![]()
и
![]() линейно
зависимы. Тогда
линейно
зависимы. Тогда
существуют
коэффициенты λ и μ такие, что
![]()
,
причем, например, λ ≠ 0. Это означает,
что

, и векторы коллинеарны, вопреки нашему предположению.
Следствие: Если два вектора неколлинеарны, то они линейно независимы.
Теорема:
Любой вектор
![]()
лежащий в одной плоскости с неколлинеарными векторами
и , может быть представлен в
виде линейной комбинации этих векторов (т.е. найдутся такие вещественные числа
λ
и μ, что
![]() ).
Такое
).
Такое
представление единственно.
Заметим, прежде всего, что оба вектора
и отличны от нуля, так как если
бы хоть один из них был нулевым, то они были бы коллинеарны. Если вектор
коллинеарен одному из данных векторов, то утверждение сводится к теореме из
второго раздела.
В общем случае перенесем все три вектора в одну точку О (рис. 6). Через
конец
C
вектора
![]()
проведем прямые CР и CQ, параллельные векторам
и
.
Тогда
![]()
,
причем векторы
![]() и
и
![]()
коллинеарны соответственно и
. В силу теоремы из второго раздела существуют и определены однозначно такие
числа
λ и μ, что
![]() ,
,
![]()
.
Таким образом,
![]() ,
что и
,
что и
требовалось.
Допустим
теперь, что существует другая линейная
комбинация
![]()
, равная , причем, например
λ
≠ σ. Тогда
![]() ,
,
так как иначе мы имели бы две прямые, проходящие через точку C
параллельно вектору . Из
последнего равенства вытекает, что σ = λ, в противоречие с нашим
предположением.
36 Линейная зависимость трех векторов на плоскости
Утверждение 1. На прямой (на плоскости и в пространстве) существует нулевой вектор (соответственно два неколлиниарных и три некомпланарных вектора) . |
Доказательство.
В случае прямой достаточно взять две
несовпадающие точки О и А(рис. 1, а),
тогда вектор а =
|
Утверждение 2. На прямой ( на плоскости и в пространстве) всякий вектор линейно выражается через любой ненулевой вектор (соответственно любые два неколлиниарных и любые три некомпанарных вектора). |
Доказательство. 1. Пусть a, b− векторы на прямой и a ≠ 0. Отложим их от одной точки О прямой. Пусть а = , b = (рис. 2, а). Если b = 0, то b = 0a. Если b ≠ 0, то, взяв
согласно
определению произведения вектора на
число получим, что b = αa.
2. Пусть а,
b, с − векторы плоскости и a, b неколлиниарны
(значит, ни один из них не равен 0).
Отложим эти векторы от одной точки О
плоскости. Пусть а =
,
b =
,
с =
(рис.
2, б). Если с = 0, то с = 0а + 0b. Если с ≠ 0,
то проведем из точки С прямые,
параллельные прямым ОВ и ОА, до
пересечения с прямыми ОА и ОВ
соответственно. Пусть точки А1,
B1
− точки пересечения этих прямых
(существование точек пересечения
следует из неколлиниарности
и
).
Тогда
=
1
+
1.
Отсюда и из первой части утверждения
получим, что c = αa + βb.
3. Пусть a, b,
c, d − векторы пространства и a, b, c
некомпланарны (значит, попарно
неколлиниарны и, тем более, ни один
из них не равен 0). Отложим эти векторы
от одной точки О. Пусть а =
,
b =
,
с =
,
d =
|
Теорема 2.7. Два вектора линейно зависимы тогда и только тогда, когда они коллиниарны. |
Теорема 2.8. Три вектора линейно зависимы тогда и только тогда, когда они компланарны. |
Доказательство. Необходимость. Пусть векторы a, b, c линейно зависимы, тогда один из них линейно выражается через другие. Пусть c = αa + βb. Усли а и b коллиниарны, то а, b, с коллиниарны и, тем более, компланарны. Если a и b неколлинеарны, то отложим векторы a, b, c от одной точки (рис. 2, б). Тогда вектор с, являясь диагональю параллелограмма, построенного на векторах αa и βb, окажется в той же плоскости, что и a, b. Значит, a, b, c компланарны. Достаточность.Пусть a, b, c компланарны, т.е. параллельны одной плоскости. Будем считать, что a, b неколлиниарны (так как если a, b коллиниарны, то линейная зависимость a, b, c следует из линейной зависимости подсистемы). Отложим a, b и с от одной точки. Тогда они окажутся в одной плоскости и на основании утверждения 2 будем иметь c = αa + βb. В силу теоремы 2.2 отсюда следует, что векторы a, b, c линейно зависимы. Теорема доказана. |
37 Линейная зависимость четырех векторов в пространстве
Теорема 2.9. Любые четыре вектора линейно зависимы. |
Доказательство. Будем считать, что в четверке векторов a, b, c, d векторы a, b, c некомпланарны (так как если a, b, c компланарны, то линейная зависимость a, b, c, d вытекает из линейной зависимости подсистемы). Тогда на основании утверждения 2 будем иметь d = αa + βb + γc. В силу теоремы 2.2 отсюда следует, что векторы a, b, c, d линейно зависимы. Теорема доказана. |
Если первые три вектора -- некомпланарные, то четвертый является их линейной комбинацией
Предложение
Система
векторов
![]() линейно
зависима тогда и только тогда, когда
один из векторов системы является
линейной комбинацией остальных векторов
этой системы.
линейно
зависима тогда и только тогда, когда
один из векторов системы является
линейной комбинацией остальных векторов
этой системы.
Доказательство.
Пусть система векторов линейно зависима.
Тогда существует такой набор коэффициентов
![]() ,
что
,
что
![]() ,
причем хотя бы один коэффициент отличен
от нуля. Предположим, что
,
причем хотя бы один коэффициент отличен
от нуля. Предположим, что
![]() .
Тогда
.
Тогда

то
есть
![]() является
линейной комбинацией остальных векторов
системы.
является
линейной комбинацией остальных векторов
системы.
Пусть
один из векторов системы является
линейной комбинацией остальных векторов.
Предположим, что это вектор
,
то есть
![]() .
Очевидно, что
.
Очевидно, что
![]() .
Получили, что линейная комбинация
векторов системы равна нулю, причем
один из коэффициентов отличен от нуля
(равен
.
Получили, что линейная комбинация
векторов системы равна нулю, причем
один из коэффициентов отличен от нуля
(равен
![]() ).
).
38 . Базис и размерность над пространством
Определение. Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.
Определение.Базис
векторного пространства
– это упорядоченная совокупность
линейно независимых векторов этого
пространства, число которых равно
размерности пространства. Приведем
некоторые рассуждения, основываясь на
этих определениях. Рассмотрим пространство
n-мерных
векторов. Покажем, что размерность этого
пространства равна n.
Возьмем систему из n
единичных векторов вида
 Примем
эти векторы в качестве строк матрицы
А.
В этом случае матрица А
будет единичной матрицей размерности
n
на n.
Ранг этой матрицы равен n
(при необходимости смотрите статью ранг
матрицы: определение, методы нахождения).
Следовательно, система векторов
Примем
эти векторы в качестве строк матрицы
А.
В этом случае матрица А
будет единичной матрицей размерности
n
на n.
Ранг этой матрицы равен n
(при необходимости смотрите статью ранг
матрицы: определение, методы нахождения).
Следовательно, система векторов
![]() линейно
независима, причем к этой системе нельзя
добавить ни одного вектора, не нарушив
ее линейной независимости. Так как число
векторов в системе
равно
n,
то размерность
пространства n-мерных
векторов равна n,
а единичные векторы
являются
базисом этого пространства.
Из последнего утверждения и определения
базиса можно сделать вывод, что любая
система n-мерных
векторов, число векторов в которой
меньше n,
не является базисом.Теперь
переставим местами первый и второй
вектор системы
.
Легко показать, что полученная система
векторов
линейно
независима, причем к этой системе нельзя
добавить ни одного вектора, не нарушив
ее линейной независимости. Так как число
векторов в системе
равно
n,
то размерность
пространства n-мерных
векторов равна n,
а единичные векторы
являются
базисом этого пространства.
Из последнего утверждения и определения
базиса можно сделать вывод, что любая
система n-мерных
векторов, число векторов в которой
меньше n,
не является базисом.Теперь
переставим местами первый и второй
вектор системы
.
Легко показать, что полученная система
векторов
![]() также
является базисом n-мерного
векторного пространства. Составим
матрицу, приняв ее строками векторы
этой системы. Эта матрица может быть
получена из единичной матрицы перестановкой
местами первой и второй строк,
следовательно, ее ранг будет равен n.
Таким образом, система из n
векторов
линейно
независима и является базисом n-мерного
векторного пространства.Если переставить
местами другие векторы системы
,
то получим еще один базис.Если взять
линейно независимую систему не единичных
векторов, то она также является базисом
n-мерного
векторного пространства.
также
является базисом n-мерного
векторного пространства. Составим
матрицу, приняв ее строками векторы
этой системы. Эта матрица может быть
получена из единичной матрицы перестановкой
местами первой и второй строк,
следовательно, ее ранг будет равен n.
Таким образом, система из n
векторов
линейно
независима и является базисом n-мерного
векторного пространства.Если переставить
местами другие векторы системы
,
то получим еще один базис.Если взять
линейно независимую систему не единичных
векторов, то она также является базисом
n-мерного
векторного пространства.
39 Координаты вектора в данном базисе . Координаты точки
1.
Пусть e1
− базис V1
и а − произвольный вектор из V1.
Отложив эти векторы от
одной точки
О прямой V1
(рис.
2,а)
, так что e1
=
![]() ,
а
=
1,
получим, что а
= xe1,
где
,
а
=
1,
получим, что а
= xe1,
где
 (3.1.1)
(3.1.1)
Введем на прямой V1 направление: пусть положительное направление на прямой совпадает с направлением базисного вектора e1. Тогда согласно (3.1.1) и (1.1.1) получим
 (3.1.2)
(3.1.2)
Ось, положительное направление которой совпадает с направлением вектора e1, будем называть осью, определенной вектором e. 2. Пусть e1, e2 − базис V2 и а − произвольный вектор из V2. Отложив эти векторы от одной точки О плоскости V2 (рис. 2,б), так что e1 = 1, e2 = 2, а = , введя направления на прямых ОЕ1 и OE2, совпадающие с направлениями базисных векторов e1 и e2, получим в соответствии с (3.1.2), что а = xe1 + ye2,
 (3.1.3)
(3.1.3)
где А1, A2 − проекции точки А на прямые OE1 и OE2 параллельно соответственно прямым OE2 и OE1. 3. Пусть e1, e2, e3 − базис V3 и a − произвольный вектор из V3. Поступая аналогично (рис. 2,в), получим а = xe1 + ye2 + ze3,
 (3.1.4)
(3.1.4)
где A1, A2, A3 − проекции точки А на прямые OE1, OE2 и OE3,параллельные соответственно плоскостям OE2E3, OE1E3 и OE1E2.
Координатами точки А в аффинной системе координат {O; e1, e2, e3} называются координаты радиус - вектора rA этой точки в базисе e1, e2, e3. Тот факт, что точка А имеет координаты x, y, z, обозначают символом А( x, y, z). Итак,
rA = xe1 + ye2 + ze3 ⇔ A(x, y, z). 3.2.1
Замечание 1.Из определения следует, что любая точка А пространства в заданной системе координат имеет координаты, причем точки A1(x1, y1, z1) и A2(x2, y2, z2) совпадают тогда и только тогда, когда x1 = x2, y1 = y2, z1 = z2.
40 Скалярное произведение векторов свойства
Скалярным
произведением двух векторов называется
число, равное произведению модулей этих
векторов на косинус угла между
ними.Скалярное произведение векторов
![]() ,
,
![]() обозначается
символом
обозначается
символом
![]() (порядок
записи сомножителей безразличен, то
есть
(порядок
записи сомножителей безразличен, то
есть
![]() ).Если
угол между векторами
,
обозначить
через
).Если
угол между векторами
,
обозначить
через
![]() ,
то их скалярное произведение можно
выразить формулой
,
то их скалярное произведение можно
выразить формулой
![]() (1)
(1)
Скалярное произведение векторов , можно выразить также формулой
![]() ,
или
,
или
 .
.
Из
формулы (1) следует, что
![]() ,
если
-
острый угол,
,
если
-
острый угол,
![]() ,
если
-
тупой угол;
,
если
-
тупой угол;
![]() в
том и только в том случае, когда векторы
и
перпендикулярны
(в частности,
,
если
в
том и только в том случае, когда векторы
и
перпендикулярны
(в частности,
,
если
![]() или
или
![]() ).
).
Скалярное
произведение
![]() называется
скалярным квадратом вектора и обозначается
символом
называется
скалярным квадратом вектора и обозначается
символом
![]() .
Из формулы (1) следует, что скалярный
квадрат вектора равен квадрату его
модуля:
.
Из формулы (1) следует, что скалярный
квадрат вектора равен квадрату его
модуля:
 .
.
Если векторы и заданы своими координатами:
![]() ,
,
![]() ,
,
то их скалярное произведение может быть вычислено по формуле
![]() .
.
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов
![]() .
.
Угол между векторами
, ,
дается
формулой
 ,
или в координатах
,
или в координатах
 .
.
Проекция
произвольного вектора
![]() на
какую-нибудь ось uопределяется формулой
на
какую-нибудь ось uопределяется формулой
![]() ,
,
где
![]() -
единичный вектор, направленный по оси
u. Если даны углы
-
единичный вектор, направленный по оси
u. Если даны углы
![]() ,
,
![]() ,
,
![]() ,
которые оси uсоставляет с координатными
осями, то
,
которые оси uсоставляет с координатными
осями, то
![]() и
для вычисления вектора
и
для вычисления вектора
![]() может
служить формула
может
служить формула
![]() .
.
2.Свойтсва скалярного произведения векторов.
1. Скалярное произведение обладает переместительным свойством: ab=ba


41.
Векторное
произведение векторов. Свойства.
Векторное
произведение —это псевдовектор, перпендикулярный плоскости,
построенной по двум сомножителям,
являющийся результатом бинарной
операции «векторное
умножение» над векторами в
трёхмерном Евклидовом
пространстве.
Произведение не является ни коммутативным,
ни ассоциативным (оно
является антикоммутативным)
и отличается от скалярного
произведения векторов.
Векторное произведение определено
только в трёхмерном и семимерном пространствах.
Результат векторного произведения, как
и скалярного, зависит от метрики Евклидова
пространства.В отличие от формулы для
вычисления по координатам векторов скалярного
произведения в
трёхмерной прямоугольной
системе координат,
формула для векторного произведения
зависит от ориентации прямоугольной
системы координат или, иначе, её
«хиральности».
Иными словами векторным
произведением можно назвать произведение
векторов ![]() и
и ![]() называется
вектор
называется
вектор ![]() ,
который определяется следующими
условиями:
1) Его модуль равен
,
который определяется следующими
условиями:
1) Его модуль равен ![]()
![]() где
где ![]() -
угол между векторами
и
.
2) Вектор
перпендикулярен
к плоскости, определяемой перемножаемыми
векторами
и
.
3) Вектор
направлен
так, что наблюдателю, смотрящему с его
конца на перемножаемые векторы
и
,
кажется, что для кратчайшего совмещения
первого сомножителя со вторым первый
сомножитель нужно вращать против часовой
стрелки (см. рисунок).
-
угол между векторами
и
.
2) Вектор
перпендикулярен
к плоскости, определяемой перемножаемыми
векторами
и
.
3) Вектор
направлен
так, что наблюдателю, смотрящему с его
конца на перемножаемые векторы
и
,
кажется, что для кратчайшего совмещения
первого сомножителя со вторым первый
сомножитель нужно вращать против часовой
стрелки (см. рисунок).
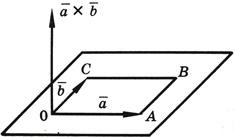
Основные
свойства векторного произведения:
1) Векторное
произведение ![]() равно
нулю, если векторы
и
коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
2) При перестановке
местами векторов сомножителей векторное
произведение меняет знак на противоположный
равно
нулю, если векторы
и
коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
2) При перестановке
местами векторов сомножителей векторное
произведение меняет знак на противоположный
![]()
![]()
![]()
С помощью векторного произведения можно 1)вычислить площадь параллелограмма и треугольника:

![]()

Пример.
Найти площадь параллелограмма,
построенного на векторах ![]() ,
, ![]() ,
если
,
если ![]() ,
,  .
.
Решение.  ,
,
Поэтому
 .
2)Векторное произведение позволяет
проверить коллинеарность двух векторов:
.
2)Векторное произведение позволяет
проверить коллинеарность двух векторов: ![]() 3)Векторное произведение позволяет
по двум заданным векторам указать
перпендикулярный им вектор
4) Механическая интерпретация векторного
произведения.
3)Векторное произведение позволяет
по двум заданным векторам указать
перпендикулярный им вектор
4) Механическая интерпретация векторного
произведения.
42.
Смешанное произведение векторов.
Нахождение объема параллелепипеда с
помощью смешанного произведения.
Смешанным
произведением трех векторов ![]() ,
, ![]() ,
, ![]() называется
число
называется
число ![]() .
Геометрический
смысл смешанного произведения: модуль
смешанного произведения трех векторов
численно равен объему параллелепипеда,
построенного на этих векторах.Пусть
ребрами параллелограмма являются
векторы
,
,
образующие
правую тройку векторов и вектор
.
Геометрический
смысл смешанного произведения: модуль
смешанного произведения трех векторов
численно равен объему параллелепипеда,
построенного на этих векторах.Пусть
ребрами параллелограмма являются
векторы
,
,
образующие
правую тройку векторов и вектор ![]() Имеем
Имеем ![]() ∙
∙![]() ,
так как
,
так как ![]() –
площадь основания построенного на
векторах
–
площадь основания построенного на
векторах ![]() ,
а
,
а ![]() –
высота параллелограмма, то
–
высота параллелограмма, то ![]() –
объем параллелограмма построенного на
правой тройке векторов
,
–
объем параллелограмма построенного на
правой тройке векторов
, ![]() .
Для
левой тройки векторов
.
Для
левой тройки векторов ![]() Получаем,
Получаем, ![]() , где
, где ![]() –
объем параллелепипеда построенного на
векторах
,
,
.
–
объем параллелепипеда построенного на
векторах
,
,
.

Свойства смешанного произведения
1. Смешанное
произведение не меняется при циклической
перестановке его сомножителей (не
меняется ни объем параллелепипеда, ни
ориентация его ребер): ![]() .
.
2. Смешанное
произведение не меняется![]() знаков
векторного и скалярного умножения:
знаков
векторного и скалярного умножения:![]() , поэтому
смешанное произведение записывают
, поэтому
смешанное произведение записывают ![]() .
.
3. Смешанное
произведение меняет свой знак при
перемене любых двух вектор-сомножителей: ![]() ,
,![]() .
.
4. Смешанное
произведение ненулевых векторов
,
и
равно
нулю тогда и только тогда, когда они
компланарны: ![]() ,
,
–
компланарны
,
,
–
компланарны![]() .
.
Доказательство. Предположим,
что векторы
,
и
–
не компланарны. Тогда можно построить
параллелепипед имеющий объем ![]() ,
т.е.
,
т.е. ![]() ,
но это противоречит условию, согласно
которого,
,
но это противоречит условию, согласно
которого, ![]() .
Следовательно, векторы
,
и
–
компланарны.
.
Следовательно, векторы
,
и
–
компланарны.
Обратно,
пусть
,
и
–
компланарны. Тогда вектор ![]() и
перпендикулярен плоскости, в которой
находятся векторы
,
и
,
значит, он перпендикулярен любому
вектору, лежащему в этой плоскости,
например
и
перпендикулярен плоскости, в которой
находятся векторы
,
и
,
значит, он перпендикулярен любому
вектору, лежащему в этой плоскости,
например ![]() Это
значит, что
Это
значит, что ![]() .
.
43. Геометрический смысл скалярного, векторного и смешанного произведения.
Пусть ![]() и
и ![]() —
два ненулевых вектора. Если отложить
их от одной точки
—
два ненулевых вектора. Если отложить
их от одной точки ![]() ,
получится угол между
этими векторами (точнее между несущими
их полупрямыми, исходящими из точки
).
Этот угол обозначают
,
получится угол между
этими векторами (точнее между несущими
их полупрямыми, исходящими из точки
).
Этот угол обозначают ![]() .
.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
![]()
Если один из векторов нулевой, то угол не определен, и произведение считают равным нулю.
Геометрический смысл скалярного произведения
1)Связь с проекциями
Алгебраическое значение проекции вектора на вектор вдоль прямой, перпендикулярной , очевидно, равно
Аналогично
Таким образом, скалярное произведение
2)Связь с длинами
Рассмотрим скалярное произведение вектора на самого себя.
3)Связь с углами
Рассмотрим скалярное произведение единичных векторов. Поскольку их длины равны 1, то
Векторное произведение —это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов.
Геометрические свойства векторного произведения
Модуль
векторного произведения ![]() равняется
площади
равняется
площади ![]() параллелограмма,
построенного на приведённых к общему
началу векторах
и
(Если
параллелограмма,
построенного на приведённых к общему
началу векторах
и
(Если ![]() — единичный
вектор,
ортогональный векторам
и
и
выбранный так, что тройка
— единичный
вектор,
ортогональный векторам
и
и
выбранный так, что тройка ![]() —
правая, а
—
площадь параллелограмма, построенного
на них (приведённых к общему началу), то
для векторного произведения справедлива
формула:
—
правая, а
—
площадь параллелограмма, построенного
на них (приведённых к общему началу), то
для векторного произведения справедлива
формула:![]() При использовании векторного и скалярного
произведений можно высчитать объём
параллелепипеда, построенного на
приведённых к общему началу
векторах a, b и c.
Такое
произведение трех векторов
называется смешанным.
При использовании векторного и скалярного
произведений можно высчитать объём
параллелепипеда, построенного на
приведённых к общему началу
векторах a, b и c.
Такое
произведение трех векторов
называется смешанным.![]() Величина
векторного произведения зависит
от синуса угла
между изначальными векторами, поэтому
векторное произведение может восприниматься
как степень «перпендикулярности»
векторов также, как и скалярное
произведение может
рассматриваться как степень
«параллельности». Векторное произведение
двух единичных
векторов равно
1 (единичному вектору), если изначальные
векторы перпендикулярны, и равно 0
(нулевому вектору), если векторы
параллельны либо антипараллельны.
Смешанным
произведением трех векторов
,
,
называется
число
.
Геометрический
смысл смешанного произведения: модуль
смешанного произведения трех векторов
численно равен объему параллелепипеда,
построенного на этих векторах.Пусть
ребрами параллелограмма являются
векторы
,
,
образующие
правую тройку векторов и вектор
Величина
векторного произведения зависит
от синуса угла
между изначальными векторами, поэтому
векторное произведение может восприниматься
как степень «перпендикулярности»
векторов также, как и скалярное
произведение может
рассматриваться как степень
«параллельности». Векторное произведение
двух единичных
векторов равно
1 (единичному вектору), если изначальные
векторы перпендикулярны, и равно 0
(нулевому вектору), если векторы
параллельны либо антипараллельны.
Смешанным
произведением трех векторов
,
,
называется
число
.
Геометрический
смысл смешанного произведения: модуль
смешанного произведения трех векторов
численно равен объему параллелепипеда,
построенного на этих векторах.Пусть
ребрами параллелограмма являются
векторы
,
,
образующие
правую тройку векторов и вектор
Имеем ∙ , так как – площадь основания построенного на векторах , а – высота параллелограмма, то – объем параллелограмма построенного на правой тройке векторов , .
Для левой тройки векторов .
Получаем, , где – объем параллелепипеда построенного на векторах , , .
44.Аффинная система координат. Прямоугольная система координат?
Пусть в пространстве V3 (на плоскости V2 или на прямой V1) зафиксиоована некотороая точка О, называемая полюсом. Для любой точки А вектор rA = называется радиус - вектором точки А относительно полюса О. Задание точки ее радиус - вектором определяет, очевидно, биективное отображение. Тот факт, что точка А имеет радиус - вектор r, обозначают символом А(r). Если в пространстве V3 завиксираваны точка О и базис e1, e2, e3, то говорят, что в пространстве задана аффинная система координат (или общая декартова система координат) {O; e1, e2, e3}. Точка О называется началом координат; оси, проходящие через начало координат и определенные векторами e1, e2, e3, называются осями коордиеат и обозначаются Ох (ось абцисс), Оу (ось ординат), Oz (ось аппликат) соответственно. Плоскость, определяемая осями координат Ох и Оу (Ox и Oz, Oy и Oz), называется координатной плоскостью Oxy (Oxz, Oyz соответственно). В этой терминалогии аффинная система координат обозначается также символом Oxyz. Координатами точки А в аффинной системе координат {O; e1, e2, e3} называются координаты радиус - вектора rA этой точки в базисе e1, e2, e3. Тот факт, что точка А имеет координаты x, y, z, обозначают символом А( x, y, z). Итак,
rA = xe1 + ye2 + ze3 ⇔ A(x, y, z). 3.2.1
Замечание
1.Из
определения следует, что любая точка А
пространства в заданной системе координат
имеет координаты, причем точки A1(x1,
y1,
z1)
и A2(x2,
y2,
z2)
совпадают тогда и только тогда, когда
x1
= x2,
y1
= y2,
z1
= z2.
Замечание
2.Координаты
точки A(x, y, z) определяются соотношениями
(3.1.4)
. При этом, как легко видеть, проекции
A1,
A2,
A3
точки А имеют координаты A1(x,
0, 0), A2(0,
y, 0), A3(0,
0, z) .
Аналогично определяются аффинные
системы координат {O; e1,
e2}
на плоскости V2
и {O; e1}
на прямой V1,
а также координаты точки А(x, y) и A(x)
соответственно. При этом имеют место
очевидные аналоги соотношения (3.2.1) и
обоих замечаний. В дальнейшем все факты
будем излагать только в терминах V3.
Теорема 3.1Если
A(x1,
y1,
z1)
и B(x2,
y2,
z2)
− точки пространства, заданные своими
координатами в системе координат {O; e1,
e2,
e3},
то вектор а =
![]() в
базисе e1,
e2,
e3имеет
координаты а = {x2
= x1,
y2
= y1,
z2
= z1}.
Д
в
базисе e1,
e2,
e3имеет
координаты а = {x2
= x1,
y2
= y1,
z2
= z1}.
Д оказательство.
Действительно,
=
−
(рис.
1) и, следовательно, а = rB
− rA.
Так как rA
= {(x1,
y1,
z1},
rВ
= {(x2,
y2,
z2},
то в силу свойства линейности координат
отсюда следует утверждение теоремы.
Теорема
доказана.
Деление отрезка в данном
отношении. Гворят, что точка М ≠ В делит
отрезок [АВ] в отношении λ, если
оказательство.
Действительно,
=
−
(рис.
1) и, следовательно, а = rB
− rA.
Так как rA
= {(x1,
y1,
z1},
rВ
= {(x2,
y2,
z2},
то в силу свойства линейности координат
отсюда следует утверждение теоремы.
Теорема
доказана.
Деление отрезка в данном
отношении. Гворят, что точка М ≠ В делит
отрезок [АВ] в отношении λ, если
![]() =
λ
=
λ![]() (рис.
2).
(рис.
2).
 Обозначение:
(АВМ) = λ. Из определения следует, что
точка М расположена на прямой АВ, при
этом (рис. 2):
Обозначение:
(АВМ) = λ. Из определения следует, что
точка М расположена на прямой АВ, при
этом (рис. 2):
если М − внутренняя точка отрезка [AB], то λ > 0;
если М = А, то λ = 0;
если М расположена вне отрезка [AB], то λ < 0.
Заметим, что других вариантов расположения точки М не может быть и что в одном из возможных вариантов λ не равно -1. Теорема 3.2Пусть A(r1), B(r2), M(r3) − точки пространства и (АВМ) = λ. Тогда
![]() (3.2.2)
(3.2.2)
Доказательство. Условие (АВМ) = λ означает, что = λ или r3− r1 = λ(r2 −r3). Отсюда следует (3.2.2). Теорема доказана. Следствие.Соотношение (3.2.2) в координатной форме имеет следующий вид: для A(x1, y1, z1), B(x2, y2, z2), М(x3, y3, z3)
![]() (3.2.3)
(3.2.3)
Прямоугольные координаты. Базис e1, … ,en, где n = 1, 2, 3, называется ортонормированным, если векторы базиса
имеют единичную длину и, в случае n >1,
попарно перпендикулярны.
Аффинная система координат {O; e1, e2, e3}, соответствующая ортонормированному базису e1, e2, e3, называется прямоугольной декартовой системой координат.
45 Радиус Вектора Расстояние между двумя точками
Расстояние между точками |
Проведем
через точки ![]() и
и ![]() прямые,
параллельные оси z.
Пусть эти прямые пересекут плоскость xy в
точках
прямые,
параллельные оси z.
Пусть эти прямые пересекут плоскость xy в
точках ![]() и
и ![]() Заметим,
что поскольку эти точки лежат в
плоскости xy,
то координата z у
них равна нулю. Проведем плоскость через
точку
Заметим,
что поскольку эти точки лежат в
плоскости xy,
то координата z у
них равна нулю. Проведем плоскость через
точку ![]() параллельную
плоскости xy.
Пусть эта плоскость пересекает прямую
параллельную
плоскости xy.
Пусть эта плоскость пересекает прямую ![]() в
точке C.
Применим теорему Пифагора к
треугольнику
в
точке C.
Применим теорему Пифагора к
треугольнику ![]()
![]() Очевидно,
что отрезки
Очевидно,
что отрезки ![]() и
и ![]() равны,
а согласно теореме Пифагора на плоскостиxy,
получаем, что
равны,
а согласно теореме Пифагора на плоскостиxy,
получаем, что ![]() Поскольку
длина отрезка
Поскольку
длина отрезка ![]() равна
равна ![]() то
окончательно имеем
то
окончательно имеем ![]()
Если
же окажется, что отрезок ![]() параллелен
оси z,
то
параллелен
оси z,
то ![]() Но
тот же результат дает полученная формула,
так как в этом случае
Но
тот же результат дает полученная формула,
так как в этом случае ![]()
![]()
Итак, доказана следующая
Теорема 9.7.
Расстояние между точками A1 и A2 можно вычислить по формуле
|
Определение 9.14.
Вектор, конец которого совпадает с данной точкой, называется радиус-вектором данной точки.
Ра́диус-ве́ктор (обычно
обозначается ![]() или
просто
или
просто ![]() )
— вектор,
задающий положения точки в пространстве относительно
некоторой заранее фиксированной точки,
называемой началом координат.
)
— вектор,
задающий положения точки в пространстве относительно
некоторой заранее фиксированной точки,
называемой началом координат.
Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.
Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.
На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.
46 Уравнение прямой на плоскости
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Уравнение прямой по точке и вектору нормали
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
Пример.
Найти уравнение прямой, проходящей
через точку А(1, 2) перпендикулярно вектору
![]() (3,
-1).
(3,
-1).
Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой, проходящей через эти точки:

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:

если х 1 ≠ х2 и х = х 1 , если х 1 = х2 .
Дробь
 =
k называется угловым
коэффициентом прямой.
=
k называется угловым
коэффициентом прямой.
Уравнение прямой по точке и направляющему вектору
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.
Определение.
Каждый
ненулевой вектор
![]() (
α1
, α2
), компоненты которого удовлетворяют
условию А α1
+ В α2
= 0 называется направляющим вектором
прямой
(
α1
, α2
), компоненты которого удовлетворяют
условию А α1
+ В α2
= 0 называется направляющим вектором
прямой
Ах + Ву + С = 0.
Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).
Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0. при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:
х + у - 3 = 0
47 Нормальный и направляющий вектор на прямой
Всякое уравнение первой степени относительно координат x, y, z
Ax + By + Cz +D = 0 (3.1)
задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.
Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.
Особые случаи уравнения (3.1):
1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.
2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.
3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.
4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: x = 0, y = 0, z = 0.
Прямая в пространстве может быть задана:
1) как линия пересечения двух плоскостей,т.е. системой уравнений:
A 1 x + B 1 y + C 1 z + D 1 = 0, A 2 x + B 2 y + C 2 z + D 2 = 0; (3.2)
2) двумя своими точками M 1 (x 1, y 1, z 1 ) и M 2 (x 2, y 2, z 2 ), тогда прямая, через них проходящая, задается уравнениями:
![]() =
=
![]() ;
(3.3)
;
(3.3)
3) точкой M 1 (x 1, y 1, z 1 ), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:
![]() .
(3.4)
.
(3.4)
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор aназывается направляющим вектором прямой.
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:
x = x 1 + mt , y = y 1 + nt , z = z 1 + р t . (3.5)
Решая систему (3.2) как систему линейных уравнений относительно неизвестных xи y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой:
x = mz + a, y = nz + b. (3.6)
От уравнений (3.6) можно перейти к каноническим уравнениям, находя zиз каждого уравнения и приравнивая полученные значения:
![]() .
.
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [ n1, n2 ], где n1 (A 1, B 1, C 1 ) и n2 (A 2, B 2, C 2 ) - нормальные векторы заданных плоскостей. Если один из знаменателей m, nили р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система
![]()
равносильна
системе
![]() ;
такая прямая перпендикулярна к оси Ох.
;
такая прямая перпендикулярна к оси Ох.
Система
![]() равносильна
системе x = x 1,
y = y 1
; прямая параллельна оси Oz.
равносильна
системе x = x 1,
y = y 1
; прямая параллельна оси Oz.
48 Расположение двух прямых Условия параллельности и перпендикулярности прямых
Условие параллельности. Если прямые линии параллельны, то они наклонены к числовой оси ОХ под одним и тем же углом, следовательно, разница углов наклона параллельных прямых равна нулю (действительно они никогда не пересекаются). Тангенс угла в ноль градусов (ноль радиан) равен нулю. То есть левая часть уравнения (1-4) равна нулю, тогда нулю должна быть равна и правая часть данного выражения. Дробь равна нулю если числитель равен нулю. В нашем случае это может быть при:
k2 = k1. (1-5)
Это и есть условие параллельности двух прямых линий.
Условие перпендикулярности Если две прямых линии взаимно перпендикулярны, то угол между ними равен 90 или П/2 радиан. Тангенс такого угла не существует (иногда говорят, что он равен бесконечности). Правая часть (1-4) не существует при равенстве нулю знаменателя, т.е.
k2 * k1 = -1. (1-6)
Условие параллельности прямых заключается в равенстве их угловых коэффициентов. tgφ1=tgφ2 или k1=k2 Условие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1 k1k2=-1 Пример 7. Составить уравнение прямой линии, проходящей через точку (1;2) параллельно прямой 2х-3у+1=0. Решение.
Угловой коэффициент k прямой линии,
для которой нужно составить уравнение,
равен угловому коэффициенту |
Расположение двух прямых
Если
прямые заданы уравнениями ![]() и
и ![]() то
они:
то
они:
1)
параллельны (но не совпадают) ![]()
2)
совпадают ![]()
3)
пересекаются ![]()
4)
скрещиваются ![]()
Если ![]() то
случаи 1 - 4 имеют место, когда (
то
случаи 1 - 4 имеют место, когда (![]() -
знак отрицания условия):
-
знак отрицания условия):
1)
![]()
2)
![]()
3)

4)

49.Угол между двумя прямыми
Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x1; y1; z1) и b = (x2; y2; z2), то сможете найти угол. Точнее, косинус угла по формуле:
![]()
Посмотрим, как эта формула работает на конкретных примерах:
Задача. В кубе ABCDA1B1C1D1 отмечены точки E и F — середины ребер A1B1 и B1C1соответственно. Найдите угол между прямыми AE и BF.

Решение. Поскольку ребро куба не указано, положим AB = 1. Введем стандартную систему координат: начало в точке A, оси x, y, z направим вдоль AB, AD и AA1соответственно. Единичный отрезок равен AB = 1. Теперь найдем координаты направляющих векторов для наших прямых.
Найдем координаты вектора AE. Для этого нам потребуются точки A = (0; 0; 0) и E = (0,5; 0; 1). Поскольку точка E — середина отрезка A1B1, ее координаты равны среднему арифметическому координат концов. Заметим, что начало вектора AE совпадает с началом координат, поэтому AE = (0,5; 0; 1).
Теперь разберемся с вектором BF. Аналогично, разбираем точки B = (1; 0; 0) и F = (1; 0,5; 1), т.к. F — середина отрезка B1C1. Имеем: BF = (1 − 1; 0,5 − 0; 1 − 0) = (0; 0,5; 1).
Итак, направляющие векторы готовы. Косинус угла между прямыми — это косинус угла между направляющими векторами, поэтому имеем:
![]()
Ответ: arccos 0,8
50.Расстояние от точки до прямой
Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из точки на прямую. Если точка M0∈l , то ρ(M0,l)=0 (расстояние от точки M0 до прямой l) Для всякой точки M2/=M1 M0M2>M0M1
Найдем ρ(M0,l) - ? Oi→j→− прямоугольная система координат;
M0(x0,y0);M1(x1,y1);
−−−−−−−→M0M1⊥l и −→n⊥l ;
−−−−−−−→M0M1∣∣−→n , тогда
−−−−−−−→M0M1·−→n=∣ ∣ −−−−−−−→M0M11∣ ∣ ·∣−→n∣(±1)
−−−−−−−→M0M1(x1−x0,y1−y0);−→n(A,B);
−−−−−−−→M0M1·−→n=A(x1−x0)+B(y1−y0)=Ax1+By1−(Ax0+By0), т.к. M1(x1,y1)∈l⇒Ax1+By1+C=0 , следовательно, последнее выражение можно переписать в виде:
−−−−−−−→M0M1·−→n=A(x1−x0)+B(y1−y0)=−(С+Ax0+By0)
Длина вектора −−→∣n∣=√A2+B2 Подставим все в выражение (1): −(С+Ax0+By0)=±ρ(M0,l)√A2+B2
Откуда получим конечное выражение для нахождения расстояния от точки до прямой:
ρ(M0,l)=√A2+B2∣ ∣ Ax0+By0+С∣ ∣