
- •9. Вырожденные и невырожденные матрицы. Ранг матрицы. Теорема о ранге матрицы.
- •Уравнение плоскости по трем точкам:
- •4. Уравнение плоскости по точке и двум неколлинеарным векторам
- •Геометрический смысл предела числовой последовательности
- •Основные свойства сходящихся последовательностей
- •Арифметические действия над последовательностями, имеющими предел
- •1. Бесконечно малые функции при х
- •2. Предел функции при х и его свойства.
- •1. Бесконечно малые функции при х а
- •2. Предел функции в точке
- •3. Односторонние пределы
- •44 Вопрос. Глобальные свойства непрерывных функций.
- •Формула конечных приращений
- •Понятие дифференциала
- •Свойства дифференциала. Инвариантность формы дифференциала
- •51Производные основных элементарных функций
- •53 Вопрос. Логарифмическая производная. Производная функции u(X)V(X).
- •56 Вопрос. Направление вогнутости. Точки перегиба.
- •64 Вопрос. Частные производные и дифференциалы высших порядков. Матрица Гессе.
- •66 Экстремум функции нескольких переменных
- •Билет 70. Неопределенный интеграл. Простейшие свойства.
- •Для неопределённого интеграла
- •Для определённого
- •Метод замены переменной (метод подстановки)
- •72Интегрирование дробно-рациональных функций
44 Вопрос. Глобальные свойства непрерывных функций.
Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
Областью значений функции
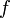 ,
непрерывной на отрезке
,
непрерывной на отрезке
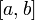 ,
является отрезок
,
является отрезок где
минимум и максимум берутся по отрезку
.
где
минимум и максимум берутся по отрезку
.(Теорема о существовании корня) Если функция непрерывна на отрезке и
 то
существует точка
то
существует точка
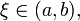 в
которой
в
которой
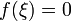 .
.Если функция непрерывна на отрезке и число удовлетворяет неравенству
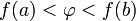 или
неравенству
или
неравенству
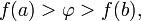 то
существует точка
в
которой
то
существует точка
в
которой
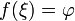 .
.Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
Монотонная функция на отрезке непрерывна в том и только в том случае, когда область ее значений является отрезком с концами
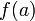 и
и
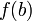 .
.Если функции и
 непрерывны
на отрезке
,
причем
непрерывны
на отрезке
,
причем
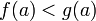 и
и
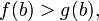 то
существует точка
в
которой
то
существует точка
в
которой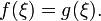 Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
Билет 45. Следствия из числа е.
1) lim((1+)*1/=e – прологарифмируем данное уравнение по основанию а:
loga lim(1+*1/=logae
Логарифмическая функция непрерывна в своей области определения , поэтому :
limloga(1+)*1/=logae
2) lim ( loga(1+)/=logae частный случай a=e.
3) lim((ln(1+)/=1
4) lim (a*-1)/=lna – 2-ое следствие.
5) lim(e*-1)/=1, a=e.
6) lim((1+)*-1)/= (-const) ln(1+)=ln(1+)
Число е. Задача о непрерывном начислении процентов.
1) Числом е называется предел : lim(n)*(1+1/n)*n=lim(n)(1+1/n)*n=lim(0)(1+)*1/=e.
Это число иррационально и приближенно = 2,71828. Логарифмы с основанием е называется натуральными и обозначается logex=ln x.
2) В банках процентные деньги присоединяются к основному капиталу ежегодно, если присоединяются чаще, то капитал растет быстрее. П-Р: в банк положено 100 руб. из расчета 100 % годовых.
Если проц. деньги будут присоединены к основному капиталу по истечении года, то 100 р. превратятся в 200 р.
Если проц. деньги присоединять к основному капиталу каждые полгода, то 100 руб. вырастут в 100 1,5 = 150, а еще через полгода - в 150 1,5 = 225.
Если присоединены каждые 1/3 года, то по истечении года будет 100 (1 +1/3) 237.
Учащая сроки присоединения проц. денег до 0,1 года, до 0,01 года, до 0,001 года и т.д, то 100 (1 +1/10)10 259 , 100 (1+1/100)100 270, 100 (1+1/1000)1000 271 наращенный капитал приближается к н-рому пределу, = приблизительно 271.
Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиваться не может, даже если бы наросшие % присоединялись каждую сек, т.к: е = .
Билет 46. Асимптоты.
При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой. Понятие асимптоты играет важную роль в математическом анализе. Они проводятся при изучении свойств многих кривых (гиперболы, конхоиды, логарифмич. линии, циссоиды и др.).
Асимптотой графика функции у=f(x) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Прямая
x =
a называется
вертикальной
асимптотой графика
функции f (
x )
при x →
a,
если выполнено хотя бы одно из условий
![]() ,
,
![]()
![]() Если
предел функции f(x)=a,
то прямая у = а называется горизонтальной
асимптотой.
Если
предел функции f(x)=a,
то прямая у = а называется горизонтальной
асимптотой.
.
Наклонная
асимптота — прямая
вида
![]() при
условии существования пределов
при
условии существования пределов
Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!
Замечание: Если
хотя бы один из двух упомянутых выше
пределов не существует (или равен
![]() ),
то наклонной асимптоты при
),
то наклонной асимптоты при
![]() (или
(или
![]() )
не существует!
)
не существует!
горизонтальная
асимптота является частным случаем
наклонной
при
![]()
Применение пределов в экономических расчетах
Сложные проценты В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за фиксированные одинаковые интервалы времени (год, полугодие, квартал и т. д.). Время - дискретная переменная. В некоторых случаях - в доказательствах и расчетах, связанных с непрерывными процессами, возникает необходимость в применении непрерывных процентовПотоки платежей. Финансовая рента Контракты, сделки, коммерческие и производственно-хозяйственные операции часто предусматривают не отдельные разовые платежи, а множество распределенных во времени выплат и поступлений. Отдельные элементы такого ряда, а иногда и сам ряд платежей в целом, называется потоком платежей. Члены потока платежей могут быть как положительными (поступления), так и отрицательными (выплаты) величинами.
Производная, правила и формулы дифференцирования На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.
Пусть
мы нашли для функции y=f(x) ее производную
y ¢ = f ¢ (x). Производная от этой производной
называется производной
второго порядка функции
f(x), или второй
производной, и
обозначается ![]() ,
u=x 4 +1.
Замена переменной; интегрирование
по частям Справочный
материал и примеры к выполнению
контрольной работы по математике
,
u=x 4 +1.
Замена переменной; интегрирование
по частям Справочный
материал и примеры к выполнению
контрольной работы по математике
Предельный анализ в экономике - совокупность приемов исследования изменяющихся величин затрат или результатов при изменении объемов производства, потребления и т.п. на основе анализа их предельных значений. Большей частью плановые расчеты, основывающиеся на обычных статистических данных, ведутся в форме суммарных показателей. При этом анализ заключается главным образом в вычислении средних величин. Нахождение производительности труда
Экстремум функции Функция y=f ( x ) называется возрастающей ( убывающей ) в некотором интервале, если при x 1 < x 2 выполняется неравенство f (x 1 ) < f (x 2 ) ( f (x 1 ) > f (x 2 )). Пример . Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Раскрытие неопределенностей. Правило Лопиталя
Частные
производные.
Метод наименьших квадратов В экономике
рассматриваются функции не только от
двух, но и большего
числа независимых переменных. Например,
уровень рентабельности R зависит от
прибыли П на реализованную продукцию,
величин основных ( a ) и оборотных ( b )
фондов, R = П/( a+b ), т.е. R является функцией
трех независимых переменных R = f (П, a , b
). Частными
производными второго порядка функции z
= f ( x , y ) называются частные производные
от ее частных производных первого
порядка. Если первая производная была
взята, например, по аргументу x ,
то вторые производные обозначаются
символами![]() d tdt
, а современная величина платежа P = S ex
(-
d tdt
, а современная величина платежа P = S ex
(- ![]() ,
,
и пусть, кроме того, дефицит в расходах правительства прямо пропорционален доходу Y (при коэффициенте пропорциональности q ). Решить уравнение y ¢¢¢ = cos x. Решить уравнение y ¢¢ - y = 0.
Решение. Характеристическое уравнение имеет вид k 2 - 1 = 0, корни которого k 1 = 1, k 2 = -1 действительны и различны.
Разностные уравнения На практике простейшие разностные уравнения возникают при исследовании например величины банковского вклада. Эта величина является переменной Y x , представляющей сумму, которая накапливается по установленному закону при целочисленных значениях аргумента x . Пусть сумма Y o положена в банк при условии начисления 100 r сложных процентов в год. Пусть начисление процентов производится один раз в год и x обозначает число лет с момента помещения вклада ( x = 0, 1, 2,...). Обозначим величину вклада по истечении x лет через Y x . Обыкновенным разностным уравнением называется уравнение, связывающее значения одного независимого аргумента x , его функции Y x и разностей различных порядков этой функции D Y x , D 2 Y x, D 3 Y x,.... Такое уравнение можно записать в общем виде следующим образом:j ( x , Y x , D Y x , D 2 Y x D 3 Y x, D n Y x ) = 0, (10.1)
Производная функции
y = f ( x ) может также обозначаться одним
из следующих способов: ![]()
![]()
![]() В
физике производную
по времени t часто обозначают точкой:
В
физике производную
по времени t часто обозначают точкой: ![]()
Билет 48. Производная. Геометрический, механический и экономический смысл производной. Эластичность функций.
Производной функции y=f(x) в точке х называется предел lim(xo)(f(x+x)f(x))/x=lim(xo)(y/x).
Если этот предел конечный, то функция называется дефферинцируемой в точке х, при этом она оказывается обязательно и непрерывной в этой точке. Если предел равен + или -, то ф-ия f(x) имеет в точке х бесконечную производную.
Нахождение производной – дифференцирование функции.
Геометрический смысл: это угловой коэффициент касательной к данной точке.
Механический смысл: производная от пути по времени личная скорость.
Экономический смысл: производная, вычисленная от кол-ва произведённой продукции в данный момент времени есть производительность труда.
Эластичностью функции называется Ex(y) предел отношения относительного приращения к относительному приращению переменной х при хо: Ex(y)=lim(xo)(y/y:x/x)=lim(xo)(y umn x/y umn x)=x/ylim(xo)(y/x)=x/y umn y’ Ex(y)=x/y umn y’
Эластичность функции показывает приближённо насколько процентов изменяется функция у при изменении независимой переменной х на 1%. Если Ex(y)<1 – спрос не эластичен, Ex(y)>1 – спрос эластичен. Ex(y)=1 –cпрос нейтральный
Формула для приращения функции. Дифференциал функции.
Формула малых приращений
Подставив (2) в (1) и отбросив ω(x - x0), получаем формулу малых приращений:
Δf(x0) ≈ df(x0)
или
f(x) ≈ f(x0) + f'(x0)(x - x0), (4)
позволяющую при малых значениях x - x0 приближенно вычислять значения функции f в точках x, близких к точке x0, где значения функции f и ее производной известны.
